Cho tam giác ABC cân (AB = AC). Các đường phân giác BE, CF cắt nhau tại H.
a) Chứng minh
b) Tia AH cắt BC tại D. Chứng minh D là trung điểm của BC và EF // BC.
c) Chứng minh AH là trung trực của EF. So sánh HF và HC.
 Giải bởi Vietjack
Giải bởi Vietjack
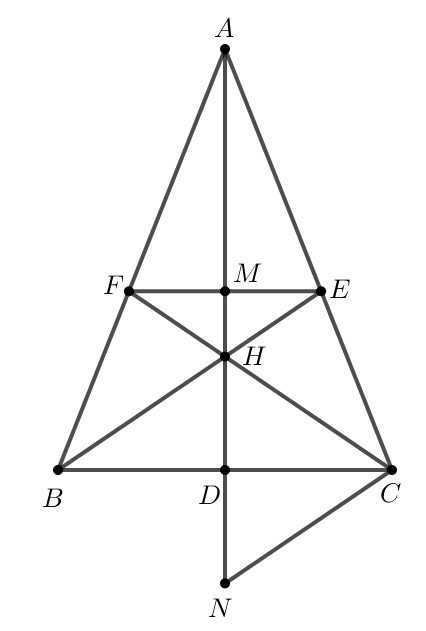
a) Do cân tại A nên AB = AC và
Do BE là tia phân giác của nên
Do CF là tia phân giác của nên
Do đó
Xét và có:
chung
AB = AC (chứng minh trên)
(chứng minh trên)
b) Do hai đường phân giác BE và CF của cắt nhau tại H nên AH là đường phân giác của hay AD là đường phân giác của
Tam giác ABC cân tại A có AD là đường phân giác của góc BAC nên AD vừa là đường phân giác, vừa là đường trung trực của tam giác ABC.
Do đó D là trung điểm của BC.
Do Tam giác ABE= tam giác ACF nên AE = AF (2 cạnh tương ứng).
Tam giác AEF có AE = AF nên Tam giác AEF cân tại A.
Do đó Góc AEF = góc AFE.
Xét trong Tam giác ABC: Góc ABC+ góc ACB+ góc BAC=180 độ
Mà góc ABC= góc ACB nên 2 góc ACB+ góc BAC=180 độ
(1).
Xét trong :
Mà nên
(2).
Từ (1) và (2) suy ra
Mà hai góc này ở vị trí đồng vị nên EF // BC.
c) Gọi M là giao điểm của AH và EF.
Do AH là đường phân giác của nên AM là đường phân giác của .
cân tại A, có AM là đường phân giác nên AM vừa là đường phân giác, vừa là đường trung trực của .
Do đó AM là đường trung trực của EF hay AH là đường trung trực của EF.
Do BE là đường phân giác của nên .
Do CF là đường phân giác của nên
Mà nên .
có nên cân tại H.
Do đó HB = HC.
Ta có là góc ngoài tại đỉnh F của nên .
Do đó .
Do nên .
Do đó .
Cho đơn thức A =
a) Thu gọn đơn thức A.
b) Xác định hệ số và bậc của đơn thức.
Thời gian giải một bài toán (tính theo phút) của 30 học sinh được ghi lại trong bảng dưới đây:
|
8 |
5 |
7 |
8 |
9 |
7 |
8 |
9 |
12 |
8 |
|
6 |
7 |
7 |
7 |
9 |
8 |
7 |
6 |
12 |
8 |
|
8 |
7 |
7 |
9 |
9 |
7 |
9 |
6 |
5 |
12 |
a) Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b) Lập bảng “tần số”.
c) Tính số trung bình cộng (làm tròn một chữ số thập phân) và mốt của dấu hiệu.
Cho đa thức f(x) thỏa mãn f(x) + x.f(-x) = x + 1 với mọi giá trị của x. Tính f(1).
Cho hai đa thức f(x) = 5 + 3x2 - x - 2x2 và g(x) = 3x + 3 - x - x2.
a) Thu gọn và sắp xếp hai đa thức theo lũy thừa giảm dần của biến.
b) Tính h(x) = f(x) + g(x).