Rút gọn biểu thức , ( giả sử tất cả các điều kiện đều được thỏa mãn ) ta được kết quả là
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D.
Ta có
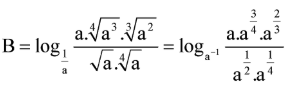
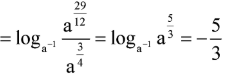
Cho a, b, c, d là các số nguyên dương, a khác 1, c khác 1 thỏa mãn và a-c=9. Khi đó b – d bằng