Cho hình vẽ sau:
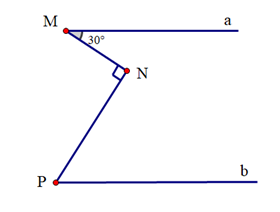
Biết Ma // Pb; MN ⊥ NP; \(\widehat {NMa}\) = 30°. Tính \(\widehat {NPb}\)
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
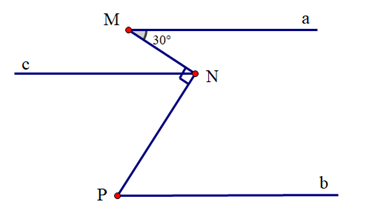
Kẻ Nc // Ma
Suy ra \(\widehat {MNc} = \widehat {NMa} = 30^\circ \) (hai góc so le trong)
Ta có \(\widehat {MNP} = \widehat {MNc} + \widehat {cNP}\) (hai góc kề nhau)
Suy ra \(\widehat {cNP} = \widehat {MNP} - \widehat {MNc}\)
Mà \(\widehat {MNP} = 90^\circ \) (do MN ⊥ NP)
Suy ra \(\widehat {cNP} = 90^\circ - 30^\circ = 60^\circ \)
Ta có Nc // Ma, mà Ma // Pb
Suy ra Nc // Pb (vì cùng song song với Ma)
Suy ra \(\widehat {NPb} = \widehat {cNP} = 60^\circ \) (hai góc so le trong)
Vậy \(\widehat {NPb} = 60^\circ \)
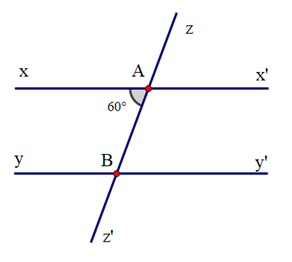
Cho hình vẽ:
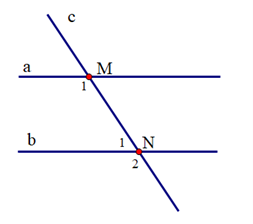
Biết a // b và \({\widehat M_1} - {\widehat N_1} = {100^o}\). Tính số đo các góc \({\widehat M_1},{\widehat N_1}\)
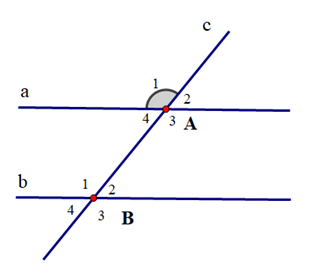
Cho hình vẽ, biết a // b và \({\widehat A_1} = {135^o}\). Số đo \({\widehat B_2}\) là:
Cho hình vẽ, biết x // y và \({\widehat M_2} = {70^o}\)
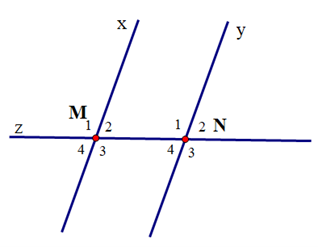
Số đo các góc \({\widehat N_1};{\widehat N_4}\) lần lượt là:
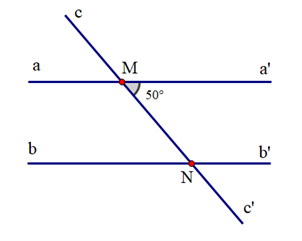
Cho hình vẽ:
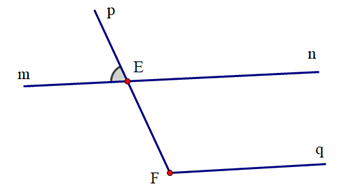
Biết mn // Fq và \(\widehat {pEm} = {79^o}\). Số đo \(\widehat {EFq}\) là:
Cho hình vẽ sau:
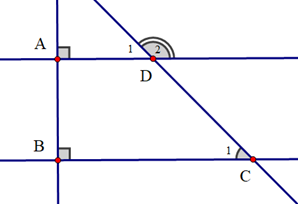
Biết \({\widehat C_1} = 45^\circ \). Số đo \({\widehat D_2}\) là: