Trắc nghiệm Toán 7 KNTT Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song có đáp án
Trắc nghiệm Toán 7 KNTT Dạng 2. Tính số đo các góc dựa vào tính chất hai đường thẳng song song có đáp án
-
426 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Hướng dẫn giải:
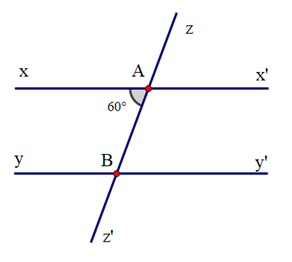
+ Ta có xx’ // yy’, suy ra \(\widehat {xAB} = \widehat {ABy'}\) (hai góc so le trong)
Suy ra \(\widehat {ABy'} = {60^o}\).
+ Ta có xx’ // yy’, suy ra \(\widehat {xAB} = \widehat {yBz'}\) (hai góc đồng vị)
Suy ra \(\widehat {yBz'} = {60^o}\).
+ Ta có \(\widehat {ABy}\) và \(\widehat {ABy'}\) là hai góc kề bù nên \(\widehat {ABy}\) + \(\widehat {ABy'}\) = 180°
Suy ra \(\widehat {ABy} = {180^o} - \widehat {ABy'} = {180^o} - {60^o} = {120^o}\).
Câu 2:
Cho hình vẽ sau:
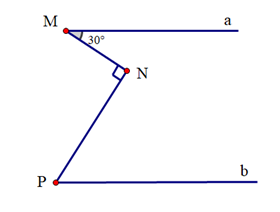
Biết Ma // Pb; MN ⊥ NP; \(\widehat {NMa}\) = 30°. Tính \(\widehat {NPb}\)
Xem đáp án
Hướng dẫn giải:
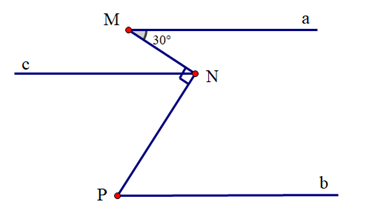
Kẻ Nc // Ma
Suy ra \(\widehat {MNc} = \widehat {NMa} = 30^\circ \) (hai góc so le trong)
Ta có \(\widehat {MNP} = \widehat {MNc} + \widehat {cNP}\) (hai góc kề nhau)
Suy ra \(\widehat {cNP} = \widehat {MNP} - \widehat {MNc}\)
Mà \(\widehat {MNP} = 90^\circ \) (do MN ⊥ NP)
Suy ra \(\widehat {cNP} = 90^\circ - 30^\circ = 60^\circ \)
Ta có Nc // Ma, mà Ma // Pb
Suy ra Nc // Pb (vì cùng song song với Ma)
Suy ra \(\widehat {NPb} = \widehat {cNP} = 60^\circ \) (hai góc so le trong)
Vậy \(\widehat {NPb} = 60^\circ \)
Câu 3:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
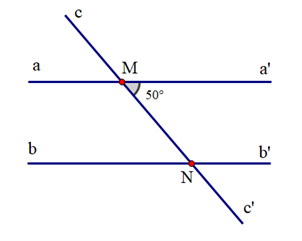
Ta có aa’ // bb’, suy ra \(\widehat {a'MN} = \widehat {MNb}\) (hai góc so le trong)
Vậy \(\widehat {MNb} = {50^o}\).
Câu 4:
Cho hình vẽ, biết a // b và \({\widehat A_1} = {135^o}\). Số đo \({\widehat B_2}\) là:
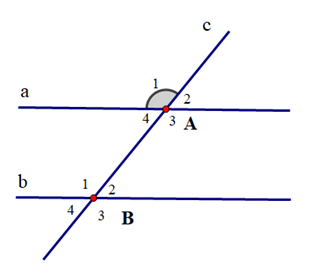
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Vì \({\widehat A_1}\) và \({\widehat A_2}\) là hai góc kề bù
Suy ra \({\widehat A_1} + {\widehat A_2} = 180^\circ \)(tính chất hai góc kề bù)
Suy ra \[{\widehat A_2}\; = 180^\circ - {\widehat A_1}\; = 180^\circ - 135^\circ \; = 45^\circ \]
Ta có a // b nên \({\widehat A_2} = {\widehat B_2}\) (hai góc đồng vị)
Suy ra \({\widehat B_2} = 45^\circ .\)
Câu 5:
Cho hình vẽ, biết x // y và \({\widehat M_2} = {70^o}\)
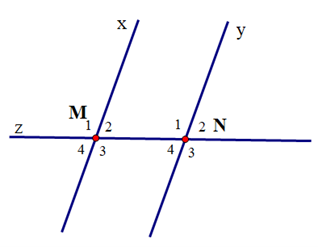
Số đo các góc \({\widehat N_1};{\widehat N_4}\) lần lượt là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Ta có x // y nên \({\widehat M_2} = {\widehat N_4}\) (hai góc so le trong)
Suy ra \({\widehat N_4} = 70^\circ \).
Mà \({\widehat N_1}\) và \({\widehat N_4}\) là hai góc kề bù nên \({\widehat N_1} + {\widehat N_4} = 180^\circ \) (tính chất hai góc kề bù)
Suy ra \({\widehat N_1} = 180^\circ - {\widehat N_4} = 180^\circ - 70^\circ = 110^\circ \)
Vậy ta chọn phương án D.
Câu 6:
Cho hình vẽ:
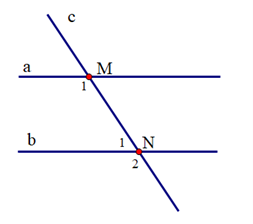
Biết a // b và \({\widehat M_1} - {\widehat N_1} = {100^o}\). Tính số đo các góc \({\widehat M_1},{\widehat N_1}\)
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Vì a // b nên \({\widehat M_1} = {\widehat N_2}\) (Hai góc đồng vị)
Mà \({\widehat N_1} + {\widehat N_2} = 180^\circ \) (Tính chất hai góc kề bù)
Suy ra \({\widehat N_1} + {\widehat M_1} = 180^\circ \)
Suy ra \({\widehat N_1} = {180^o} - {\widehat M_1}\)
Ta lại có \({\widehat M_1} - {\widehat N_1} = 100^\circ \)
Suy ra \({\widehat M_1} - ({180^o} - {\widehat M_1}) = 100^\circ \)
Suy ra \({\widehat M_1} - {180^o} + {\widehat M_1} = 100^\circ \)
Do đó \(2{\widehat M_1} = 280^\circ \)
Suy ra \({\widehat M_1} = 140^\circ \)
Do đó \({\widehat N_1} = {180^o} - {\widehat M_1} = 180^\circ - 140^\circ = 40^\circ \)
Vậy ta chọn phương án B.
Câu 7:
Cho hình vẽ sau:
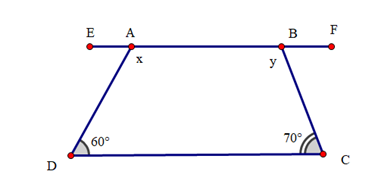
Biết AB // CD. Giá trị của x và y lần lượt là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
+ Vì AB // CD nên \(\widehat {ADC} = \widehat {EAD} = 60^\circ \) (hai góc so le trong)
Mà \(\widehat {EAD}\) và \(\widehat {DAB}\) là hai góc kề bù
Suy ra \(\widehat {EAD} + \widehat {DAB} = 180^\circ \) (tính chất hai góc kề bù)
Hay 60° + x = 180°
Suy ra x = 180° – 60° = 120°.
+ Vì AB // CD nên \(\widehat {FBC} = \widehat {BCD} = {70^o}\) (hai góc so le trong)
Mà \(\widehat {ABC}\) và \(\widehat {FBC}\) là hai góc kề bù
Suy ra \(\widehat {ABC} + \widehat {FBC} = 180^\circ \) (tính chất hai góc kề bù)
Hay y + 70° = 180°
Suy ra y = 180° – 70° = 110°.
Vậy ta chọn phương án B.
Câu 8:
Cho hình vẽ sau:
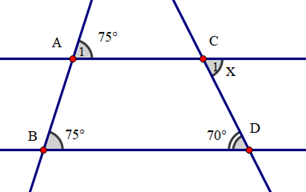
Giá trị của x là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Ta có \({\widehat A_1} = \widehat {ABD}\) (cùng bằng 75°)
Mà hai góc trên ở vị trí đồng vị.
Do đó AC // BD.
Suy ra \({\widehat C_1} = \widehat {CDB}\) (hai góc so le trong)
Hay x = 70°.
Vậy ta chọn phương án D.
Câu 9:
Cho hình vẽ sau:
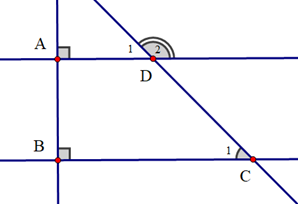
Biết \({\widehat C_1} = 45^\circ \). Số đo \({\widehat D_2}\) là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Vì hai đường thẳng AD và BC cùng vuông góc với đường thẳng AB nên AD // BC
Suy ra \({\widehat C_1} = {\widehat D_1} = 45^\circ \) (hai góc đồng vị)
Vì \({\widehat D_1};{\widehat D_2}\) là hai góc kề bù nên \({\widehat D_1} + {\widehat D_2} = 180^\circ \) (tính chất hai góc kề bù)
Suy ra \({\widehat D_2} = 180^\circ - {\widehat D_1} = 180^\circ - 45^\circ = 135^\circ \)
Vậy ta chọn phương án C.
Câu 10:
Cho hình vẽ:
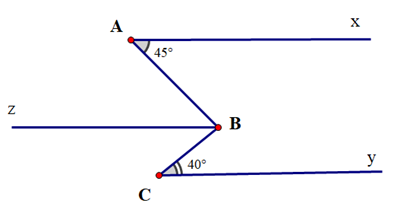
Biết Ax // Bz // Cy. Tính số đo \(\widehat {ABC}\)
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Vì Ax // Bz nên \(\widehat {xAB} = \widehat {ABz} = {45^o}\) (hai góc so le trong)
Vì Bz // Cy nên \(\widehat {zBC} = \widehat {BCy} = {40^o}\) (hai góc so le trong)
Ta có: \(\widehat {ABC}\) = \(\widehat {ABz}\) + \(\widehat {BCz}\) = 45° + 40° = 85°
Vậy ta chọn phương án A.
Câu 11:
Cho hình vẽ:
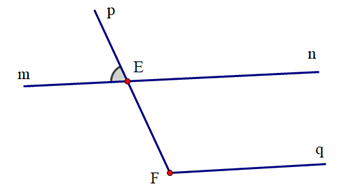
Biết mn // Fq và \(\widehat {pEm} = {79^o}\). Số đo \(\widehat {EFq}\) là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Vì \(\widehat {pEm}\) và \(\widehat {pEn}\) là hai góc kề bù nên:
\(\widehat {pEm}\) + \(\widehat {pEn}\) = 180° (tính chất hai góc kề bù)
Suy ra \(\widehat {pEn} = 180^\circ - \widehat {pEm} = 180^\circ - 79^\circ = 101^\circ \)
Vì mn // Fq nên suy ra \(\widehat {EFq} = \widehat {pEn}\)(hai góc đồng vị)
Do đó \(\widehat {EFq} = 101^\circ \).
Vậy ta chọn phương án A.
Câu 12:
Cho hình vẽ:
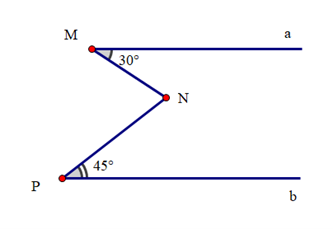
Biết Ma // Pb. Số đo \(\widehat {MNP}\) là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
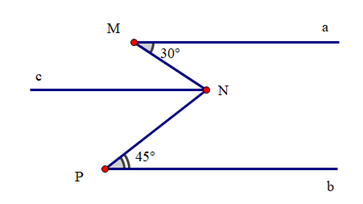
Kẻ Nc // Ma
Suy ra \(\widehat {aMN} = \widehat {MNc} = 30^\circ \)(hai góc so le trong)
Ta có Nc // Ma, mà Ma // Pb
Suy ra Pb // Nc (vì cùng song song với Ma)
Suy ra \(\widehat {NPb} = \widehat {cNP} = 45^\circ \) (hai góc so le trong)
Ta có \(\widehat {MNP} = \widehat {MNc} + \widehat {cNP}\) = 30° + 45° = 75°
Vậy ta chọn phương án C.