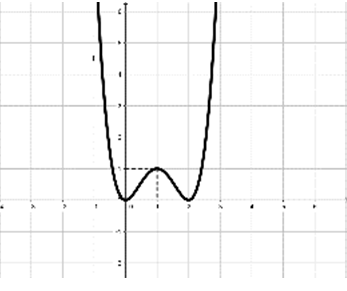
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên.
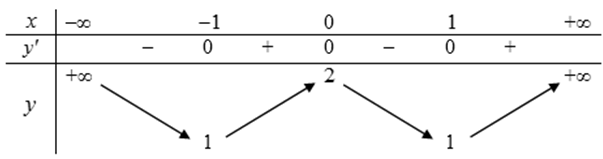
A. Hàm số đồng biến trên các khoảng (-1;0) và (1;+∞)
B. f (1) và f(-1) được gọi là giá trị cực tiểu của hàm số
C. x0 = 1 được gọi là điểm cực tiểu của hàm số
D. M(0;2) được gọi là điểm cực đại của hàm số
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D.
* Hàm số đồng biến trên (-1;0) và (1;+∞) => A đúng.
* x = -1; x = 1 là các điểm cực tiểu của hàm số, f(-1); f(1) là các giá trị cực tiểu của hàm số => B,C đúng.
* M(0;2) được gọi là điểm cực tiểu của đồ thị hàm số => D sai
Cho hàm số y = x4 – 2x2 – 1. Tìm số giao điểm của đồ thị hàm số với trục Ox:
Số giao điểm của trục hoành và đồ thị hàm số y = -x4 + 2x2 + 3 là:
Cho hàm số y = x4 – 4x2 – 2 có đồ thị (C) và đồ thị (P) : y = 1- x2. Số giao điểm của (P) và đồ thị (C) là
Đồ thị của hàm số y = -x3 + 3x2 + 2x – 1 và đồ thị của hàm số y = 3x2 – 2x – 1 có tất cả bao nhiêu điểm chung?
Tìm số giao điểm của đồ thị (C): y = x3 + x – 2 và đường thẳng y = x – 1
Tìm số giao điểm của đồ thị hàm số y = x4 – 2x2 và đồ thị hàm số y = x2 – 2
Tìm số giao điểm của đồ thị hàm số y = (x – 2)(x2 + x + 1) và trục hoành.
Tọa độ giao điểm có hoành độ nhỏ hơn 1 của đường (C): và đường thẳng (d): y = x + 1 là:
Cho hàm số y = f(x) xác định, liên tục trên R và có đồ thị là đường cong trong hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
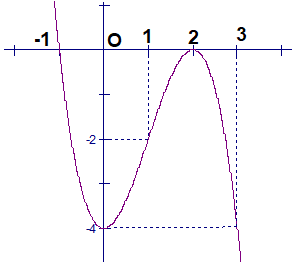
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên
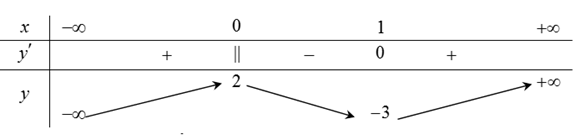
Khẳng định nào sau đây là khẳng định đúng
Đường cong hình bên là đồ thị của một hàm số nào trong bốn hàm số dưới đây