Cho hình chóp SABC có Gọi I là hình chiếu vuông góc của S lên mặt phẳng (ABC) Chọn khẳng định đúng trong các khẳng định sau.
A. I là trực tâm của .
C. I là tâm đường tròn ngoại tiếp của .
 Giải bởi Vietjack
Giải bởi Vietjack
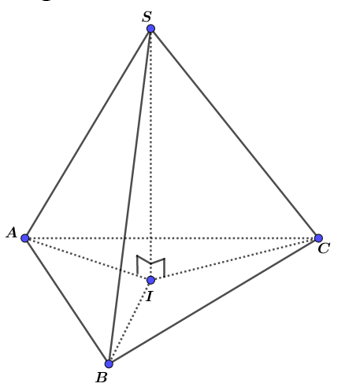
Ta có là các tam giác vuông tại I vì .
Xét vuông tại I và vuông tại I có: SI là cạnh chung, cạnh huyền SA=SB (cạnh huyền – cạnh góc vuông) (1).
Tương tự ta có (2).
Từ (1), (2) ta có . Vậy I là tâm đường tròn ngoại tiếp của .
Cho cấp số nhân có và . Tính tổng 1000 số hạng đầu tiên của cấp số nhân đã cho.
Cho hình vuông ABCD có cạnh bằng a Người ta dựng hình vuông có cạnh bằng đường chéo của hình vuông ABCD; dựng hình vuông có cạnh bằng đường chéo của hình vuông và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích S của tất cả các hình vuông bằng 8 thì a bằng:
Cho hàm số f(x) xác định trên R thỏa mãn . Giới hạn bằng
Cho tứ diện ABCD có , các cạnh còn lại bằng nhau và bằng 4 Mặt phẳng (P) chứa cạnh AB và vuông góc với cạnh CD tại I Diện tích tam giác IAB lớn nhất bằng:
Trong không gian cho ba đường thẳng phân biệt a,b,c Khẳng định nào sau đây đúng?
Cho các hàm số Có bao nhiêu hàm số trong các hàm số đã cho liên tục trên ![]() ?
?
Cho hàm số . Biết a là giá trị để hàm số liên tục tại điểm . Tìm số nghiệm nguyên của bất phương trình
Biết ba số theo thứ tự lập thành cấp số nhân. Giá trị của x bằng