Có bao nhiêu số nguyên n thỏa mãn \[(2n - 1) \vdots (n + 1)\;?\]
Giải bởi Vietjack
Trả lời:
Ta có
\[2n - 1 = 2n + 2 - 3 = (2n + 2) - 3 = 2(n + 1) - 3\]
Vì \[\left( {2n - 1} \right) \vdots \left( {n + 1} \right)\] nên \[\left[ {2\left( {n + 1} \right) - 3} \right] \vdots \left( {n + 1} \right)\]
Mà \[2\left( {n + 1} \right) \vdots \left( {n + 1} \right)\] suy ra \[ - 3 \vdots \left( {n + 1} \right) \Rightarrow n + 1 \in U\left( { - 3} \right) = \left\{ { \pm 1;\, \pm 3} \right\}\]
Ta có bảng sau:
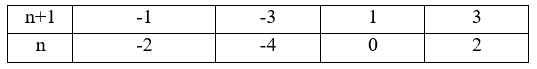
Vậy \[n \in \left\{ { - 4;\, - 2;\,0;\,2} \right\}\]
Do đó có 4 số nguyên nn thỏa mãn đề bài.
Đáp án cần chọn là: D
Cho \[E = \left\{ {3; - 8;0} \right\}\;\] . Tập hợp F gồm các phần tử của E và các số đối của chúng là?
Tìm giá trị lớn nhất của biểu thức : \[C = - {\left( {x - 5} \right)^2} + 10\]
Tính \[ - 4.[12:{( - 2)^2} - 4.( - 3)] - {( - 12)^2}\] ta được kết quả
Cho x là số nguyên và \[x + 1\;\] là ước của 5 thì giá trị của x là:
Cho \[x \in \mathbb{Z}\;\] và −5 là bội của \[x + 2\;\] thì giá trị của x bằng:
Cho các số sau: 1280;−291;43;−52;28;1;0 . Các số đã cho sắp xếp theo thứ tự giảm dần là:
Cho \({x_1}\) là số nguyên thỏa mãn \[{(x + 3)^3}:3 - 1 = - 10\] . Chọn câu đúng.
Bỏ ngoặc rồi tính: \[\left( {52 - 69 + 17} \right) - \left( {52 + 17} \right)\;\] ta được kết quả là
Thực hiện phép tính \[ - 567 - \left( { - 113} \right) + \left( { - 69} \right) - \left( {113 - 567} \right)\] ta được kết quả là
Tính \[\left( { - 9} \right).\left( { - 12} \right) - \left( { - 13} \right).6\]
