Cho góc nhọn . Trên tia Ax lấy hai điểm B và E, trên tia Ay lấy hai điểm D và C sao cho AB = AD, AE = AC. Gọi O là giao điểm của DE và BC. Cho OC = 1,5 cm, OD = 1cm. Độ dài đoạn thẳng DE là:
A. DE = 1,5 cm;
B. DE = 3 cm;
C. DE = 0,5 cm;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
⦁ Xét ∆ABC và ∆ADE, có:
AB = AD (giả thiết)
là góc chung.
AC = AE (giả thiết)
Do đó ∆ABC = ∆ADE (c.g.c)
⇒ và (2 góc tương tứng)
Ta có: (các cặp góc kề bù)
⇒
Ta lại có: DC = AC – AD, BE = AE – AB
Mà AC = AE, AB = AD nên DC = BE
⦁ Xét ∆DOC và ∆BOE, có:
(chứng minh trên)
DC = BE (chứng minh trên)
(chứng minh trên)
Do đó ∆DOC = ∆BOE (g.c.g)
⇒ OC = OE = 1,5cm
⇒ DE = OD + OE = 1 + 1,5 = 2,5 cm.
Vậy ta chọn phương án D.
Cho đoạn thẳng AB, điểm O nằm giữa A và B. Kẻ tia Ox vuông góc với AB. Trên tia Ox lấy các điểm C và D sao cho OC = OA, OD = OB. Gọi M, N lần lượt là trung điểm của AD và BC. Góc MON là:
Cho bốn điểm A, B, C, D thuộc đường tròn (O) sao cho AB = CD. Khẳng định nào sau đây sai?
Cho ∆MNP. Các đường phân giác trong các cắt nhau tại I. Kết luận nào sau đây đúng?
Cho tam giác ABC, có AB = 2,BC = 7, AC = . Lấy M là trung điểm của AB, N là trung điểm của AC.
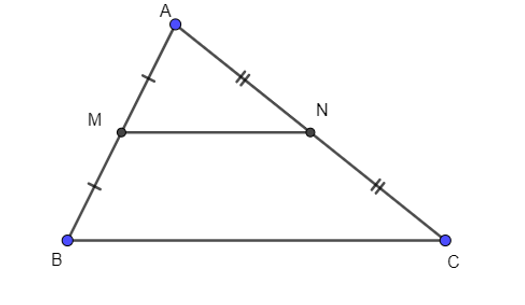
Độ dài đoạn thẳng MN là: