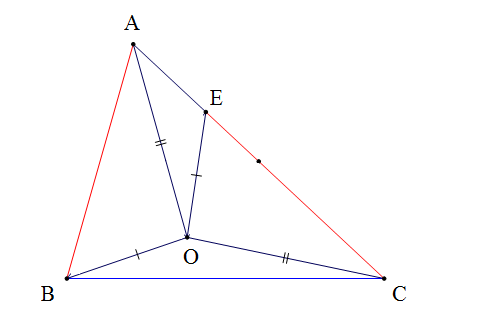
Cho ∆ABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Gọi O là một điểm sao cho OA = OC và OB = OE (hình vẽ). So sánh góc OAB và góc OCA đúng là
A. ;
B. ;
C. ;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Xét ∆AOB và ∆COE có:
AB = CE (giả thiết)
OA = OC (giả thiết)
OB = OE (giả thiết)
Suy ra ∆AOB = ∆COE (c.c.c)
Do đó (hai góc tương ứng) hay .
Cho tam giác MNP có và . Trong các khẳng định dưới đây, khẳng định bào đúng?
Cho ∆ABC có diện tích là 180 cm2 và cạnh BC = 20 cm. Độ dài đường cao ứng với cạnh BC là
Cho tam giác MNP có MN = MP và góc P có số đo là 60°. Khẳng định nào dưới đây sai?
Cho tam giác ABC và tam giác DEF có AB = DE, AC = DF, . Biết . Số đo góc E là
Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở K. Từ B kẻ đường thẳng vuông góc với AK tại H và cắt AC ở D. Chọn câu sai.
Cho tam giác ABC có AD là khoảng cách từ A đến BC và BE là khoảng cách từ E đến AC. So sánh nào dưới đây đúng?
Cho tam giác KIL có góc I là 62°. Đường phân giác góc K và góc L cắt nhau tại O. Số đo góc KIO là