Cho phương trình với m là tham số. Có bao nhiêu giá trị nguyên của để phương trình đã cho có nghiệm?
A. 20
B. 19
C. 9
D. 21
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B.
Điều kiện
Ta có .
Xét hàm số , , do đó từ (1) suy ra .
Xét hàm số , , .
Bảng biến thiên
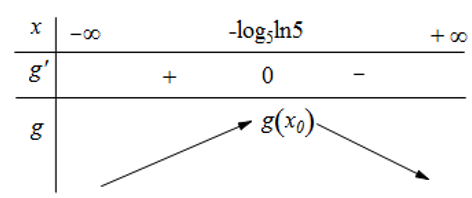
Do đó để phương trình có nghiệm thì .
Các giá trị nguyên của là , có 19 giá trị m thỏa mãn.
Với a,b là các số thực dương tùy ý thỏa mãn , mệnh đề nào dưới đây đúng?
Cho phương trình (m là tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn .
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử?
Cho phương trình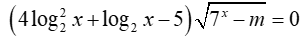 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt
( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt
Có bao nhiêu cặp số nguyên dương sao cho và ứng với mỗi cặp tồn tại đúng 3 số thực thỏa mãn ?