A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
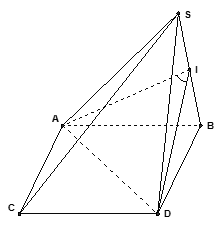
Gọi độ dài cạnh của hình chóp đều S.ABCD là a . Gọi I là trung điểm của SB ta có (vì tam giác SBD đều) và (vì tam giác SAB đều). Vậy, góc giữa hai mặt phẳng (SAB) và (SAD) chính là góc .
Ta có : (đường chéo hình vuông), (đường cao tam giác đều)
Áp dụng định lý cosin cho góc I trong tam giác AID ta có :
Vậy
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm O và . Khẳng định nào sau đây sai ?
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc . Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và . Gọi E là trung điểm BC và F là trung điểm BE . Góc giữa hai mặt phẳng (SOF) và (SBC) là
Cho hình lập phương . Gọi là góc giữa hai mặt phẳng (A1D1CB) và (ABCD). Chọn khẳng định đúng trong các khẳng định sau?