Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD. Chứng minh ba điểm B, C, E thẳng hàng.
 Giải bởi Vietjack
Giải bởi Vietjack

Xét ∆OEC và ∆ODC có:
OE = OD (giả thiết)
\(\widehat {EOC} = \widehat {DOC}\) (vì Ot là tia phân giác của \(\widehat {xOy}\)).
Cạnh OC chung
Do đó ∆OEC = ∆ODC (c.g.c)
Suy ra \(\widehat {ECO} = \widehat {OCD}\) (hai góc tương ứng)
Ta có \[\widehat {OCD} = \widehat {ACH}\] (đối đỉnh) hay \(\widehat {ECO} = \widehat {OCD} = \widehat {ACH} = \widehat {HCB}\)
Vì ba điểm A, C, D thẳng hàng nên \(\widehat {ACH} + \widehat {HCB} + \widehat {MCD} = 180^\circ \)
hay \(\widehat {ECO} + \widehat {OCD} + \widehat {BCD} = 180^\circ \) hay ba điểm E, C, B thẳng hàng.
Ba đơn vị cùng vận chuyển 700 tấn hàng. Đơn vị A có 10 xe trọng tải mỗi xe là 5 tấn; đơn vị B có 20 xe trọng tải mỗi xe là 4 tấn; đơn vị C có 14 xe trọng tải mỗi xe là 5 tấn. Hỏi mỗi đơn vị vận chuyển được bao nhiêu tấn hàng, biết mỗi xe đều chở một số chuyến như nhau?
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Chứng minh rằng \(\frac{{ab}}{{cd}} = \frac{{{a^2} - {b^2}}}{{{c^2} - {d^2}}}\).
Tỉ lệ thức nào sau đây không được lập từ tỉ lệ thức \(\frac{{14}}{8} = \frac{{21}}{{12}}\)?
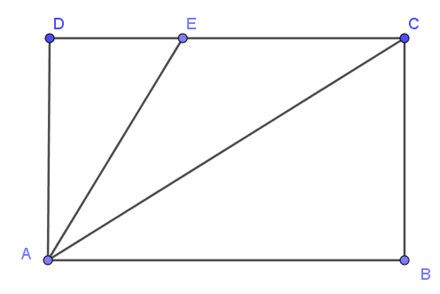
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:
|
x |
−5 |
1 |
|
y |
1 |
? |
Giá trị cần điền vào “?” là
Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi x = –2 thì y = 4. Khi đó, hệ số a bằng bao nhiêu?
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
Chứng minh OA = OB.
\(\frac{{ - 6}}{x} = \frac{9}{{ - 15}}\);
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
Lấy điểm C nằm giữa O và H. Chứng minh \(\widehat {ACH} = \widehat {HCB}\).
\(\frac{{3x - 7}}{8} = \frac{5}{2}\)
\(\frac{{ - 4}}{x} = \frac{x}{{ - 49}}\)
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.