Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, , . Góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng 60o . Bán kính mặt cầu ngoại tiếp tứ diện A'.ABC bằng:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
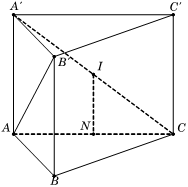
Ta có
Trong , ta có
Trong , ta có
Gọi N là trung điểm AC, suy ra N là tâm đường tròn ngoại tiếp
Gọi I là trung điểm A'C , suy ra
Do đó IN là trục của , suy ra
Hơn nữa, tam giác A'AC vuông tại A có I là trung điểm A'C nên IA' = IC = IA (2)
Từ (1) và (2), ta có IA' = IA = IB = IC hay I là tâm của mặt cầu ngoại tiếp hình chóp A'.ABC với bán kính .Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
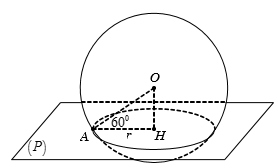
Cho mặt cầu S(O;R), A là một điểm ở trên mặt cầu (S) và (P) là mặt phẳng qua A sao cho góc giữa OA và (P) bằng 60o . Diện tích của đường tròn giao tuyến bằng:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, BD = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng 60o . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD nhận giá trị nào sau đây?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc . Cạnh bên và vuông góc với đáy (ABCD). Bán kính mặt cầu ngoại tiếp khối chóp S.ACD nhận giá trị:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = AC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi I là trung điểm của BC, SI tạo với đáy (ABC) một góc 60o . Gọi S, V lần lượt là diện tích mặt cầu và thể tích khối cầu ngoại tiếp hình chóp S.ABC. Tỉ số bằng ?
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc 60o và điểm G là trọng tâm tam giác ABC. Bán kính mặt cầu ngoại tiếp khối chóp G.A'B'C' bằng:
Trong không gian Oxyz cho đường tròn . Bán kính r của đường tròn (C) bằng :