Bất phương trình có tập nghiệm là . Tổng có giá trị bằng
A. -2
B. 4
C. 5
D. 3
 Giải bởi Vietjack
Giải bởi Vietjack
Điều kiện:
Xét trên đoạn .
Có , do đó hàm số đồng biến trên .
Bất phương trình đã cho
So với điều kiện, tập nghiệm của bất phương trình là .
Chọn C.
Các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng là
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn để hàm số đồng biến trên R?
Có bao nhiêu giá trị nguyên không âm của tham số m sao cho hàm số nghịch biến trên đoạn ?
Cho hàm số có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng dưới đây nào
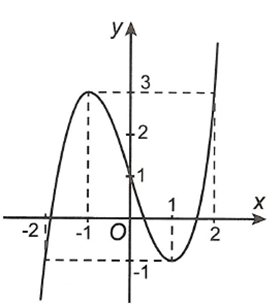
Có tất cả bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng ?
Cho hàm số có bảng xét dấu của đạo hàm như sau

Hàm số nghịch biến trên khoảng nào sau đây?
Có bao nhiêu giá trị nguyên m để hàm số nghịch biến trên khoảng .
Tìm các giá trị nguyên âm của tham số m để hàm số nghịch biến trên đoạn .
Cho hàm số xác định trên khoảng có tính chất
và, .
Tìm khẳng định đúng trong các khẳng định sau.
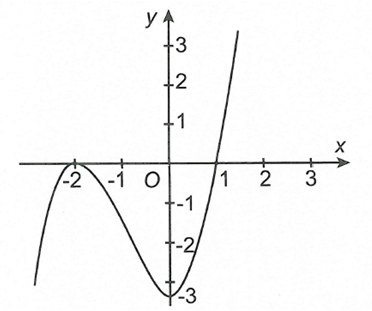
Tìm các giá trị m để hàm số đồng biến trên đoạn có độ dài bằng 2.
Gọi S là tập hợp các giá trị của tham số m để hàm số
đồng biến trên R .
Tổng giá trị của tất cả các phần tử thuộc S bằng
Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng ?