A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Tập xác định: . Ta có .
Hàm số có hai điểm cực trị khi và chỉ khi có hai nghiệm phân biệt .
Đường cong qua hai điểm cực trị có phương trình là .
Ta viết phương trình đường cong dưới dạng .
Ta chọn k sao cho nghiệm của mẫu là nghiệm của tử để có thể rút gọn thành hàm số bậc nhất. Vì là nghiệm của mẫu, nên thế vào tử ta được .
Với : .
Điểm (thỏa mãn) .
Chọn B.
Số giá trị nguyên của tham số để hàm số
có hai điểm cực trị trái dấu là
Cho hàm số có đạo hàm cấp hai liên tục trên R. Trên hình vẽ là đồ thị hàm số trên đoạn (và hàm số nghịch biến trên ), đồ thị của hàm số trên đồ thị của hàm số trên (và hàm số luôn đồng biến trên ). Hàm số có tối đa bao nhiêu điểm cực trị?
![Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên R. Trên hình vẽ là đồ thị hàm số y=f(x) trên đoạn ( - vô cùng, a] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid17-1672847180.png)
Cho hàm số liên tục trên R, có đạo hàm với là hàm đa thức có đồ thị như hình vẽ dưới đây (đồng biến trên và trên . Số điểm cực trị của hàm số là
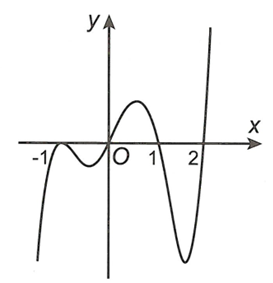
Hàm số đạt cực tiểu tại điểm và đạt cực đại tại điểm . Giá trị của biểu thức là
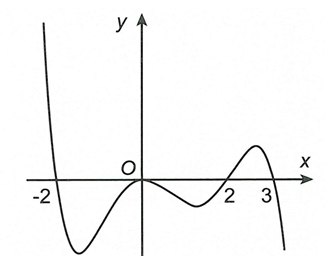
Cho hàm số có đạo hàm đến cấp 2 trên R và có đồ thị hàm số như hình vẽ dưới đây (đồ thị chỉ có 4 điểm chung với trục hoành như hình vẽ). Số điểm cực trị tối đa của hàm số là
Cho hàm số liên tục trên đoạn và có đồ thị trên đoạn như hình vẽ bên. Đồ thị hàm số có bao nhiêu điểm cực đại?
![Cho hàm số y=f(x) liên tục trên đoạn [-4,3] và có đồ thị trên đoạn [-4,3] như hình vẽ bên. Đồ thị hàm số có bao nhiêu điểm cực đại? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid15-1672846519.png)
Cho hàm số y= f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ dưới đây

Số điểm cực trị của hàm số y=f(x) là
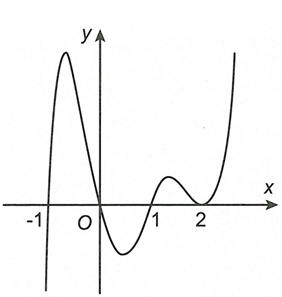
Cho hàm số y=f(x) liên tục trên R, có đạo hàm với có đồ thị như hình vẽ dưới đây ( đồng biến trên và trên ). Hàm số có bao nhiêu điểm cực trị?
Cho hàm số y=f(x) có bảng biến thiên của f'(x) như hình vẽ dưới đây
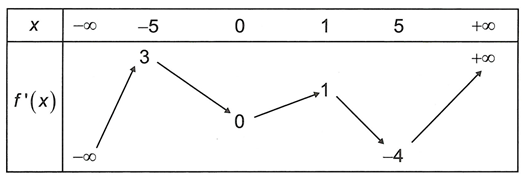
Số điểm cực trị của hàm số y=f(x) là
Cho hàm số liên tục trên và có bảng xét dấu đạo hàm như hình vẽ dưới đây

Số điểm cực trị của hàm số là