A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Ta có
Từ (1) suy ra thay vào (2) ta được (2) (3)
Xét hàm số có tập xác định
Bảng biến thiên
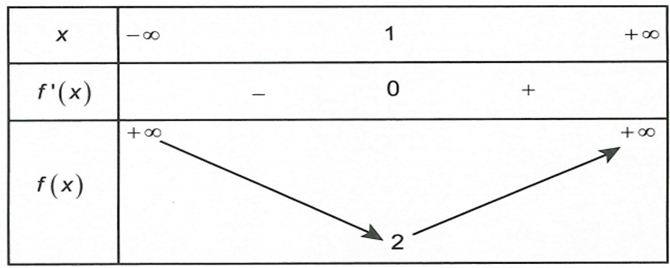
Hệ đã cho có nghiệm thực khi và chỉ khi phương trình (3) có nghiệm thực
Dựa vào bảng biến thiên ta được . Chọn D
Một người thợ xây, muốn xây một bồn chứa thóc hình trụ tròn với thể tích là (như hình vẽ). Đáy làm bằng bê tông, thành làm bằng tôn và nắp bể làm bằng nhôm. Biết giá thành các vật liệu như sau: bê tông 100 nghìn đồng một , tôn 90 nghìn một và nhôm 120 nghìn đồng một . Chi phí thấp nhất để làm bồn chứa thóc (làm tròn đến hàng nghìn) là
Một chất điểm chuyển động có phương trình chuyển động là , với t (s) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (m) là quãng đường vật đi được trong khoảng thời gian đó. Trong khoảng thời gian 6 giây đầu tiên, vận tốc v (m/s) của chất điểm đạt giá trị lớn nhất bằng
Cho hàm số có bảng biến thiên như hình vẽ
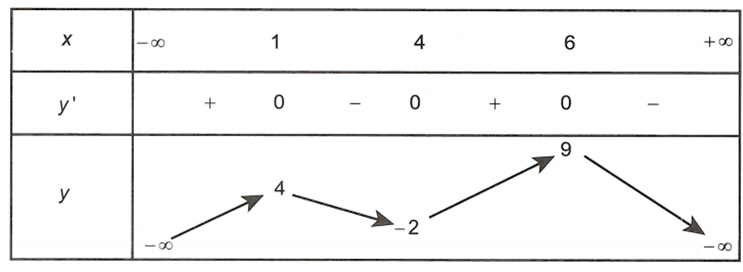
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn lần lượt là M, m. Tổng bằng
Thầy Toản có thanh gỗ dài là 3,2 m. Thầy Toản dự định dùng thanh gỗ để thiết kế 5 hình tam giác giống nhau làm kệ trang trí phòng đọc sách, trong đó các tam giác có 1 cạnh có độ dài là 24 cm (coi các mẩu cắt bỏ đi không đáng kể). Tổng diện tích của 5 tam giác có giá trị lớn nhất là

Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường s (mét) đi được của đoàn tàu là một hàm số của thời gian t (giây), hàm số đó là . Thời điểm t (giây) mà tại đó vận tốc v(m/s) của chuyển động đạt giá trị lớn nhất là
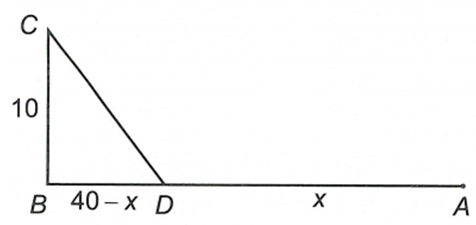
Một người cần đi từ khách sạn A bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 40km. Người đó có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy (như hình vẽ bên). Biết kinh phí đi đường thủy là 5 USD/km, đi đường bộ là 3 USD/km. Hỏi người đó phải đi đường bộ một khoảng bao nhiêu để kinh phí nhỏ nhất?
Cho hàm số liên tục trên R và có đồ thị như hình vẽ dưới đây. Khi đó giá trị lớn nhất của hàm số trên nửa khoảng là
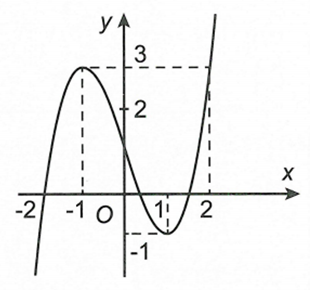
Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ bên dưới.
![Cho hàm số y=f(x) liên tục trên đoạn [-1,3] và có đồ thị như hình vẽ bên dưới. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/01/blobid5-1673793734.png)
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn . Giá trị của bằng
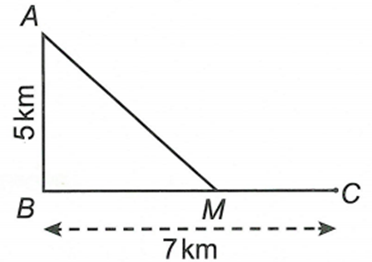
Một ngọn hải đăng đặt ở vị trí A cách bờ biển một khoảng AB = 5 (km). Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7(km). Người canh hải đăng có thể chèo đò từ A đến vị trí M trên bờ biển với vận tốc 4 (km/h) rồi đi bộ từ M đến C với vận tốc 6 (km/h). Vị trí của điểm M cách B một khoảng gần nhất với giá trị nào sau đây để người đó đến kho nhanh nhất?
Cho x, y là các số thực thỏa mãn . Giá trị nhỏ nhất của biểu thức bằng
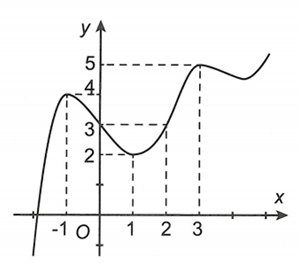
Cho hàm số liên tục trên R và có đồ thị như hình vẽ bên. Gọi M, m theo thứ tự là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn . Tổng bằng
Cho hệ phương trình . Có bao nhiêu giá trị nguyên của tham số để hệ phương trình có nghiệm?
Cho hàm số liên tục trên và có đồ thị như hình vẽ
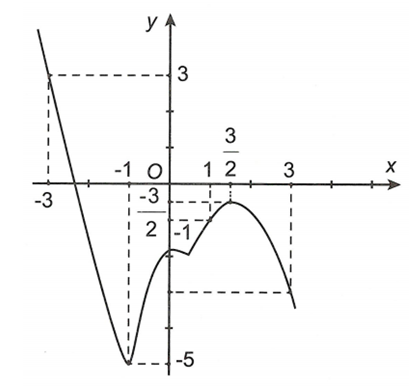
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn . Tổng bằng
Gọi S là tập tất cả các giá trị nguyên âm của tham số m để phương trình có nghiệm. Tập S có số phần tử là