Giải bởi Vietjack
Giải bởi Vietjack
Một vật chuyển động theo quy luật \(S = - \frac{1}{2}{t^3} + 9{t^2},\) với \(t\)(giây) là khoảng thời gian tính từ
Cho hàm số \(f(x)\), có bảng biến thiên của hàm số \(f'(x)\) như sau:

Số cực trị của hàm số \(y = f({x^2} + 2x)\) là
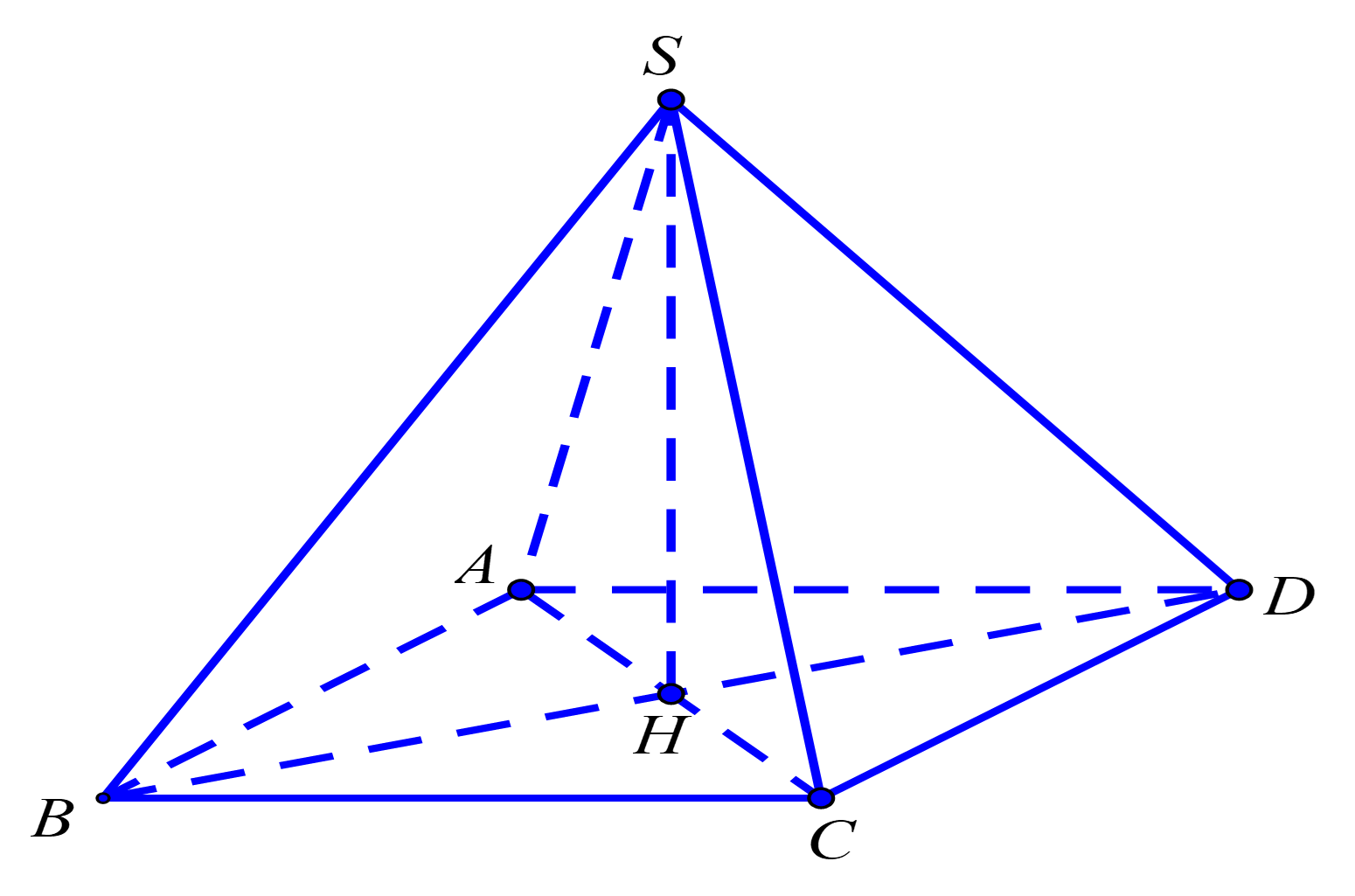
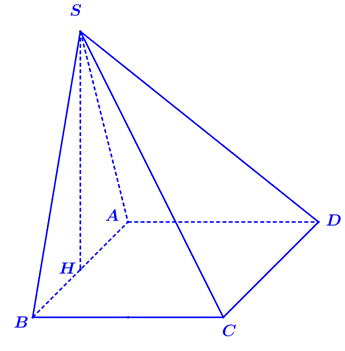
Cho \(S.ABCD\)là hình chóp tứ giác đều, biết \[AB = a,\,\,SA = a\]. Thể tích của khối chóp \(S.ABCD\) bằng