Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án (Đề 1)
-
4208 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
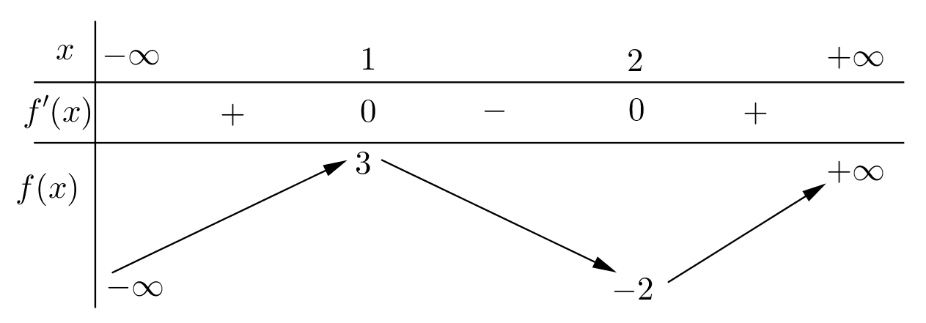
Câu 1:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
 Xem đáp án
Xem đáp án
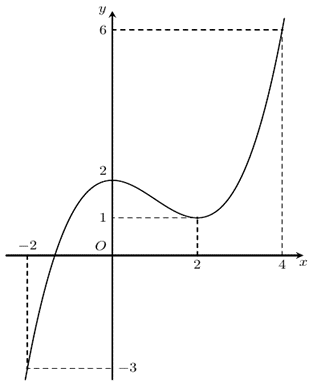
Câu 2:
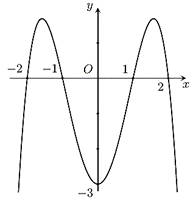
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số như hình vẽ sau:
 Xem đáp án
Xem đáp án
Câu 3:
 Xem đáp án
Xem đáp án
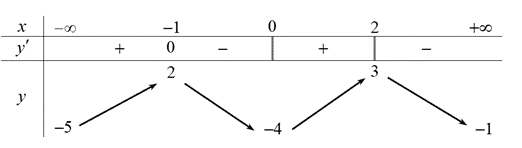
Câu 4:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
 Xem đáp án
Xem đáp án
Câu 5:
 Xem đáp án
Xem đáp án
Câu 6:
 Xem đáp án
Xem đáp án
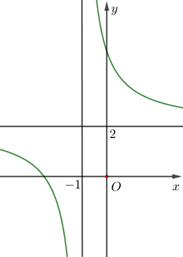
Câu 7:
 Xem đáp án
Xem đáp án
Câu 8:
 Xem đáp án
Xem đáp án
Câu 9:
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau:
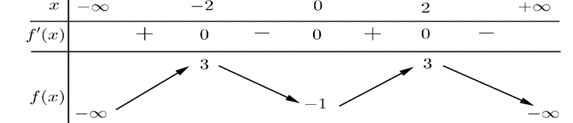
 Xem đáp án
Xem đáp án
Câu 10:
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\)có đồ thị như hình vẽ sau.
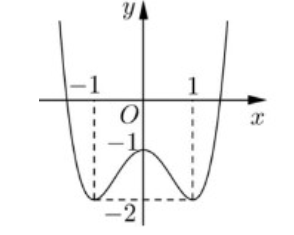
 Xem đáp án
Xem đáp án
Câu 11:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
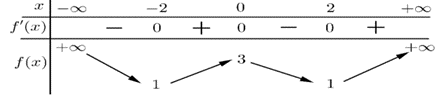
 Xem đáp án
Xem đáp án
Câu 12:
 Xem đáp án
Xem đáp án
Câu 13:
 Xem đáp án
Xem đáp án
Câu 14:
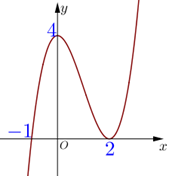
 Xem đáp án
Xem đáp án
Câu 15:
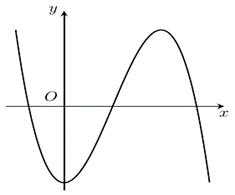
 Xem đáp án
Xem đáp án
Câu 16:
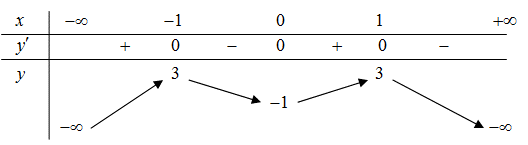
 Xem đáp án
Xem đáp án
Câu 17:
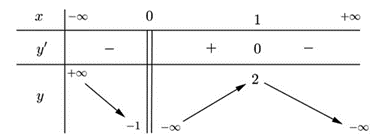
 Xem đáp án
Xem đáp án
Câu 18:
 Xem đáp án
Xem đáp án
Câu 19:
 Xem đáp án
Xem đáp án
Câu 20:
 Xem đáp án
Xem đáp án
Câu 21:
 Xem đáp án
Xem đáp án
Câu 22:
Cho \(S.ABCD\)là hình chóp tứ giác đều, biết \[AB = a,\,\,SA = a\]. Thể tích của khối chóp \(S.ABCD\) bằng
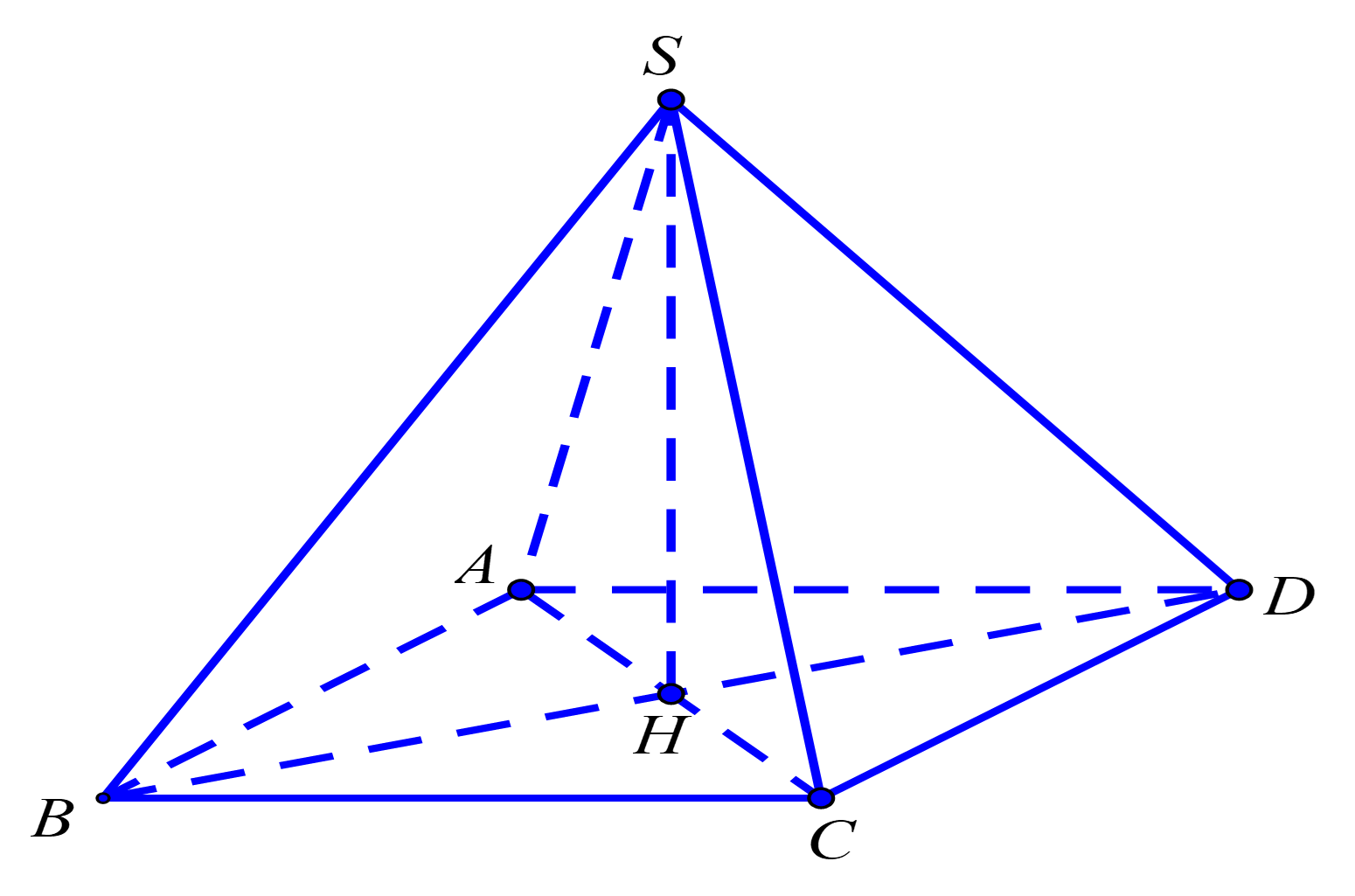
 Xem đáp án
Xem đáp án
Câu 23:
 Xem đáp án
Xem đáp án
Câu 24:
 Xem đáp án
Xem đáp án
Câu 25:
 Xem đáp án
Xem đáp án
Câu 26:
 Xem đáp án
Xem đáp án
Câu 27:
 Xem đáp án
Xem đáp án
Câu 28:
 Xem đáp án
Xem đáp án
Câu 29:
 Xem đáp án
Xem đáp án

Câu 30:
 Xem đáp án
Xem đáp án
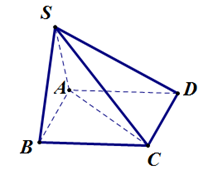
Câu 31:
 Xem đáp án
Xem đáp án
Câu 32:
 Xem đáp án
Xem đáp án
Câu 33:
 Xem đáp án
Xem đáp án
Câu 34:
 Xem đáp án
Xem đáp án
Câu 35:
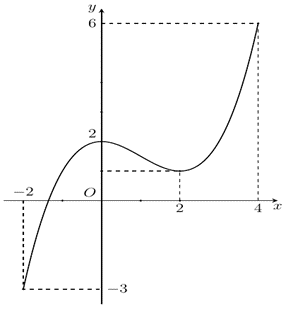
 Xem đáp án
Xem đáp án
Chọn A
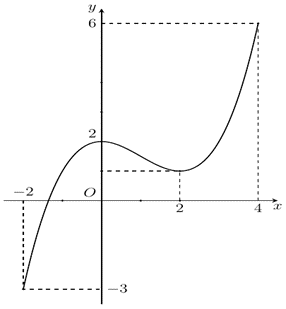
Câu 36:
Một vật chuyển động theo quy luật \(S = - \frac{1}{2}{t^3} + 9{t^2},\) với \(t\)(giây) là khoảng thời gian tính từ
 Xem đáp án
Xem đáp án
Lời giải
Câu 37:
 Xem đáp án
Xem đáp án
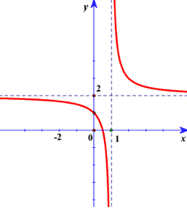
Câu 38:
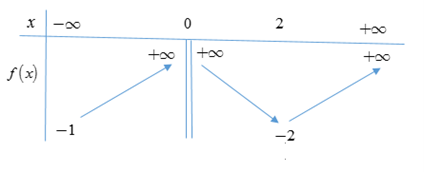
Cho hàm số \(y = f\left( x \right)\)có đạo hàm trên \(\mathbb{R}\)và có đồ thị như hình vẽ sau:
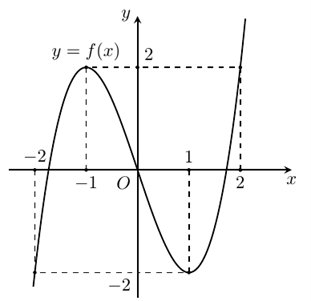
 Xem đáp án
Xem đáp án
Câu 39:
 Xem đáp án
Xem đáp án
Câu 40:
 Xem đáp án
Xem đáp án
Câu 41:
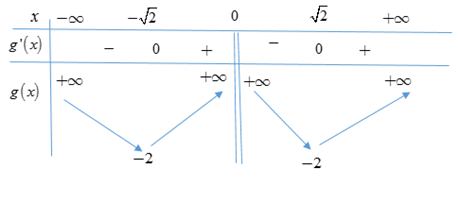
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\)và có bảng biến thiên như
 Xem đáp án
Xem đáp án
Câu 42:
 Xem đáp án
Xem đáp án
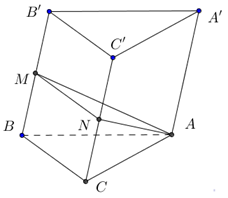
Câu 43:
 Xem đáp án
Xem đáp án
Câu 44:
 Xem đáp án
Xem đáp án
Câu 45:
 Xem đáp án
Xem đáp án
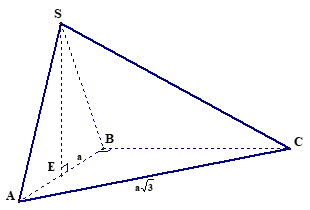
Câu 46:
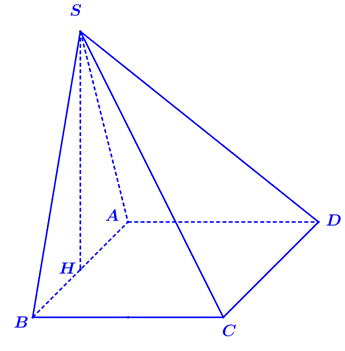
 Xem đáp án
Xem đáp án
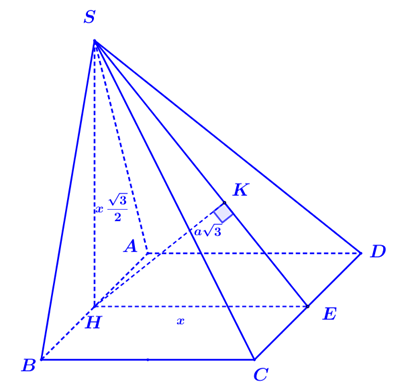
Câu 47:
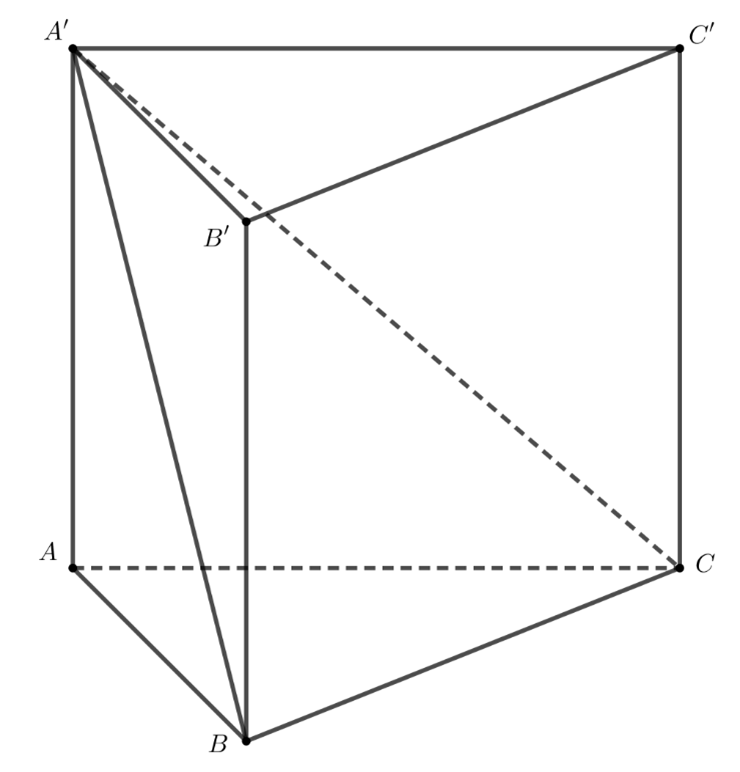
 Xem đáp án
Xem đáp án
Câu 48:
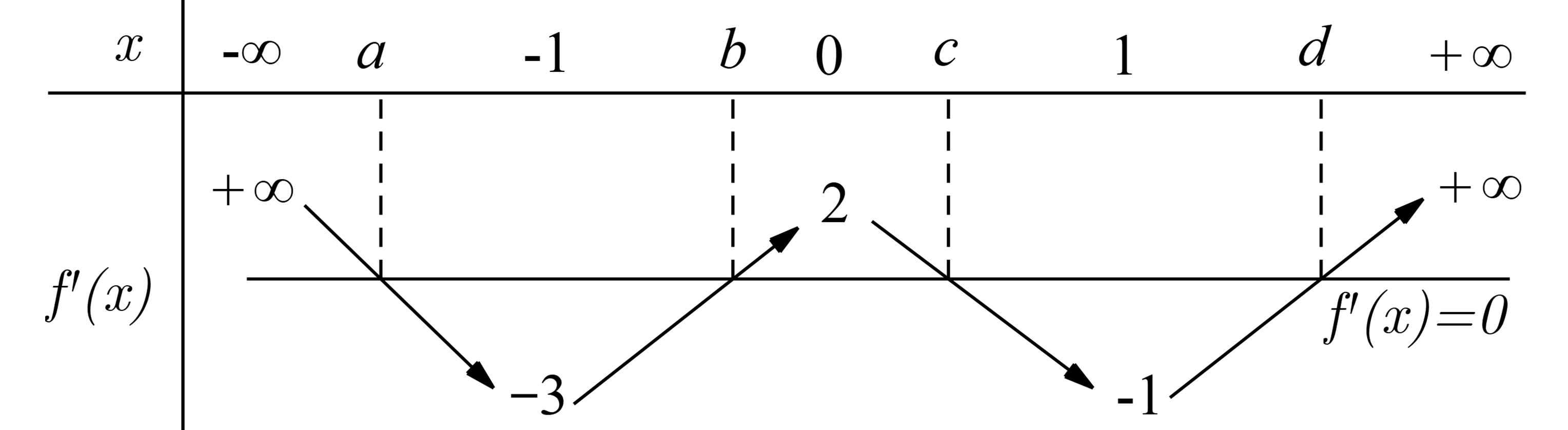
Cho hàm số \(f(x)\), có bảng biến thiên của hàm số \(f'(x)\) như sau:

Số cực trị của hàm số \(y = f({x^2} + 2x)\) là
 Xem đáp án
Xem đáp án

Câu 49:
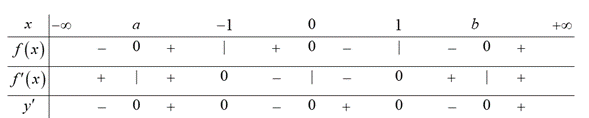
Cho hàm số \(y = f\left( x \right)\), có bảng xét dấu \(f'\left( x \right)\) như sau:
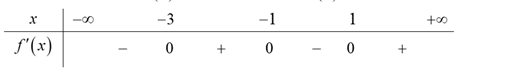
Hàm số \(y = f\left( {3 - 2x} \right)\) đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án

Câu 50:
 Xem đáp án
Xem đáp án
