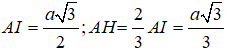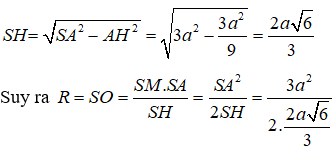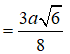Đề kiểm tra 15 phút Toán 12 Chương 2 Hình học có đáp án (Đề 1)
-
3123 lượt thi
-
10 câu hỏi
-
15 phút
Danh sách câu hỏi
Câu 1:
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
Xem đáp án
Chọn A.
Ta có công thức tính diện tích mặt cầu và thể tích hình cầu là:
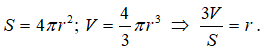
Câu 2:
Cho mặt cầu S(O; R) và điểm A cố định với OA = d. Qua A, kẻ đường thẳng tiếp xúc với mặt cầu S(O; R) tại M. Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM?
Xem đáp án
Chọn B.
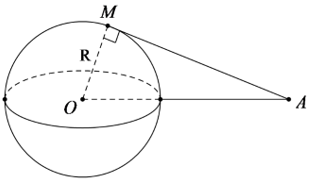
Vì ∆ tiếp xúc với S(O;R) tại M nên OM⊥Δ tại M.
Xét tam giác OMA vuông tại M, ta có:
Câu 3:
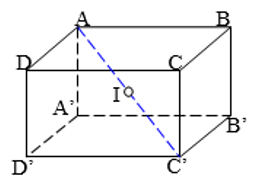
Một hình hộp chữ nhật có ba kích thước là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Tâm của mặt cầu (S) là
Xem đáp án
Chọn D.
Tâm của hình hộp chữ nhật cách đều 8 đỉnh của hình hộp nên tâm của mặt cầu (S) chính là tâm của hình hộp chữ nhật.
Câu 4:
Cho mặt cầu S(O;R) và đường thẳng Δ. Biết khoảng cách từ O tới Δ bằng d. Đường thẳng Δ tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ?
Xem đáp án
Chọn A.
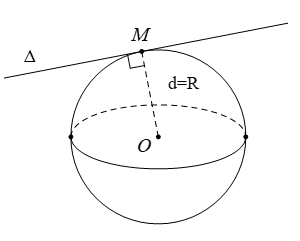
Đường thẳng Δ tiếp xúc với S(O; R) khi d = R.
Câu 5:
Cho hai điểm A, B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
Xem đáp án
Chọn A.
Gọi I là tâm mặt cầu đi qua hai điểm A, B cố định và phân biệt thì ta luôn có IA = IB.
Do đó, I thuộc mặt phẳng trung trực của đoạn AB.
Câu 6:
Cho mặt cầu S(O;R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O;R) là đường tròn có bán kính bằng bao nhiêu?
Xem đáp án
Chọn C.
*) Gọi I là hình chiếu của O lên (α) và M là điểm thuộc đường giao tuyến của (α) và mặt cầu S(O; R).
*) Xét tam giác OIM vuông tại I, ta có: OM = R và OI = d nên 
Câu 7:
Thể tích của một khối cầu là thì bán kính nó là bao nhiêu ?
Xem đáp án
Chọn D.
Thể tích khối cầu bán kính R là:
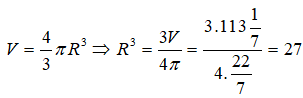
Câu 8:
Một mặt cầu có đường kính 11m thì diện tích của mặt cầu là bao nhiêu? và làm tròn kết quả đến chữ số thập phân thứ hai).
Xem đáp án
Chọn C
Diện tích của mặt cầu là
Câu 9:
Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH, ta được một mặt cầu. Thể tích của khối cầu tương ứng là:
Xem đáp án
Chọn C
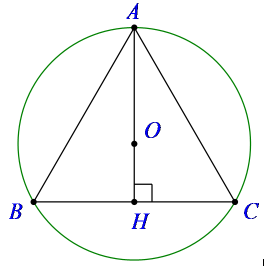
AH là đường cao trong tam giác đều cạnh a nên
Gọi O là tâm mặt cầu ngoại tiếp ΔABC, thì O ∈ AH và
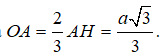
Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là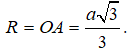 
.
Vậy thể tích của khối cầu tương ứng là:
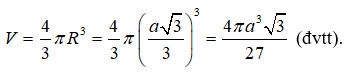
Câu 10:
Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S.ABC, biết các cạnh đáy có độ dài bằng a, cạnh bên .
Xem đáp án
Chọn D.
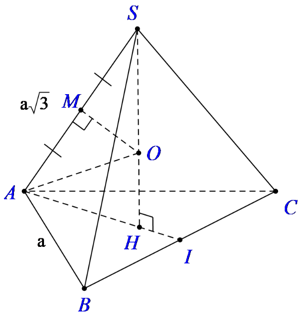
Gọi H là tâm của tam giác đều ABC, ta có SH⊥(ABC) nên SH là trục của tam giác ABC.
Gọi M là trung điểm của SA, trong mp (SAH) kẻ trung trực của SA cắt SH tại O thì OS = OA = OB = OC
Suy ra: O chính là tâm mặt cầu ngoại tiếp hình chóp S.ABC. Bán kính mặt cầu là R = SO.
Vì hai tam giác SMO và SHA đồng dạng nên ta có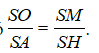 
Ta có:
