Trắc nghiệm Toán 12 Bài 2: Mặt cầu có đáp án (Mới nhất)
-
1290 lượt thi
-
109 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho đường tròn (C) đường kính AB và đường thẳng . Để hình tròn xoay sinh bởi (C) khi quay quanh là một mặt cầu thì cần có thêm điều kiện nào sau đây:
(I) Đường kính AB thuộc .
(II) cố định và đường kính AB thuộc .
(III) cố định và hai điểm A, B cố định trên .
 Xem đáp án
Xem đáp án
Chọn C
Câu 2:
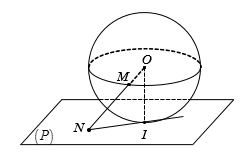
 Xem đáp án
Xem đáp án
Chọn D
Vì I là hình chiếu của O trên (P) nên d[O, (P)] = OI mà d[O, (P)] = R nên I là tiếp điểm của (P) và (S).
Đường thẳng OM cắt (P) tại N nên IN vuông góc với OI tại I. Suy ra IN tiếp xúc với (S).
Tam giác OIN vuông tại I nên
Câu 3:
Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
 Xem đáp án
Xem đáp án
Chọn D
Vì AB tiếp xúc với (S) tại B nên
Suy ra
Câu 4:
 Xem đáp án
Xem đáp án
Chọn B
Gọi H là hình chiếu của O lên BC.
Ta có OB = OC = R, suy ra H là trung điểm của BC nên .
Suy raCâu 5:
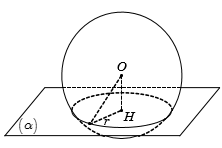
 Xem đáp án
Xem đáp án
Chọn B
Gọi H là hình chiếu của xuống
Ta có nên cắt S(O;R) theo đường tròn C(H;r).
Bán kính đường tròn là
Suy ra đường kính bằngCâu 6:
 Xem đáp án
Xem đáp án
Chọn C
Mặt phẳng cắt mặt cầu S(I;2,6cm) theo một đường tròn (H,r).
VậyCâu 7:
 Xem đáp án
Xem đáp án
Chọn D
Hình tròn lớn của hình cầu S là hình tròn tạo bởi mặt phẳng cắt hình cầu và đi qua tâm của hình cầu. Gọi R là bán kính hình cầu thì hình tròn lớn cũng có bán kính là R .
Theo giả thiết, ta có và
Suy raCâu 8:
 Xem đáp án
Xem đáp án
Chọn A
Gọi khoảng cách từ tâm cầu đến mặt phẳng là d , ta có
Theo giả thiết và
VậyCâu 9:
Cho mặt cầu S(O;R), A là một điểm ở trên mặt cầu (S) và (P) là mặt phẳng qua A sao cho góc giữa OA và (P) bằng 60o . Diện tích của đường tròn giao tuyến bằng:
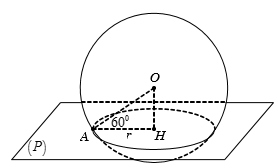
 Xem đáp án
Xem đáp án
Chọn C
Gọi H là hình chiếu vuông góc của O trên (P) thì
● H là tâm của đường tròn giao tuyến của (P) và (S)
●
Bán kính của đường tròn giao tuyến:
Suy ra diện tích đường tròn giao tuyến:Câu 10:
 Xem đáp án
Xem đáp án
Chọn B
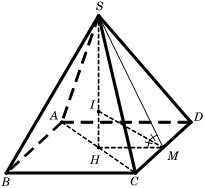
Gọi H là tâm của hình vuông ABCD.
Ta có SH là trục đường tròn ngoại tiếp đáy.
Gọi M là trung điểm của CD và I là chân đường phân giác trong của góc
Suy ra I là tâm của mặt cầu nội tiếp hình chóp, bán kính r = IH
Ta có:
Dựa vào tính chất của đường phân giác ta có:
Câu 11:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và BA = BC = a. Cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
 Xem đáp án
Xem đáp án
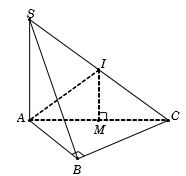
Gọi M là trung điểm AC, suy ra M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi I là trung điểm SC, suy ra IM // SA nên
Do đó IM là trục của , suy ra IA = IB = IC
Hơn nữa, tam giác SAC vuông tại A có I là trung điểm SC nên IS = IC = IA
Từ (1) và (2) ta có IS = IA = IB = IC hay I là tâm của mặt cầu ngoại tiếp hình chóp S.ABC.
Vậy bán kínhCâu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên và vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD ta được:
 Xem đáp án
Xem đáp án
Chọn B
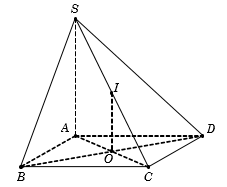
Gọi , suy ra O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Gọi I là trung điểm SC, suy ra
Do đó IO là trục của hình vuông ABCD, suy ra IA = IB = IC = ID (1)
Tam giác SAC vuông tại A có I là trung điểm cạnh huyền SC nên IS = IC = IA. (2)
Từ (1) và (2), ta có:
Vậy diện tích mặt cầu (đvdt).Câu 13:
 Xem đáp án
Xem đáp án
Chọn B
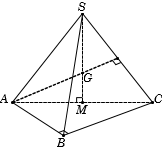
Gọi M là trung điểm AC, suy ra
Tam giác SAC có SM là đường cao và cũng là trung tuyến nên tam giác SAC cân tại S.
Ta có , suy ra tam giác SAC đều.Gọi G là trọng tâm , suy ra (1)
Tam giác ABC vuông tại B, có M là trung điểm cạnh huyền AC nên M là tâm đường tròn ngoại tiếp tam giác ABC.
Lại có nên SM là trục của tam giác ABC.
Mà G thuộc SM nên suy ra (2)
Từ (1) và (2) , suy ra hay G là tâm mặt cầu ngoại tiếp khối chóp S.ABC .
Bán kính mặt cầuCâu 14:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng . Gọi h là chiều cao của khối chóp và R là bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số bằng:
 Xem đáp án
Xem đáp án
Chọn C
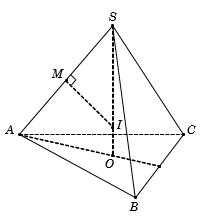
Gọi O là tâm , suy ra và
Trong SOA, ta có
Trong mặt phẳng SOA, kẻ trung trực d của đoạn SA cắt SO tại I, suy ra
● nên IS = IA
● nên IA = IB = IC
Do đó IA = IB IC = IS nên I là tâm mặt cầu ngoại tiếp khối chóp S.ABC
Gọi M là tung điểm SA, ta có nên
VậyCâu 15:
 Xem đáp án
Xem đáp án
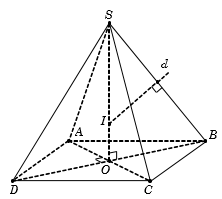
Gọi , suy ra
Ta có
Trong , ta có
Ta có SO là trục của hình vuông ABCD.
Trong mặt phẳng SOB, kẻ đường trung trực d của đoạn SB
Gọi
Xét có đều.
Do đó d cũng là đường trung tuyến của . Suy ra I là trọng tâm .
Bán kính mặt cầu . Suy raCâu 16:
 Xem đáp án
Xem đáp án
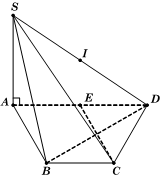
Ta có hay
Gọi E là trung điểm AD
Ta có EA = AB = BC nên ABCE là hình thoi.
Suy ra
Do đó tam giác ACD vuông tại C. Ta có:
hay
Tương tự, ta cũng có hay
Ta có nên khối chóp S.ABCD nhận trung điểm I của SD làm tâm mặt cầu ngoại tiếp, bán kính . Suy raCâu 17:
 Xem đáp án
Xem đáp án
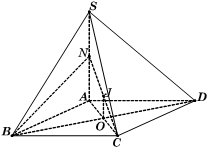
Ta có
Trong , ta có
Ta có
Lại có . Do đó hai điểm A, B cùng nhìn đoạn NC dưới một góc vuông nên hình chóp N.ABC nội tiếp mặt cầu tâm J là trung điểm NC, bán kính
Câu 18:
 Xem đáp án
Xem đáp án
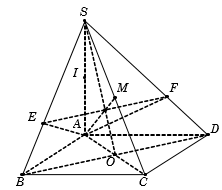
Mặt phẳng song song với BD cắt SB, SD lần lượt tại E, F nên EF // BD
cân tại A, trung tuyến AM nên
Ta có
Do đó (2)
Từ (1) và (2), suy ra (*)
Lại có (**)
Từ (*) và (**), suy ra . Tương tự ta cũng có
Do đó nên năm điểm S, A, E, M, F cùng thuộc mặt cầu tâm I là trung điểm của SA, bán kính .Câu 19:
 Xem đáp án
Xem đáp án
Chọn C
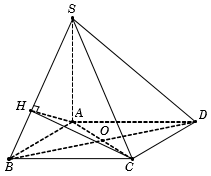
Gọi
Vì ABCD là hình vuông nên OB = OD = OC (1)
Ta có
Lại có
Suy ra nên tam giác AHC vuông tại H và có O là trung điểm cạnh huyền AC nên suy ra OH = OC. (2)
Từ (1) và (2), suy ra
Câu 20:
 Xem đáp án
Xem đáp án
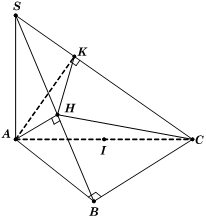
Theo giả thiết, ta có và (1)
Do (2)
Từ (1) và (2), suy ra ba điểm B, H, K cùng nhìn xuống AC dưới một góc 90o nên hình chóp A.HKCB nội tiếp mặt cầu tâm I là trung điểm AC, bán kính
Vậy thể tích khối cầu (đvtt).Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, BD = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng 60o . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD nhận giá trị nào sau đây?
 Xem đáp án
Xem đáp án
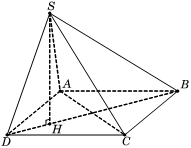
Ta có
Trong tam giác vuông SHB, có
và
Trong tam giác vuông SHB, có
Xét tam giác SBD, ta có
Suy ra tam giác SBD vuông tại S
Vậy các đỉnh S, A, C cùng nhìn xuống BD dưới một góc vuông nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là O, bán kínhCâu 22:
 Xem đáp án
Xem đáp án
Chọn D
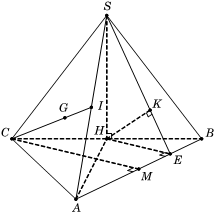
Ta có
Tam giác ABC đều cạnh a nên
Trong tam giác vuông SHA, ta có
Vì mặt cầu có tâm G và tiếp xúc với nên bán kính mặt cầu
Ta có
Gọi M, E lần lượt là trung điểm AB và MB
Suy ra và
Gọi K là hình chiếu vuông góc của H trên SE, suy ra . (1)
Ta có (2)
Từ (1) và (2), suy ra nên
Trong tam giác vuông SHE, ta có
Vậy
Câu 23:
 Xem đáp án
Xem đáp án
Chọn A
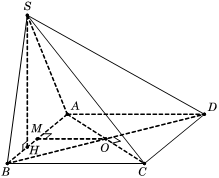
Gọi
Suy ra (1)
Gọi M là trung điểm AB , do tam giác SAB vuông tại S nên MS = MA = MB.
Gọi H là hình chiếu của S trên AB
Từ giả thiết suy r
Ta có nên OM là trục của tam giác SAB, suy ra OA = OB = OS (2)
Từ (1) và (2) , ta có OS = OA = OB = OC = OD
Vậy O là tâm mặt cầu ngoại tiếp khối chóp S.ABCD, bán kính
Suy ra (đvtt).Câu 24:
Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh bằng a. Cạnh bên và vuông góc với đáy (ABC). Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:
 Xem đáp án
Xem đáp án
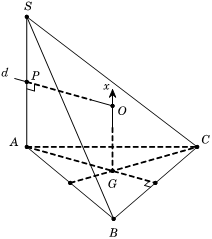
Gọi G là trọng tâm , suy ra G là tâm đường tròn ngoại tiếp
Từ G dựng tia (như hình vẽ).
Suy ra Gx là trục của tam giác ABC
Trong mặt phẳng (SA, Gx) kẻ trung trực d của đoạn thẳng SA
Gọi
Suy ra O là tâm mặt cầu ngoại tiếp khối chóp S.ABC
Ta có
Trong tam giác vuông OGA, ta cóCâu 25:
Cho tứ diện O.ABC có các cạnh OA, OB, OC đôi một vuông góc và OA = a, OB = 2a, OC = 3a. Bán kính mặt cầu ngoại tiếp tứ diện O.ABC là:
 Xem đáp án
Xem đáp án
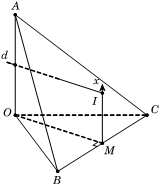
Gọi M là trung điểm BC, suy ra M là tâm đường tròn ngoại tiếp
Kẻ (như hình vẽ).
Suy ra Mx là trục của
Trong mặt phẳng (OA, Mx), kẻ trung trực d của đoạn thẳng OA cắt Mx tại I
Khi đó I chính là tâm mặt cầu ngoại tiếp tứ diện.
Bán kính mặt cầu:Câu 26:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = AC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi I là trung điểm của BC, SI tạo với đáy (ABC) một góc 60o . Gọi S, V lần lượt là diện tích mặt cầu và thể tích khối cầu ngoại tiếp hình chóp S.ABC. Tỉ số bằng ?
 Xem đáp án
Xem đáp án
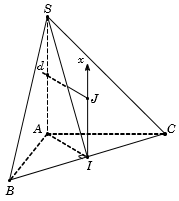
Ta có
Tam giác ABC vuông cân tại A, suy raTrong , ta có
Kẻ (như hình vẽ).
Suy ra Ix là trục của
Trong mặt phẳng (SA,Ix), kẻ trung trực d của đoạn thẳng SA cắt Ix tại J. Khi đó J chính là tâm mặt cầu ngoại tiếp hình chóp.
Bán kính: nênCâu 27:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc . Cạnh bên và vuông góc với đáy (ABCD). Bán kính mặt cầu ngoại tiếp khối chóp S.ACD nhận giá trị:
 Xem đáp án
Xem đáp án
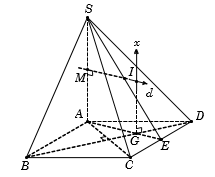
Gọi G là trọng tâm tam giác đều ACD. Kẻ , suy ra Gx là trục của
Khi đó I chính là tâm mặt cầu ngoại tiếp.
Ta có
Suy ra bán kính:
Câu 28:
 Xem đáp án
Xem đáp án
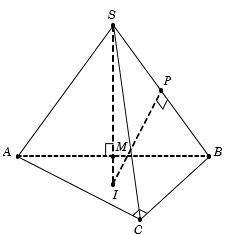
Gọi M là trung điểm AB, suy ra và
Do đó SM là trục của tam giác ABC
Trong mặt phẳng (SMB) , kẻ đường trung trực d của đoạn SB cắt SM tại I. Khi đó I là tâm mặt cầu ngoại tiếp hình chóp S.ABC , bán kính R = RI
Trong tam giác vuông SMB, ta có
Ta có , suy ra
Câu 29:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, , . Góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng 60o . Bán kính mặt cầu ngoại tiếp tứ diện A'.ABC bằng:
 Xem đáp án
Xem đáp án
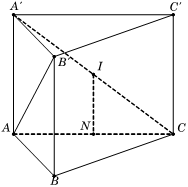
Ta có
Trong , ta có
Trong , ta có
Gọi N là trung điểm AC, suy ra N là tâm đường tròn ngoại tiếp
Gọi I là trung điểm A'C , suy ra
Do đó IN là trục của , suy ra
Hơn nữa, tam giác A'AC vuông tại A có I là trung điểm A'C nên IA' = IC = IA (2)
Từ (1) và (2), ta có IA' = IA = IB = IC hay I là tâm của mặt cầu ngoại tiếp hình chóp A'.ABC với bán kính .Câu 30:
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc 60o và điểm G là trọng tâm tam giác ABC. Bán kính mặt cầu ngoại tiếp khối chóp G.A'B'C' bằng:
 Xem đáp án
Xem đáp án
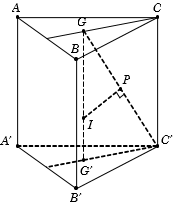
Gọi M là trung điểm B'C', ta có
Trong , có ;
Gọi G' là trọng tâm tam giác đều A'B'C', suy ra G' cũng là tâm đường tròn ngoại tiếp
Vì lặng trụ đứng nên
Do đó GG' là trục của tam giác A'B'C'
Trong mặt phẳng (GC'G'), kẻ trung trực d của đoạn thẳng GC' cắt GG' tại I. Khi đó I là tâm mặt cầu ngoại tiếp khối chóp G.A'B'C', bán kính R = GI
Ta có
Câu 33:
là phương trình của mặt cầu khi và chỉ khi:
 Xem đáp án
Xem đáp án
Chọn B
là phương trình của một mặt cầu khi và chỉ khi (1)
Mà nên (1) đòi hỏi d < 0
Câu 35:
Cho hai mặt cầu (S) và (S’) lần lượt có tâm I và J, bán kính R và R’. Đặt d = IJ. Câu nào sau đây sai?
I. và (S') trong nhau
II. và (S') ngoài nhau
III. và (S') tiếp xúc ngoài
IV. và (S') tiếp xúc trong Xem đáp án
Xem đáp án
Chọn D
và (S') ngoài nhau
và (S') cắt nhau
và (S') tiếp xúc trong
và (S') tiếp xúc ngoài.
Vậy cả 4 mệnh đề đều sai.
Câu 36:
 Xem đáp án
Xem đáp án
Hai câu A và B đúng
Câu 37:
Cho mặt cầu và mặt phẳng
I. cắt (S)
II. tiếp xúc (S)
III. không cắt (S) Xem đáp án
Xem đáp án
Câu 38:
 Xem đáp án
Xem đáp án
Chọn A
Thử 4 đáp án, ở đây thầy thử trước đáp án A nhé
NhậpCâu 39:
Với điều kiện nào của m thì mặt phẳng cong sau là mặt cầu?
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
(S) là mặt cầu
Câu 40:
 Xem đáp án
Xem đáp án
Chọn D
Ta có:
là mặt cầu
Câu 41:
Giá trị t phải thỏa mãn điều kiện nào để mặt cong sau là mặt cầu:
 Xem đáp án
Xem đáp án
Chọn D
Ta có:
(S) là mặt cầu
Câu 42:
Tìm tập hợp các tâm I của mặt cầu
 Xem đáp án
Xem đáp án
Chọn B
Ta có:
Tâm
Vậy tập hợp các điểm I là phân đường thẳng tương ứng với
Câu 43:
 Xem đáp án
Xem đáp án
Chọn A
Tâm
tiếp xúc (S) khi:
(loại)
Câu 47:
Hai mặt cầu ;
 Xem đáp án
Xem đáp án
Chọn D
Tâm I(1,3,-2) ; bán kính R = 3
Tâm K(3,-1,2); bán kính R' = 4
=> (S) và (S') cắt nhau.
Câu 48:
 Xem đáp án
Xem đáp án
Chọn C
Tâm I(2,-3,5) bán kinh R = 7
Tâm J(1,-1,3), bán kính R' = 4
(S) và (S') tiếp xúc trong
Câu 49:
 Xem đáp án
Xem đáp án
Chọn A
(S) có tâm I(-2,1,-3); pháp vecto của (P)
Câu 50:
 Xem đáp án
Xem đáp án
Chọn D
Phương trình của
(S') qua
Câu 51:
 Xem đáp án
Xem đáp án
là điểm chung của hai mặt cầu
Câu 52:
 Xem đáp án
Xem đáp án
Chọn C
thuộc họ (chùm) mặt cầu có phương trình
Câu 53:
Cho mặt cầu . Viết phương trình tổng quát của đường kính AB song song với đường thẳng
 Xem đáp án
Xem đáp án
Chọn B
Tâm I(3,2,2) vecto chỉ phương của
Câu 54:
 Xem đáp án
Xem đáp án
Chọn A
Phương trình giao tuyến của (S) và mặt phẳng (yOz)
Câu 55:
 Xem đáp án
Xem đáp án
Pháp vecto của qua I(3,2,2)
Câu 56:
Cho mặt cầu . Gọi A là giao điểm của (S) và trục y'Oy có tung độ âm. Viết phương trình tổng quát của tiếp diện (Q) của (S) tại A
 Xem đáp án
Xem đáp án
Chọn C
Giao điểm của (S) và trục
(loại)
Tiếp diện tại
Câu 57:
 Xem đáp án
Xem đáp án
Chọn B
qua A, B, C, D
Câu 58:
 Xem đáp án
Xem đáp án
Chọn D
(S) có tâm I(-2,m,-2m), bán kính
Hình chiếu A của I trên z’Oz là tiếp điểm của (S) và z’Oz
Ta có:
Câu 59:
 Xem đáp án
Xem đáp án
Chọn A
(S) có tâm I(3,-2,-1), bán kính R = 9
(S') có tâm J(1,2,3) bán kính
(S) và (S') tiếp xúc trong
Câu 60:
 Xem đáp án
Xem đáp án
(S) có tâm I(2,1,-3), bán kính
Câu 63:
 Xem đáp án
Xem đáp án
Chọn C
Với và
Câu 64:
 Xem đáp án
Xem đáp án
Chọn D
(P) và (Q) cắt y'Oy lần lượt tại A(0,3,0) và B(0,-5,0)
Tâm I(0,-1,0). Bán kính
Câu 65:
 Xem đáp án
Xem đáp án
Chọn A
Bán kính
Câu 66:
 Xem đáp án
Xem đáp án
Chọn C
(S) có tâm I(2,1,1), bán kính R = 4. Tiếp điểm của (S) có phương trình:
Câu 67:
Viết phươngng trình mặt cầu (S) tâm I(4,2,-1) nhận đường thẳng (D): làm tiếp tuyến.
 Xem đáp án
Xem đáp án
Chọn B
(D) qua A(2,-1,1) có vecto chỉ phương
Câu 68:
 Xem đáp án
Xem đáp án
Chọn D
(S) có tâm I(1,1,2), bán kính R = 2. Phương trình tiếp diện của (S) qua
(P) tiếp xúc
Câu 69:
 Xem đáp án
Xem đáp án
Chọn A
(S') có tâm J(1,-2,4), bán kính
Gọi R là bán kính của (S). (S) và (S') tiếp xúc trong khi và chỉ khi:
(loại)
Câu 70:
 Xem đáp án
Xem đáp án
Chọn D
(P) cắt ba trục Ox, Oy, Oz tại
nên:
Vậy
Câu 71:
 Xem đáp án
Xem đáp án
Chọn D
(S) có tâm I(-1,1,-3), bán kính R = 4. IM vuông góc với (Q), nên IM // (P) => M nằm trong mặt phẳng (R) qua I và song song với (P).
Phương trình
Tập hợp các điểm M là đường tròn giao tuyến của (S) và (R):
Câu 72:
 Xem đáp án
Xem đáp án
Chọn D
(S') có bán kính nhỏ nhất <=> Tâm
Vậy
Câu 73:
 Xem đáp án
Xem đáp án
Chọn C
=> Mặt cầy tiếp xúc với 6 cạnh tại trung điểm của chúng.
Gọi I và J là trung điểm của AB và CD
có bán kính tâm
Câu 74:
 Xem đáp án
Xem đáp án
Chọn B
Tứ diện ABCD đều.
tiếp xúc với bốn mặt của tứ diện tại trọng tâm của mỗi mặt.
Trọng tâm G của tam giác đều ACD: tâm của
Bán kính của
Câu 75:
 Xem đáp án
Xem đáp án
Chọn A
Tứ diện ABCD đều có tâm E(2,2,2)
Bán kính
Câu 76:
Viết phương trình mặt cầu (S) qua ba điểm A(2,0,1); B(1,3,2); C(3,2,0) có tâm nằm trong mặt phẳng (xOy)
 Xem đáp án
Xem đáp án
Chọn C
vì tâm
Câu 77:
 Xem đáp án
Xem đáp án
Chọn D
có tâm I là trung điểm chung của 4 đường chéo: , bán kính
Câu 78:
 Xem đáp án
Xem đáp án
Chọn B
có tâm là trung điểm của 3 đoạn nối trung điểm các mặt đối diện đôi một có độ dài cạnh bằng 1. Bán kính
Câu 79:
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có trùng với ba trục . Viết phương trình mặt cầu ( S3 ) tiếp xúc với tất cả các cạnh của hình lập phương.
 Xem đáp án
Xem đáp án
Chọn A
tiếp xúc với 12 cạnh của hình lập phương tại trung điểm của mỗi cạnh. Tâm là trung điểm chng của 6 đoạn nối trung điểm của các cặp cạnh đối diện đôi một có độ dài bằng
Bán kính
Câu 80:
 Xem đáp án
Xem đáp án
Chọn D
Sáu mặt chéo trên cắt nhau từng đôi một theo các giao tuyến là 4 đường chéo của hình lập phương có chung trung điểm . Ta có 6 phần là 6 hình chóp đều bằng nhau và có đỉnh chung I và đáy là các mặt của hình lập phương.
Câu 81:
Cho hai điểm A(2,-3,-2); B(-4,5,-3). Tìm tập hợp các điểm M(x, y, z) sao cho
 Xem đáp án
Xem đáp án
Chọn B
<=> Mặt cầu
Câu 82:
Cho hai điểm A(2,-3,-1); B(-4,5,-3). Tìm tập hợp các điểm M(x, y, z) thỏa mãn
 Xem đáp án
Xem đáp án
Chọn C
<=> Mặt cầu
Câu 83:
Cho hai điểm A(2,-3,-1); B()-4,5,-3. Tìm tập hợp các điểm M(x, y, z) thỏa mãn
 Xem đáp án
Xem đáp án
Chọn D
Mặt cầ
Câu 84:
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
(S) là mặt cầu
Với
Câu 85:
Cho ba điểm A(1,0,1); B(2,-1,0); C(0,-3,-1). Tìm tập hợp các điểm M(x, y, z) thỏa mãn
 Xem đáp án
Xem đáp án
Chọn A
<=> Mặt cầu
Câu 86:
Cho tứ diện OABC với A(-4,0,0); B(0,6,0); C(0,0,-8). Mặt cầu (S) ngoại tiếp từ diện có tâm và bán kính là:
 Xem đáp án
Xem đáp án
Chọn C
Tâm I của mặt cầu (S) có hình chiếu trên Ox, Oy, Oz lần lượt là trung điểm của OA, OB và OC.
Bán kính
Câu 87:
 Xem đáp án
Xem đáp án
Chọn B
Tâm
đường thẳng (D):
(S) là mặt cầu
Vậy tập hợp các tâm O là phần đường thẳng tương ứng với
Câu 89:
Tìm tập hợp các tâm I của mặt cầu (S): ,
 Xem đáp án
Xem đáp án
Chọn D
Tâm
Vậy tập hợp các tâm I là elip
Câu 90:
 Xem đáp án
Xem đáp án
Chọn B
Tâm cách đều (P) và (Q)
=> Hai mặt phẳng:
Câu 91:
Tìm tập các tâm I của mặt cầu (S) tiếp xúc với hai mặt phẳng
 Xem đáp án
Xem đáp án
Chọn A
Gọi A(-4,0,0) và B(6,0,0) lần lượt là giao điểm của trục x’Ox với (P) và (Q). Trung điểm E(1,0,0) của AB cách đều (P) và (Q).
Tâm I cách đều (P) và (Q) => EI nằm trong mặt (R) qua E song song và cách đều (P) và (Q) ((P)//(Q)).
VậyCâu 92:
 Xem đáp án
Xem đáp án
Chọn C
=> Tập hợp các tâm I của hai mặt phẳng song song và cách đều (P) một đoạn bằng 3:
Câu 94:
 Xem đáp án
Xem đáp án
Câu 95:
 Xem đáp án
Xem đáp án
Chọn D
Mặt cầu (S) ngoại tiếp hình hợp chữ nhật có tâm là trung điêm rchung của 4 đường chéo bằng nhau của hình hộp và có đườg chéo bằng đường chéo. (Học sinh tự vẽ hình)
đvdt
Câu 96:
 Xem đáp án
Xem đáp án
Chọn B
Hai mặt phẳng: x - 2z và x + 2z - 4 = 0 chia hình hộp chữ nhật thành 4 phần bằng nhau. Mặt phẳng y - 3 = 0 cắt 4 phần trên thành 8 phần bằng nhau. (Học sinh tự vẽ hình).
Câu 97:
 Xem đáp án
Xem đáp án
Chọn A
Mặt cầu
Câu 98:
Cho mặt cầu (S): và điểm A(-6,-1,3). Gọi M là tiếp điểm của (S) và tiếp tuyến di động (d) qua A. Tìm tập hợp các điểm M.
 Xem đáp án
Xem đáp án
Chọn D
có tâm
đường tròn
HayCâu 99:
 Xem đáp án
Xem đáp án
Chọn C
Diện tích thiết diện
Là góc tạ bởi và
Câu 100:
 Xem đáp án
Xem đáp án
cắt
=> Hai giao điểm
Câu 101:
Cho tứ diện ABCD có A(3, 6, -2); B(6, 0, 1); C(-1, 2, 0); D(0, 4, 1). Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ :
 Xem đáp án
Xem đáp án
Chọn B
Gọi I(x, y, z) là tâm cầu ngoại tiếp tứ diện ABCD. Tọa độ của I là nghiệm của hệ phương trình :
Câu 102:
 Xem đáp án
Xem đáp án
Chọn B
Phương trình mặt cầu (S) được viết lại :
Và R = 1
Câu 103:
Trong không gian Oxyz cho đường tròn: . Tọa độ tâm H của (C) là:
 Xem đáp án
Xem đáp án
Chọn A
Tâm mặt cầu là
Xem đường thẳng qua I và vuông góc với mặt phẳng thiết diện
, thế x, y, z vào phương trình mặt phẳng thiết diện
Tọa độ tâm H của (C) là
Câu 104:
Trong không gian cho đường tròn . Bán kính r của đường tròn (C) bằng :
 Xem đáp án
Xem đáp án
Chọn C
Cùng đề trên nên có bán kính mặt cầu (C) là
Khoảng cách từ I đến thiết diện là
=> Bán kính của (C) là :
Câu 105:
Trong không gian Oxyz cho đường tròn . Bán kính r của (C) bằng:
 Xem đáp án
Xem đáp án
Chọn C
Viết lại phương trình mặt cầu (S) chứa (C):
Để biết tâm I(1,2,3) và bán kính R = 9
=> Bán kính của (C) là (do khoảng cách từ I đến mặt phẳng chứa (C) là
Câu 106:
 Xem đáp án
Xem đáp án
Chọn B
Viết lại phương trình mặt cầu (S) chứa (C): để biết tâm I(6, -2, 3) và R = 5.
Phương trình đường thẳng qua I và vuông góc với mặt phẳng chứa
Thế vào phương trình mặt phẳng thiết diện:
Câu 107:
Trong không gian Oxyz cho đường tròn . Bán kính r của đường tròn (C) bằng :
 Xem đáp án
Xem đáp án
Chọn D
Cùng đền với Câu 33 nên mặt cầu (S) chứa (C) có tâm I(6, -2, 3) và R = 5.
Khoảng cách từ I đến mặt phẳng thiết diện là:
Câu 108:
Trong không gian Oxyz cho đường tròn (C) có tâm H và bán kính r bằng:
 Xem đáp án
Xem đáp án
Chọn B
Khoảng cách từ I đến mặt phẳng thiết diện là:
Đường thẳng qua tâm của (S) và và vuông góc với mặt phẳng thiết diện có phương trình tham số:
Thế vào phương trình mặt phẳng thiết diện được t = 1 => Tâm H(1,0,1)
Câu 109:
Cho mặt cầu và ba điểm A(1,2,-2); B(-4,2,3); C(1,-3,3) nằm trên mặt cầu (S). Bán kính r của đường tròn ngoại tiếp tam giác ABC là :
 Xem đáp án
Xem đáp án
Chọn C
Cùng đề với câu trên nên khoảng cách từ h từ I đến (ABC):
