39 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 12 Tích phân hàm ẩn có đáp án (Mới nhất)

Câu 1:

Cho hàm số $f (x) = \{\begin{cases} e^{2 x} & k h i x \geq 0 \\ x^{2} + x + 2 & k h i x < 0 \end{cases}$ . Biết tích phân $\int_{- 1}^{1} f (x) d x = \frac{a}{b} + \frac{e^{2}}{c}$ ( $\frac{a}{b}$ là phân số tối giản). Giá trị $a + b + c$ bằng

A. 7

B. 8

C. 9

D. 10

Xem đáp án

Chọn C
Ta có:

I = \int_{- 1}^{1} f (x) dx = \int_{- 1}^{0} (x^{2} + x + 2) d x + \int_{0}^{1} e^{2 x} d x = \frac{4}{3} + \frac{e^{2}}{2}

.
Vậy

a + b + c = 9

.

Câu 2:

Cho hàm số $f (x) = \{\begin{cases} x (1 + x^{2}) & k h i x \geq 3 \\ \frac{1}{x - 4} & k h i x < 3 \end{cases}$ . Tích phân $\int_{e^{2}}^{e^{4}} \frac{f (\ln x)}{x} d x$ bằng:

A. $\frac{40}{3} - \ln 2$

B. $\frac{95}{6} + \ln 2$

C. $\frac{189}{4} + \ln 2$

D. $\frac{189}{4} - \ln 2$

Xem đáp án

Chọn D

Xét $I = \int_{e^{2}}^{e^{4}} \frac{f (\ln x)}{x} d x$

Đặt $t = \ln x \Rightarrow d t = \frac{1}{x} d x$

Đổi cận: $\begin{array}{l} x = e^{2} \Rightarrow t = 2 \\ x = e^{4} \Rightarrow t = 4 \end{array}$ .

I = \int_{2}^{4} f (t) d t = \int_{2}^{4} f (x) d x = \int_{2}^{3} \frac{1}{x - 4} d x + \int_{3}^{4} x (1 + x^{2}) d x = \frac{189}{4} - \ln 2

.

Câu 3:

Cho hàm số $f (x) = \{\begin{cases} \frac{1}{x} & k h i x \geq 1 \\ x + 1 & k h i x < 1 \end{cases}$ . Tích phân $\int_{- 2}^{1} f (\sqrt[3]{1 - x}) d x = \frac{m}{n}$ ( $\frac{m}{n}$ là phân số tối giản), khi đó $m - 2 n$ bằng:

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Chọn A

Xét $I = \int_{- 7}^{1} f (\sqrt[3]{1 - x}) d x$

Đặt $t = \sqrt[3]{1 - x} \Rightarrow - 3 t^{2} d t = d x$

Đổi cận: $\begin{array}{l} x = - 7 \Rightarrow t = 2 \\ x = 1 \Rightarrow t = 0 \end{array}$ .

$I = - 3 \int_{2}^{0} t^{2} f (t) d t = 3 \int_{0}^{2} x^{2} f (x) d x = 3 [\int_{0}^{1} x^{2} (x + 1) d x + \int_{1}^{2} x d x] = \frac{25}{12}$ .

Câu 4:

Cho hàm số $f (x)$ liên tục trên R và $\int_{0}^{1} f (x) d x = 4$ , $\int_{0}^{3} f (x) d x = 6$ . Tính $I = \int_{- 1}^{1} f (|2 x + 1|) d x$

A. $I = 3$

B. I=5

C. I=6

D. I=4

Xem đáp án

Chọn B

Đặt $u = 2 x + 1$ $\Rightarrow d x = \frac{1}{2} d u$ . Khi $x = - 1$ thì $u = - 1$ . Khi $x = 1$ thì $u = 3$ .

Nên $I = \frac{1}{2} \int_{- 1}^{3} f (|u|) d u$ $= \frac{1}{2} (\int_{- 1}^{0} f (|u|) d u + \int_{0}^{3} f (|u|) d u)$

$= \frac{1}{2} (\int_{- 1}^{0} f (- u) d u + \int_{0}^{3} f (u) d u)$ .

Xét $\int_{0}^{1} f (x) d x = 4$ . Đặt $x = - u$ $\Rightarrow d x = - d u$ .

Khi $x = 0$ thì $u = 0$ . Khi $x = 1$ thì $u = - 1$ .

Nên $4 = \int_{0}^{1} f (x) d x = - \int_{0}^{- 1} f (- u) d u = \int_{- 1}^{0} f (- u) d u$ .

Ta có $\int_{0}^{3} f (x) d x = 6 \Rightarrow \int_{0}^{3} f (u) d u = 6$ .

Nên $I = \frac{1}{2} (\int_{- 1}^{0} f (- u) d u + \int_{0}^{3} f (u) d u) = \frac{1}{2} (4 + 6) = 5$

Câu 5:

Cho

F (x)

là một nguyên hàm của hàm số

f (x) = |1 + x| - |1 - x|

trên tập R và thỏa mãn

F (1) = 3

. Tính tổng

F (0) + F (2) + F (- 3)

A. 8

B. 12

C. 14

D. 10

Xem đáp án

Chọn C

Bảng khử dấu giá trị tuyệt đối:

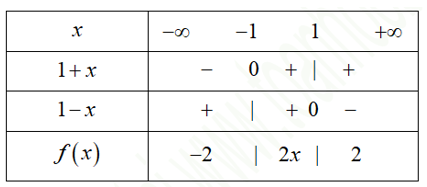
Cho F(x) là một nguyên hàm của hàm số f(x)=|1+x|-|1-x| trên tập R và thỏa mãn F(1)=3 . Tính tổng F(0)+F(2)+F(-3) (ảnh 1)

Ta có: $\int_{1}^{2} f (x) d x = F (2) - F (1) = F (2) - 3$ mà $\int_{1}^{2} f (x) d x = \int_{1}^{2} 2 d x = 2$ nên $F (2) = 5$ .

Ø $\int_{0}^{1} f (x) d x = F (1) - F (0) = 3 - F (0)$ mà $\int_{0}^{1} f (x) d x = \int_{0}^{1} 2 x d x = x^{2} |_{0}^{1} = 1$ nên $F (0) = 2$ .

Ø $\int_{- 1}^{0} f (x) d x = F (0) - F (- 1) = 2 - F (- 1)$ mà $\int_{- 1}^{0} f (x) d x = \int_{- 1}^{0} 2 x d x = x^{2} |_{- 1}^{0} = - 1$ nên $F (- 1) = 3$ .

Ø $\int_{- 3}^{- 1} f (x) d x = F (- 1) - F (- 3) = 3 - F (- 3)$ mà $\int_{- 3}^{- 1} f (x) d x = \int_{- 3}^{- 1} - 2 d x = - 4$ nên $F (- 3) = 7$ .

Vậy $F (0) + F (2) + F (- 3) = 2 + 5 + 7 = 14$ .

Câu 6:

Biết $I = \int_{1}^{5} \frac{2 |x - 2| + 1}{x} d x = 4 + a \ln 2 + b \ln 5$ với $a, b \in ℤ$ . Tính $S = a + b$ .

A. $S = 9$

B. $S = 11$

C. $S = - 3$

D. $S = 5$

Xem đáp án

Chọn D

Ta có $|x - 2| = \{\begin{cases} x - 2 khi x \geq 2 \\ 2 - x khi x \leq 2 \end{cases}$ .

Do đó $I = \int_{1}^{2} \frac{2 |x - 2| + 1}{x} d x + \int_{2}^{5} \frac{2 |x - 2| + 1}{x} d x$ .

$= \int_{1}^{2} \frac{2 (2 - x) + 1}{x} d x + \int_{2}^{5} \frac{2 (x - 2) + 1}{x} d x = \int_{1}^{2} (\frac{5}{x} - 2) d x + \int_{2}^{5} (2 - \frac{3}{x}) d x$ .

$= (5 \ln |x| - 2 x) |\begin{matrix} 2 \\ 1 \end{matrix} + (2 x - 3 \ln |x|) |\begin{matrix} 5 \\ 2 \end{matrix} = 4 + 8 \ln 2 - 3 \ln 5$

$\Rightarrow \{\begin{cases} a = 8 \\ b = - 3 \end{cases}$ $\Rightarrow S = a + b = 5$

Câu 7:

Cho hàm số $f (x)$ có đạo hàm liên tục trên R thỏa mãn $f (x^{3} + 3 x + 1) = 3 x + 2$ , với mọi $x \in ℝ$ .Tích phân $\int_{1}^{5} x f^{'} (x) d x$ bằng

A. $- \frac{31}{4}$

B. $\frac{17}{4}$

C. $\frac{33}{4}$

D. $\frac{49}{4}$

Xem đáp án

Chọn C

Từ giả thiết ta có $f (x^{3} + 3 x + 1) = 3 x + 2$ nên suy ra $f (1) = 2$ , $f (5) = 5$ .

Suy ra $I = \int_{1}^{5} x f^{'} (x) d x = {x f (x)|}_{1}^{5} - \int_{1}^{5} f (x) d x = 23 - \int_{1}^{5} f (x) d x$ .

Đặt $x = t^{3} + 3 t + 1 \Rightarrow d x = (3 t^{2} + 3) d t$ .

Với $x = 1 \Rightarrow t = 0; x = 5 \Rightarrow t = 1$

Do đó $\int_{1}^{5} f (x) d x = \int_{0}^{1} f (t^{3} + 3 t + 1) (3 t^{2} + 3) d t = \int_{0}^{1} (3 t + 2) (3 t^{2} + 3) d t = \frac{59}{4}$ .

Vậy $I = 23 - \frac{59}{4} = \frac{33}{4}$ .

Câu 8:

Cho hàm số $y = f (x)$ xác định và liên tục trên R thoả $f (x^{5} + 4 x + 3) = 2 x + 1, \forall x \in ℝ .$ Tích phân $\int_{- 2}^{8} f (x) d x$ bằng

A. 2

B. 10

C. $\frac{32}{3}$

D. 72

Xem đáp án

Chọn B

Đặt $x = t^{5} + 4 t + 3 \Rightarrow d x = (5 t^{4} + 4) d t$ .

Đổi cận: $\{\begin{cases} x = - 2 \Rightarrow t = - 1 \\ x = 8 \Rightarrow t = 1 \end{cases}$

Khi đó

\int_{- 2}^{8} f (x) d x = \int_{- 1}^{1} f (t^{5} + 4 t + 3) (5 t^{4} + 4) d t = \int_{- 1}^{1} (2 t + 1) (5 t^{4} + 4) d t = 10

.

Câu 9:

Cho hàm số $f (x)$ xác định $ℝ \ \{\frac{1}{2}\},$ thỏa $f^{'} (x) = \frac{2}{2 x - 1}, f (0) = 1$ và $f (1) = 2.$ Giá trị của biểu thức $f (- 1) + f (3)$ bằng

A. $\ln 15.$

B. $2 + \ln 15.$

C. $3 + \ln 15.$

D. $4 + \ln 15.$

Xem đáp án

Chọn C

Ta có $f^{'} (x) = \frac{2}{2 x - 1}$

$\frac{2}{2 x - 1} d x = \ln |2 x - 1| + C = \{\begin{cases} \ln (1 - 2 x) + C_{1}; x < \frac{1}{2} \\ \ln (2 x - 1) + C_{2}; x > \frac{1}{2} \end{cases}$

$f (0) = 1 \Rightarrow C_{1} = 1$ và $f (1) = 2 \Rightarrow C_{2} = 2$ .

Do đó $f (x) = \{\begin{cases} \ln (1 - 2 x) + 1; x < \frac{1}{2} \\ \ln (2 x - 1) + 2; x > \frac{1}{2} \end{cases} \Rightarrow \{\begin{cases} f (- 1) = \ln 3 + 1 \\ f (3) = \ln 5 + 2 \end{cases}$

$\Rightarrow f (- 1) + f (3) = 3 + \ln 15.$

Câu 10:

Cho hàm số $f (x) = \{\begin{cases} 3 x^{2} + 2 x & khi x \geq 0 \\ 5 - x & khi x < 0 \end{cases}$ . Khi đó $I = \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos x f (\sin x) d x$ bằng

A. $\frac{15}{2}$

B. 15

C. 8

D. $\frac{17}{2}$

Xem đáp án

Chọn A

Đặt $t = \sin x \Rightarrow d t = \cos x d x$ . Đổi cận $\{\begin{cases} x = - \frac{π}{2} \Rightarrow t = - 1 \\ x = \frac{π}{2} \Rightarrow t = 1 \end{cases}$ .

$\Rightarrow I = \int_{- 1}^{1} f (t) d t = \int_{- 1}^{1} f (x) d x$

Do $f (x) = \{\begin{cases} 3 x^{2} + 2 x & khi x \geq 0 \\ 5 - x & khi x < 0 \end{cases}$

$\Rightarrow I = \int_{- 1}^{0} (5 - x) d x + \int_{0}^{1} (3 x^{2} + 2 x) d x = \frac{15}{2}$ .

Câu 11:

Cho hàm số

f (x) = \{\begin{cases} x^{2} - 2 x + 3 & khi x \geq 2 \\ x + 1 & khi x < 2 \end{cases}

. Khi đó

I = \int_{0}^{1} f (3 - 2 x) d x

bằng

A. $\frac{41}{2}$

B. 21

C. $\frac{41}{12}$

D. $\frac{41}{21}$

Xem đáp án

Chọn C

Đặt $t = 3 - 2 x \Rightarrow d t = - 2 d x \Rightarrow d x = - \frac{1}{2} d t$ . Đổi cận $\{\begin{cases} x = 0 \Rightarrow t = 3 \\ x = 1 \Rightarrow t = 1 \end{cases}$ .

Do $f (x) = \{\begin{cases} x^{2} - 2 x + 3 & khi x \geq 2 \\ x + 1 & khi x < 2 \end{cases}$

\Rightarrow I = \frac{1}{2} (\int_{1}^{2} (x + 1) d x + \int_{2}^{3} (x^{2} - 2 x + 3) d x) = \frac{41}{12}

.

Câu 12:

Cho hàm số $f (x) = \{\begin{cases} x^{2} + 2 x & khi x \geq \frac{3}{2} \\ x - 2 & khi x < \frac{3}{2} \end{cases}$ . Khi đó $I = \int_{0}^{\frac{π}{2}} \sin x f (\cos x + 1) d x$ bằng

A. $\frac{35}{12}$

B. 3

C. $\frac{19}{4}$

D. $\frac{10}{3}$

Xem đáp án

Chọn A

Đặt $t = \cos x + 1 \Rightarrow d t = - \sin x d x$ . Đổi cận $\{\begin{cases} x = 0 \Rightarrow t = 2 \\ x = \frac{π}{2} \Rightarrow t = 1 \end{cases}$ .

$\Rightarrow I = \int_{1}^{2} f (t) d t = \int_{1}^{2} f (x) d x$

Do $f (x) = \{\begin{cases} x^{2} + 2 x & khi x \geq \frac{3}{2} \\ x - 2 & khi x < \frac{3}{2} \end{cases}$

$\Rightarrow I = \int_{1}^{\frac{3}{2}} (x - 2) d x + \int_{\frac{3}{2}}^{2} (x^{2} + 2 x) d x = \frac{35}{12}$ .

Câu 13:

Cho hàm số $f (x) = \{\begin{cases} x^{2} - x & khi x \geq 0 \\ x & khi x < 0 \end{cases}$ . Khi đó $I = \int_{- \frac{π}{2}}^{\frac{π}{2}} \cos x f (\sin x) d x$ bằng

A. $- \frac{2}{3}$

B. $- 1$

C. $- \frac{1}{3}$

D. $- \frac{4}{3}$

Xem đáp án

Chọn A

Đặt $t = \sin x \Rightarrow d t = \cos x d x$ . Đổi cận $\{\begin{cases} x = - \frac{π}{2} \Rightarrow t = - 1 \\ x = \frac{π}{2} \Rightarrow t = 1 \end{cases}$ .

$\Rightarrow I = \int_{- 1}^{1} f (t) d t = \int_{- 1}^{1} f (x) d x$

Do $f (x) = \{\begin{cases} x^{2} - x & khi x \geq 0 \\ x & khi x < 0 \end{cases}$

$\Rightarrow I = \int_{- 1}^{0} x d x + \int_{0}^{1} (x^{2} - x) d x = - \frac{2}{3}$ .

Câu 14:

Cho hàm số $f (x) = \{\begin{cases} x^{2} + x + 1 & khi x \geq 3 \\ 2 x - 1 & khi x < 3 \end{cases}$ . Khi đó $I = \int_{0}^{2} x f (x^{2} + 1) d x$ bằng

A. 24

B. $\frac{73}{3}$

C. $\frac{74}{3}$

D. 23

Xem đáp án

Chọn B

Đặt $t = x^{2} + 1 \Rightarrow d t = 2 x d x \Rightarrow x d x = \frac{1}{2} d t$ . Đổi cận $\{\begin{cases} x = 0 \Rightarrow t = 1 \\ x = 2 \Rightarrow t = 5 \end{cases}$ .

$\Rightarrow I = \frac{1}{2} \int_{1}^{5} f (t) d t = \frac{1}{2} \int_{1}^{5} f (x) d x$

Do $f (x) = \{\begin{cases} x^{2} + x + 1 & khi x \geq 3 \\ 2 x - 1 & khi x < 3 \end{cases}$

$\Rightarrow I = \frac{1}{2} (\int_{1}^{3} (2 x - 1) d x + \int_{3}^{5} (x^{2} + x + 1) d x) = \frac{73}{3}$ .

Câu 15:

Cho hàm số $f (x) = \{\begin{cases} 3 x + 3 khi x < \frac{1}{2} \\ x + 4 khi x \geq \frac{1}{2} \end{cases}$ . Tính tích phân $\int_{0}^{\frac{π}{2}} f (\sin x) \cos x d x$ .

A. 8

B. $\frac{17}{4}$

C. $\frac{13}{2}$

D. $\frac{21}{5}$

Xem đáp án

Chọn B

Xét $I = \int_{0}^{\frac{π}{2}} f (\sin x) \cos x d x$

Đặt $\sin x = t \Rightarrow \cos x d x = d t$

Với $x = 0 \Rightarrow t = 0$

$x = \frac{π}{2} \Rightarrow t = 1$

$I = \int_{0}^{1} f (t) d t = \int_{0}^{1} f (x) d x = \int_{0}^{\frac{1}{2}} f (x) d x + \int_{\frac{1}{2}}^{1} f (x) d x = \int_{0}^{\frac{1}{2}} (3 x + 3) d x + \int_{\frac{1}{2}}^{1} (x + 4) d x = \frac{17}{4} .$

Câu 16:

Cho hàm số $f (x) = \{\begin{cases} 2 x^{2} + 1 khi x \geq 0 \\ 2 x^{2} - x + 1 khi x < 0 \end{cases}$ . Tính tích phân $\int_{0}^{\frac{π}{3}} f (3 \cos x - 2) \sin x d x$ .

A. $\frac{33}{2}$

B. $\frac{15}{23}$

C. 12

D. $\frac{19}{24}$

Xem đáp án

Chọn D

Xét $I = \int_{0}^{\frac{π}{3}} f (3 \cos x - 2) \sin x d x$

Đặt $3 \cos x - 2 = t \Rightarrow - 3 \sin x d x = d t \Rightarrow \sin x d x = - \frac{1}{3} d t$

Với $x = 0 \Rightarrow t = 0$

$x = \frac{π}{3}$ $\Rightarrow t = - \frac{1}{2}$

$I = \frac{1}{3} \int_{- \frac{1}{2}}^{1} f (t) d t = \frac{1}{3} \int_{- \frac{1}{2}}^{1} f (x) d x = \frac{1}{3} \int_{- \frac{1}{2}}^{0} f (x) d x + \frac{1}{3} \int_{0}^{1} f (x) d x$

$= \frac{1}{3} \int_{- \frac{1}{2}}^{0} (2 x^{2} - x + 1) d x + \frac{1}{3} \int_{0}^{1} (2 x^{2} + 1) d x = \frac{19}{24} .$

Câu 17:

Cho hàm số $f (x) = \{\begin{cases} 1 - x^{2} khi x \leq 1 \\ 2 x - 2 khi x > 1 \end{cases}$ . Tính tích phân $\int_{- \frac{π}{2}}^{\frac{π}{4}} f (5 \sin 2 x - 1) \cos 2 x d x$ .

A. $\frac{11}{10}$

B. $\frac{43}{31}$

C. $\frac{31}{30}$

D. $\frac{31}{10}$

Xem đáp án

Chọn C

Xét $I = \int_{- \frac{π}{2}}^{\frac{π}{4}} f (5 \sin 2 x - 1) \cos 2 x d x$

Đặt $5 \sin 2 x - 1 = t \Rightarrow 10 \cos 2 x d x = d t \Rightarrow \cos 2 x d x = \frac{1}{10} d t$

Với $x = - \frac{π}{2} \Rightarrow t = - 1$

$x = \frac{π}{4} \Rightarrow t = 4$

$\Rightarrow I = \frac{1}{10} \int_{- 1}^{4} f (t) d t = \frac{1}{10} \int_{- 1}^{4} f (x) d x = \frac{1}{10} \int_{- 1}^{1} f (x) d x + \frac{1}{10} \int_{1}^{4} f (x) d x$

$= \frac{1}{10} \int_{- 1}^{1} (1 - x^{2}) d x + \frac{1}{10} \int_{1}^{4} (2 x - 2) d x = \frac{31}{30} .$

Câu 18:

Cho hàm số $f (x) = \{\begin{cases} 2 x^{3} - x - 5 khi x \geq 2 \\ 11 - x khi x < 2 \end{cases}$ . Tính tích phân $\int_{\frac{1}{e}}^{e} f (2 + \ln x) \frac{1}{x} d x$ .

A. $\frac{69}{2}$

B. 12

C. $\frac{25}{2}$

D. 30

Xem đáp án

Chọn A

Xét $I = \int_{1}^{e} f (2 + \ln x) \frac{1}{x} d x$

Đặt $2 + \ln x = t \Rightarrow \frac{1}{x} d x = d t$

Với $x = \frac{1}{e} \Rightarrow t = 1$

$x = e \Rightarrow t = 3$

$\Rightarrow I = \int_{1}^{3} f (t) d t = \int_{1}^{3} f (x) d x = \int_{1}^{2} f (x) d x + \int_{2}^{3} f (x) d x = \int_{1}^{2} (11 - x) d x + \int_{2}^{3} (2 x^{3} - x - 5) d x = \frac{69}{2} .$

Câu 19:

Cho hàm số $f (x) = \{\begin{cases} 1 - x^{2} khi x \leq 3 \\ 7 - 5 x khi x > 3 \end{cases}$ . Tính tích phân $\int_{0}^{\ln 2} f (3 e^{x} - 1) e^{x} d x$ .

A. $\frac{13}{15}$

B. $- \frac{102}{33}$

C. $- \frac{94}{9}$

D. $\frac{25}{9}$

Xem đáp án

Chọn C

Xét $I = \int_{0}^{\ln 2} f (3 e^{x} - 1) e^{x} d x$

Đặt $3 e^{x} - 1 = t \Rightarrow 3 e^{x} d x = d t \Rightarrow e^{x} d x = \frac{1}{3} d t$

Với $x = 0 \Rightarrow t = 2$

$x = \ln 2 \Rightarrow t = 5$

$\Rightarrow I = \frac{1}{3} \int_{2}^{5} f (t) d t = \frac{1}{3} \int_{2}^{3} f (x) d x + \frac{1}{3} \int_{3}^{5} f (x) d x = \frac{1}{3} \int_{2}^{3} (1 - x^{2}) d x + \frac{1}{3} \int_{3}^{5} (7 - 5 x) d x = - \frac{94}{9} .$

Câu 20:

Giá trị của tích phân $\int_{0}^{\frac{π}{2}} max \{\sin x, \cos x\} d x$ bằng

A. 0

B. 1

C. $\sqrt{2}$

D. $\frac{1}{\sqrt{2}}$

Xem đáp án

Chọn C

Ta có phương trình $\sin x - \cos x = 0$ có một nghiệm trên đoạn $[0; \frac{π}{2}]$ là $x = \frac{π}{4}$ .

Bảng xét dấu

Giá trị của tích phân bi/ 2 đến 0 max{sinx,cosx}dx bằng (ảnh 1)

Suy ra

\int_{0}^{\frac{π}{2}} \max \{\sin x, \cos x\} d x = \int_{0}^{\frac{π}{4}} \cos x d x + \int_{\frac{π}{4}}^{\frac{π}{2}} \sin x d x

= {(\sin x)|}_{0}^{\frac{π}{4}} - {(\cos x)|}_{\frac{π}{4}}^{\frac{π}{2}} = \sqrt{2}

.

Câu 21:

Tính tích phân $I = \int_{0}^{2} \max \{x^{3}, x\} d x$ .

A. $\frac{9}{4}$

B. $\frac{17}{4}$

C. $\frac{19}{4}$

D. $\frac{14}{4}$

Xem đáp án

Chọn B

Đặt $f (x) = x^{3} - x$ ta có bảng xét dấu sau:

$Tính tích phân I=tích phân 2 đến 0 max{x^3,x}dx . (ảnh 1)$

Dựa vào bảng xét dấu ta có.

$\forall x \in [0; 1], f (x) \leq 0 \Leftrightarrow x^{3} - x \leq 0 \Leftrightarrow x^{3} \leq x \Rightarrow \max \{x^{3}, x\} = x$ .

$\forall x \in [1; 2], f (x) \geq 0 \Leftrightarrow x^{3} - x \geq 0 \Leftrightarrow x^{3} \geq x \Rightarrow \max \{x^{3}, x\} = x^{3}$ .

Ta có: $I = \int_{0}^{2} \max \{x^{3}, x\} d x = \int_{0}^{1} \max \{x^{3}, x\} d x + \int_{1}^{2} \max \{x^{3}, x\} d x$ .

Nên $I = \int_{0}^{2} \max \{x^{3}, x\} d x = \int_{0}^{1} x d x + \int_{1}^{2} x^{3} d x = {\frac{1}{2} x^{2}|}_{0}^{1} + {\frac{1}{4} x^{4}|}_{1}^{2} = \frac{17}{4}$ .

Câu 22:

Cho hàm số $y = f (x)$ liên tục trên $ℝ \ \{0; - 1\}$ thỏa mãn $\{\begin{cases} f (1) = - 2 \ln 2 \\ f (2) = a + b \ln 3; a, b \in ℚ \\ x (x + 1) . f^{'} (x) + f (x) = x^{2} + x \end{cases}$ .Tính $a^{2} + b^{2}$

A. $\frac{25}{4}$

B. $\frac{9}{2}$

C. $\frac{5}{2}$

D. $\frac{13}{4}$

Xem đáp án

Chọn B

Ta có $x (x + 1) . f^{'} (x) + f (x) = x^{2} + x$ (1)

Chia cả 2 vế của biểu thức (1) cho ${(x + 1)}^{2}$ ta được $\frac{x}{x + 1} . f^{'} (x) + \frac{1}{{(x + 1)}^{2}} f (x) = \frac{x}{x + 1}$

$\Rightarrow {[\frac{x}{x + 1} . f (x)]}^{'} = \frac{x}{x + 1}$ , với $\forall x \in ℝ \ \{0; - 1\}$ $\Rightarrow \frac{x}{x + 1} . f (x) = \int \frac{x}{x + 1} d x$ .

Mặt khác, $f (1) = - 2 \ln 2 \Leftrightarrow 2 (1 - \ln 2 + C) = - 2 \ln 2 \Leftrightarrow C = - 1$ .

Do đó $f (x) = \frac{x + 1}{x} (x - \ln |x + 1| - 1)$ .

Với $x = 2$ thì $f (x) = \frac{3}{2} (1 - \ln 3) = \frac{3}{2} - \frac{3}{2} \ln 3$ . Suy ra $a = \frac{3}{2}$ và $b = - \frac{3}{2}$ .

Vậy $a^{2} + b^{2} = \frac{9}{2}$ .

Câu 23:

Cho hàm số $y = f (x)$ có đạo hàm trên R thỏa mãn $\{\begin{cases} f (0) = f^{'} (0) = 1 \\ f (x + y) = f (x) + f (y) + 3 x y (x + y) - 1 \end{cases}$ với $x, y \in ℝ$ . Tính $\int_{0}^{1} f (x - 1) d x$ .

A. $\frac{1}{2}$

B. $\frac{1}{4}$

C. $\frac{- 1}{4}$

D. $\frac{7}{4}$

Xem đáp án

Chọn C

Lấy đạo hàm theo hàm số

$f^{'} (x + y) = f^{'} (y) + 3 x^{2} + 6 x y$ , $\forall x \in ℝ$ .

Cho $y = 0 \Rightarrow f^{'} (x) = f^{'} (0) + 3 x^{2} \Rightarrow f^{'} (x) = 1 + 3 x^{2}$

$\Rightarrow f (x) = \int f^{'} (x) d x = x^{3} + x + C$ mà $f (0) = 1 \Rightarrow C = 1$ . Do đó $f (x) = x^{3} + x + 1$ .

Vậy $\int_{0}^{1} f (x - 1) d x = \int_{- 1}^{0} f (x) d x = \int_{- 1}^{0} (x^{3} + x + 1) d x = \frac{1}{4}$ .

Câu 24:

Cho hàm số $f (x)$ có đạo hàm liên tục trên $[0; 1]$ thỏa mãn $f (1) = 0$ , $\int_{0}^{1} {[f^{'} (x)]}^{2} d x = 7$ và $\int_{0}^{1} x^{2} f (x) d x = \frac{1}{3}$ . Tích phân $\int_{0}^{1} f (x) d x$ bằng

A. $\frac{7}{5}$

B. 1

C. $\frac{7}{4}$

D. 4

Xem đáp án

Chọn A

Ta có $\int_{0}^{1} x^{2} f (x) d x = {[\frac{x^{3}}{3} f (x)]|}_{0}^{1} - \int_{0}^{1} \frac{x^{3}}{3} f^{'} (x) d x$ . Suy ra $\int_{0}^{1} \frac{x^{3}}{3} f^{'} (x) d x = - \frac{1}{3}$ .

Hơn nữa ta dễ dàng tính được $\int_{0}^{1} \frac{x^{6}}{9} d x = \frac{1}{63}$ .

Do đó $\int_{0}^{1} {[f^{'} (x)]}^{2} d x + 2.21 \int_{0}^{1} \frac{x^{3}}{3} f^{'} (x) d x + 21^{2} \int_{0}^{1} \frac{x^{6}}{9} d x = 0$ $\Leftrightarrow \int_{0}^{1} {[f^{'} (x) + 7 x^{3}]}^{2} d x = 0$ .

Suy ra $f^{'} (x) = - 7 x^{3}$ , do đó $f (x) = - \frac{7}{4} x^{4} + C$ . Vì $f (1) = 0$ nên $C = \frac{7}{4}$ .

Vậy $\int_{0}^{1} f (x) d x = - \frac{7}{4} \int_{0}^{1} (x^{4} - 1) d x = \frac{7}{5}$ .

Câu 25:

Xét hàm số

f (x)

có đạo hàm liên tục trên R và thỏa mãn điều kiện

f (1) = 1

và

f (2) = 4

. Tính

J = \int_{1}^{2} (\frac{f^{'} (x) + 2}{x} - \frac{f (x) + 1}{x^{2}}) d x

.

A. $J = 1 + \ln 4$

B. $J = 4 - \ln 2$

C. $J = \ln 2 - \frac{1}{2}$

D. $J = \frac{1}{2} + \ln 4$

Xem đáp án

Chọn D

Ta có $J = \int_{1}^{2} (\frac{f^{'} (x) + 2}{x} - \frac{f (x) + 1}{x^{2}}) d x = \int_{1}^{2} \frac{f^{'} (x)}{x} d x - \int_{1}^{2} \frac{f (x)}{x^{2}} d x + \int_{1}^{2} (\frac{2}{x} - \frac{1}{x^{2}}) d x$ .

Đặt $\{\begin{cases} u = \frac{1}{x} \\ d v = f^{'} (x) d x \end{cases} \Rightarrow \{\begin{cases} d u = - \frac{1}{x^{2}} d x \\ v = f (x) \end{cases}$ .

$J = \int_{1}^{2} (\frac{f^{'} (x) + 2}{x} - \frac{f (x) + 1}{x^{2}}) d x$ $= {\frac{1}{x} . f (x)|}_{1}^{2} + \int_{1}^{2} \frac{f (x)}{x^{2}} d x - \int_{1}^{2} \frac{f (x)}{x^{2}} d x + \int_{1}^{2} (\frac{2}{x} - \frac{1}{x^{2}}) d x$ .

$= \frac{1}{2} f (2) - f (1) + {(2 \ln x + \frac{1}{x})|}_{1}^{2} = \frac{1}{2} + \ln 4$

Câu 26:

Cho hàm số $f (x)$ xác định trên $ℝ \ \{- 2; 1\}$ thỏa mãn

$f^{'} (x) = \frac{1}{x^{2} + x - 2}, f (- 3) - f (3) = 0, f (0) = \frac{1}{3}$ . Giá trị của biểu thức $f (- 4) + f (1) - f (4)$ bằng

A. $\frac{1}{3} \ln 20 + \frac{1}{3}$

B. $\frac{1}{3} \ln 2 + \frac{1}{3}$

C. $\ln 80 + 1$

D. $\frac{1}{3} \ln \frac{8}{5} + 1$

Xem đáp án

Chọn B

Ta có: $f^{'} (x) = \frac{1}{x^{2} + x - 2} = \frac{1}{3} (\frac{1}{x - 1} - \frac{1}{x + 2})$

$f (x) = \frac{1}{3} \int (\frac{1}{x - 1} - \frac{1}{x + 2}) d x = \frac{1}{3} \ln |\frac{x - 1}{x + 2}| + C = \{\begin{cases} \frac{1}{3} [\ln (1 - x) - \ln (- x - 2)] + C_{1}; x \in (- \infty; - 2) \\ \frac{1}{3} [\ln (1 - x) - \ln (x + 2)] + C_{2}; x \in (- 2; 1) \\ \frac{1}{3} [\ln (x - 1) - \ln (x + 2)] + C_{3}; x \in (1; + \infty) \end{cases}$

Với $f (0) = \frac{1}{3} \Rightarrow \frac{1}{3} [\ln (1 - 0) - \ln (0 + 2)] + C_{2} = \frac{1}{3} \Rightarrow C_{2} = \frac{1}{3} \ln 2 + \frac{1}{3}$

Với $f (- 3) - f (3) = 0 \Rightarrow C_{1} - C_{3} = \frac{1}{3} \ln \frac{1}{10}$

Nên $f (- 4) + f (1) - f (4) = \frac{1}{3} \ln \frac{5}{2} + \frac{1}{3} \ln 2 - \frac{1}{3} \ln \frac{1}{2} + C_{2} + C_{1} - C_{3} = \frac{1}{3} \ln 2 + \frac{1}{3}$ .

Câu 27:

Cho hàm số $f (x)$ xác định và liên tục trên R đồng thời thỏa mãn $\{\begin{cases} f (x) > 0, \forall x \in ℝ \\ f^{'} (x) = - e^{x} f^{2} (x), \forall x \in ℝ \\ f (0) = \frac{1}{2} \end{cases} .$

Tính giá trị của $f (\ln 2)$ .

A. $f (\ln 2) = \frac{1}{4}$

B. $f (\ln 2) = \frac{1}{3}$

C. $f (\ln 2) = \ln 2 + \frac{1}{2}$

D. $f (\ln 2) = \ln^{2} 2 + \frac{1}{2}$

Xem đáp án

Chọn B

Ta có $f^{'} (x) = - e^{x} f^{2} (x) \Leftrightarrow \frac{f^{'} (x)}{f^{2} (x)} = - e^{x}$ ( do $f (x) > 0$ )

$\Rightarrow \int \frac{f^{'} (x)}{f^{2} (x)} d x = \int - e^{x} d x \Rightarrow - \frac{1}{f (x)} = - e^{x} + C \Rightarrow f (x) = \frac{1}{e^{x} - C}$ .

Mà $f (0) = \frac{1}{2} \Rightarrow \frac{1}{e^{0} - C} = \frac{1}{2} \Rightarrow C = - 1$ .

$\Rightarrow f (x) = \frac{1}{e^{x} + 1} \Rightarrow f (\ln 2) = \frac{1}{e^{\ln 2} + 1} = \frac{1}{3}$ .

Câu 28:

Cho hai hàm $f (x)$ và $g (x)$ có đạo hàm trên $[1; 4]$ , thỏa mãn $\{\begin{matrix} f (1) + g (1) = 4 \\ g (x) = - x f^{'} (x) \\ f (x) = - x g^{'} (x) \end{matrix}$ với mọi $x \in [1; 4]$ . Tính tích ph $I = \int_{1}^{4} [f (x) + g (x)] d x$ .

A. $3 \ln 2$

B. $4 \ln 2$

C. $6 \ln 2$

D. $8 \ln 2$

Xem đáp án

Chọn D

Từ giả thiết ta có $f (x) + g (x) = - x . f^{'} (x) - x . g^{'} (x)$

$\Leftrightarrow [f (x) + x . f^{'} (x)] + [g (x) + x . g^{'} (x)] = 0$ $\Leftrightarrow {[x . f (x)]}^{'} + {[x . g (x)]}^{'} = 0$

$\Rightarrow x . f (x) + x . g (x) = C \Rightarrow f (x) + g (x) = \frac{C}{x}$

Mà $f (1) + g (1) = 4 \Rightarrow C = 4 \Rightarrow I = \int_{1}^{4} [f (x) + g (x)] d x = \int_{1}^{4} \frac{4}{x} d x = 8 \ln 2$ .

Câu 29:

Cho hai hàm $f (x)$ và $g (x)$ có đạo hàm trên $[1; 2]$ thỏa mãn $f (1) = g (1) = 0$ và $\{\begin{cases} \frac{x}{{(x + 1)}^{2}} g (x) + 2017 x = (x + 1) f^{'} (x) \\ \frac{x^{3}}{x + 1} g^{'} (x) + f (x) = 2018 x^{2} \end{cases}, \forall x \in [1; 2] .$

Tính tích phân $I = \int_{1}^{2} [\frac{x}{x + 1} g (x) - \frac{x + 1}{x} f (x)] d x$ .

A. $I = \frac{1}{2}$

B. $I = 1$

C. $I = \frac{3}{2}$

D. I=2

Xem đáp án

Chọn A

Từ giả thiết ta có: $\{\begin{cases} \frac{1}{{(x + 1)}^{2}} g (x) - \frac{x + 1}{x} f^{'} (x) = - 2017 \\ \frac{x}{x + 1} g^{'} (x) + \frac{1}{x^{2}} f (x) = 2018 \end{cases}, \forall x \in [1; 2] .$

Suy ra: $\begin{array}{l} [\frac{1}{{(x + 1)}^{2}} g (x) + \frac{x}{x + 1} g^{'} (x)] - [\frac{x + 1}{x} f^{'} (x) - \frac{1}{x^{2}} f (x)] = 1 \Leftrightarrow {[\frac{x}{x + 1} g (x)]}^{'} - {[\frac{x + 1}{x} f (x)]}^{'} = 1 \\ \Rightarrow \frac{x}{x + 1} g (x) - \frac{x + 1}{x} f (x) = x + C . \end{array}$

Mà $f (1) = g (1) = 0 \Rightarrow C = - 1 \Rightarrow I = \int_{1}^{2} [\frac{x}{x + 1} g (x) - \frac{x + 1}{x} f (x)] d x = \int_{1}^{2} (x - 1) d x = \frac{1}{2} .$

Câu 30:

Cho hàm số $f (x) = \{\begin{cases} x^{3} + x + 2 khi x < 1 \\ x + 3 khi x \geq 1 \end{cases}$ . Tính tích phân $\int_{0}^{\frac{π}{2}} f (3 \sin^{2} x - 1) \sin 2 x d x$ .

A. $\frac{21}{4}$

B. $\frac{13}{2}$

C. $\frac{20}{3}$

D. $\frac{5}{6}$

Xem đáp án

Chọn A

Xét $I = \int_{0}^{\frac{π}{2}} f (3 \sin^{2} x - 1) \sin 2 x d x$

Đặt $3 \sin^{2} x - 1 = t \Rightarrow 3 \sin 2 x d x = d t \Rightarrow \sin 2 x d x = \frac{1}{3} d t$

Với $x = 0 \Rightarrow t = - 1$

$x = \frac{π}{2} \Rightarrow t = 2$

$\Rightarrow I = \frac{1}{3} \int_{- 1}^{2} f (t) d t = \frac{1}{3} \int_{- 1}^{2} f (x) d x = \frac{1}{3} \int_{- 1}^{1} f (x) d x + \frac{1}{3} \int_{1}^{2} f (x) d x$

$= \frac{1}{3} \int_{- 1}^{1} (x^{3} + x + 2) d x + \frac{1}{3} \int_{1}^{2} (x + 3) d x = \frac{21}{4} .$ .

Câu 31:

Cho hàm số $f (x) = \{\begin{cases} 2 x - 1 khi x \geq 1 \\ x^{2} khi x < 1 \end{cases}$ . Tính tích phân $\int_{1}^{13} f (\sqrt{x + 3} - 2) d x$ .

A. $- \frac{231}{5}$

B. $\frac{97}{6}$

C. $\frac{16}{3}$

D. $\frac{113}{3}$

Xem đáp án

Chọn B

Xét $I = \int_{1}^{13} f (\sqrt{x + 3} - 2) d x$

Đặt $\sqrt{x + 3} - 2 = t \Rightarrow \sqrt{x + 3} = t + 2 \Rightarrow x + 3 = {(t + 2)}^{2} \Rightarrow d x = 2 (t + 2) d t$

Với $x = 1 \Leftrightarrow t = 0$

$x = 13 \Leftrightarrow t = 2$

$\Rightarrow I = 2 \int_{0}^{2} (t + 2) f (t) d t = 2 \int_{0}^{2} (x + 2) f (x) d x = 2 \int_{0}^{1} (x + 2) f (x) d x + 2 \int_{1}^{2} (x + 2) f (x) d x$

$= 2 \int_{0}^{1} (x + 2) x^{2} d x + 2 \int_{1}^{2} (2 x - 1) (x + 2) d x = \frac{97}{6} .$

Câu 32:

Cho hàm số $f (x) = \{\begin{cases} 2 x - 4 khi x \geq 2 \\ 4 - 2 x khi x < 2 \end{cases}$ . Tính tích phân $\int_{- \frac{π}{4}}^{\frac{π}{2}} f (3 - 4 \cos^{2} x) \sin 2 x d x$ .

A. $\frac{2}{3}$

B. $\frac{1}{2}$

C. $\frac{21}{4}$

D. $\frac{5}{12}$

Xem đáp án

Chọn A

Xét $I = \int_{- \frac{π}{4}}^{\frac{π}{2}} f (3 - 4 \cos^{2} x) \sin 2 x d x$

Đặt $3 - 4 \cos^{2} x = t \Rightarrow \sin 2 x d x = \frac{1}{4} d t$

Với $x = - \frac{π}{4} \Rightarrow t = 1$

$x = \frac{π}{2} \Rightarrow t = 3$

$\Rightarrow I = \frac{1}{4} \int_{1}^{3} f (t) d t = \frac{1}{4} \int_{1}^{3} f (x) d x = \frac{1}{4} \int_{1}^{2} f (x) d x + \frac{1}{4} \int_{2}^{3} f (x) d x$

$= \frac{1}{3} \int_{1}^{2} (4 - 2 x) d x + \frac{1}{3} \int_{2}^{3} (2 x - 4) d x = \frac{2}{3} .$

Câu 33:

Cho hàm số $f (x) = \{\begin{cases} x^{4} + 2 x^{2} - 1 khi x < 1 \\ 3 - x^{2} khi x \geq 1 \end{cases}$ . Tính tích phân $\int_{1}^{e^{4}} f (\sqrt{4 - \ln x}) \frac{1}{x} d x$ .

A. $\frac{16}{3}$

B. 17

C. $\frac{11}{6}$

D. $\frac{6}{11}$

Xem đáp án

Chọn C

Xét $I = \int_{1}^{e^{4}} f (\sqrt{4 - \ln x}) \frac{1}{x} d x$

Đặt $\sqrt{4 - \ln x} = t \Rightarrow 4 - \ln x = t^{2} \Rightarrow \frac{1}{x} d x = - 2 t d t$

Với $x = 1 \Rightarrow t = 2$

$x = e^{4} \Rightarrow t = 0$

$\Rightarrow I = 2 \int_{0}^{2} t . f (t) d t = 2 \int_{0}^{2} x . f (x) d x = 2 \int_{0}^{1} x . f (x) d x + 2 \int_{1}^{2} x . f (x) d x$

$= 2 \int_{0}^{1} x (x^{4} + 2 x^{2} - 1) d x + 2 \int_{1}^{2} x (3 - x^{2}) d x = \frac{11}{6} .$ .

Câu 34:

Cho hàm số

f (x) = \{\begin{cases} 2 x^{2} - 1 khi x < 0 \\ x - 1 khi 0 \leq x \leq 2 \\ 5 - 2 x khi x > 2 \end{cases}

. Tính tích phân

\int_{- \frac{π}{4}}^{\frac{π}{4}} f (2 - 7 \tan x) \frac{1}{\cos^{2} x} d x

.

A. $\frac{201}{77}$

B. $\frac{34}{103}$

C. $\frac{155}{7}$

D. $\frac{109}{21}$

Xem đáp án

Chọn D

Xét $I = \int_{- \frac{π}{4}}^{\frac{π}{4}} f (2 - 7 \tan x) \frac{1}{\cos^{2} x} d x$

Đặt $2 - 7 \tan x = t \Rightarrow \frac{1}{\cos^{2} x} d x = - \frac{1}{7} d t$

Với $x = - \frac{π}{4} \Rightarrow t = 9$

$x = \frac{π}{4} \Rightarrow t = - 5$

$\Rightarrow I = \frac{1}{7} \int_{- 5}^{9} f (t) d t = \frac{1}{7} \int_{- 5}^{9} f (x) d x = \frac{1}{7} \int_{- 5}^{0} f (x) d x + \frac{1}{7} \int_{0}^{2} f (x) d x + \frac{1}{7} \int_{2}^{9} f (x) d x$

$= \frac{1}{7} \int_{- 5}^{0} (2 x^{2} - 1) d x + \frac{1}{7} \int_{0}^{2} (x - 1) d x + \frac{1}{7} \int_{2}^{9} (5 - 2 x) d x = \frac{109}{21} .$

Câu 35:

Cho hàm số $f (x) = \{\begin{cases} x^{2} - x & khi x \geq 0 \\ x & khi x < 0 \end{cases}$ . Khi đó $I = 2 \int_{0}^{\frac{π}{2}} \cos x f (\sin x) d x + 2 \int_{0}^{2} f (3 - 2 x) d x$ bằng

$A . \frac{7}{3}$

B. $\frac{8}{3}$

C. 3

D. $\frac{10}{3}$

Xem đáp án

Chọn D

Ta có: $I = 2 \int_{0}^{\frac{π}{2}} \cos x f (\sin x) d x + 2 \int_{0}^{2} f (3 - 2 x) d x = I_{1} + I_{2}$

Đặt $t = \sin x \Rightarrow d t = \cos x d x$ . Đổi cận $\{\begin{cases} x = 0 \Rightarrow t = 0 \\ x = \frac{π}{2} \Rightarrow t = 1 \end{cases}$ .

$\Rightarrow I_{1} = 2 \int_{0}^{1} f (t) d t = \int_{- 1}^{1} f (t) d t = \int_{- 1}^{1} f (x) d x$

Do $f (x) = \{\begin{cases} x^{2} - x & khi x \geq 0 \\ x & khi x < 0 \end{cases}$

$\Rightarrow I_{1} = \int_{- 1}^{0} x d x + \int_{0}^{1} (x^{2} - x) d x = - \frac{2}{3} V$ .

Đặt $t = 3 - 2 x \Rightarrow d t = - 2 d x \Rightarrow d x = - \frac{1}{2} d t$ . Đổi cận $\{\begin{cases} x = 0 \Rightarrow t = 3 \\ x = 2 \Rightarrow t = - 1 \end{cases}$ .

$\Rightarrow I_{2} = \int_{- 1}^{3} f (t) d t = \int_{- 1}^{3} f (x) d x$

Do $f (x) = \{\begin{cases} x^{2} - x & khi x \geq 0 \\ x & khi x < 0 \end{cases}$

$\Rightarrow I_{2} = (\int_{- 1}^{0} x d x + \int_{0}^{3} (x^{2} - x) d x) = 4$ .

Vậy $I = I_{1} + I_{2} = \frac{10}{3}$

Câu 36:

Cho hàm số $f (x) = \{\begin{cases} 4 x & khi x > 2 \\ - 2 x + 12 & khi x \leq 2 \end{cases}$ . Tính tích phân $I = \int_{0}^{\sqrt{3}} \frac{x . f (\sqrt{x^{2} + 1})}{\sqrt{x^{2} + 1}} d x + \int_{\ln 2}^{\ln 3} e^{2 x} . f (1 + e^{2 x}) d x$

A. 84

B. 83

C. 48

D. -84

Xem đáp án

Chọn A

Ta có: $I = \int_{0}^{\sqrt{3}} \frac{x . f (\sqrt{x^{2} + 1})}{\sqrt{x^{2} + 1}} d x + \int_{\ln 2}^{\ln 3} e^{2 x} . f (1 + e^{2 x}) d x = I_{1} + I_{2}$

Đặt $t = \sqrt{x^{2} + 1} \Rightarrow t^{2} = x^{2} + 1 \Rightarrow 2 t d t = 2 x d x \Rightarrow x d x = t d t$ . Đổi cận $\{\begin{cases} x = 0 \Rightarrow t = 1 \\ x = \sqrt{3} \Rightarrow t = 2 \end{cases}$ .

$\Rightarrow I_{1} = \int_{1}^{2} f (t) d t = \int_{1}^{2} f (t) d t = \int_{1}^{2} f (x) d x$

Do $f (x) = \{\begin{cases} 4 x & khi x > 2 \\ - 2 x + 12 & khi x \leq 2 \end{cases}$

$\Rightarrow I_{1} = \int_{1}^{2} (- 2 x + 12) d x = 9$ .

Đặt $t = 1 + e^{2 x} \Rightarrow d t = 2 e^{2 x} d x \Rightarrow e^{2 x} d x = \frac{1}{2} d t$ . Đổi cận $\{\begin{cases} x = \ln 2 \Rightarrow t = 5 \\ x = \ln 3 \Rightarrow t = 10 \end{cases}$ .

$\Rightarrow I_{2} = \frac{1}{2} \int_{5}^{10} f (t) d t = \frac{1}{2} \int_{5}^{10} f (x) d x$

Do $f (x) = \{\begin{cases} 4 x & khi x > 2 \\ - 2 x + 12 & khi x \leq 2 \end{cases}$

$\Rightarrow I_{2} = \frac{1}{2} \int_{5}^{10} 4 x = 75$ .

Vậy $I = I_{1} + I_{2} = 84$

Câu 37:

Cho hàm số $f (x) = \{\begin{cases} 2 x^{3} - x & khi x \geq 1 \\ - 3 x + 2 & khi x < 1 \end{cases}$ . Biết $I = \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{f (\tan x)}{\cos^{2} x} d x + \int_{0}^{\sqrt{\sqrt{e} - 1}} \frac{x . f (\ln (x^{2} + 1))}{x^{2} + 1} d x = \frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản. Giá trị của tổng a+b bằng

A. 69

B. 68

C. 67

D. 66

Xem đáp án

Chọn A

$I = \int_{\frac{π}{4}}^{\frac{π}{3}} \frac{f (\tan x)}{\cos^{2} x} d x + \int_{0}^{\sqrt{\sqrt{e} - 1}} \frac{x . f (\ln (x^{2} + 1))}{x^{2} + 1} d x = I_{1} + I_{2}$

Đặt $t = \tan x \Rightarrow d t = \frac{1}{\cos^{2} x} d x$ . Đổi cận $\{\begin{cases} x = \frac{π}{4} \Rightarrow t = 1 \\ x = \frac{π}{3} \Rightarrow t = \sqrt{3} \end{cases}$ .

$\Rightarrow I_{1} = \int_{1}^{\sqrt{3}} f (t) d t = \int_{1}^{\sqrt{3}} f (x) d x$

Đặt $t = \ln (x^{2} + 1) \Rightarrow d t = \frac{2 x}{x^{2} + 1} d x \Rightarrow \frac{x}{x^{2} + 1} d x = \frac{1}{2} d t$ . Đổi cận $\{\begin{cases} x = 0 \Rightarrow t = 0 \\ x = \sqrt{\sqrt{e} - 1} \Rightarrow t = \frac{1}{2} \end{cases}$ .

$\Rightarrow I_{2} = \frac{1}{2} \int_{0}^{\frac{1}{2}} f (t) d t = \frac{1}{2} \int_{0}^{\frac{1}{2}} f (x) d x$

Do $f (x) = \{\begin{cases} 2 x^{3} - x & khi x \geq 1 \\ - 3 x + 2 & khi x < 1 \end{cases}$

$\Rightarrow I = I_{1} + I_{2} = \int_{1}^{\sqrt{3}} (2 x^{3} - x) d x + \frac{1}{2} \int_{0}^{\frac{1}{2}} (- 3 x + 2) d x = \frac{53}{16} \Rightarrow a = 53, b = 16$ .

Vậy $a + b = 69$

Câu 38:

Cho hàm số $f (x) = \{\begin{cases} \frac{1}{2} x + 2 & khi 0 \leq x<2 \\ - x + 7 & khi 2 \leq x < 5 \end{cases}$ . Biết $I = \int_{1}^{e^{2}} \frac{f (\ln x)}{x} d x + \int_{\sqrt{3}}^{2 \sqrt{6}} x . f (\sqrt{x^{2} + 1}) d x = \frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản. Giá trị của hiệu a-b bằng

A. 77

B. 67

C. 57

D. 76

Xem đáp án

Chọn A

$I = \int_{1}^{e^{2}} \frac{f (\ln x)}{x} d x + \int_{\sqrt{3}}^{2 \sqrt{6}} x . f (\sqrt{x^{2} + 1}) d x = I_{1} + I_{2}$

Đặt $t = \ln x \Rightarrow d t = \frac{1}{x} d x$ . Đổi cận $\{\begin{cases} x = 1 \Rightarrow t = 0 \\ x = e^{2} \Rightarrow t = 2 \end{cases}$ .

$\Rightarrow I_{1} = \int_{0}^{2} f (t) d t = \int_{0}^{2} f (x) d x$

Đặt $t = \sqrt{x^{2} + 1} \Rightarrow t^{2} = x^{2} + 1 \Rightarrow 2 t d t = 2 x d x \Rightarrow x d x = t d t$ . Đổi cận $\{\begin{cases} x = \sqrt{3} \Rightarrow t = 2 \\ x = 2 \sqrt{6} \Rightarrow t = 5 \end{cases}$ .

$\Rightarrow I_{2} = \int_{2}^{5} t . f (t) d t = \int_{2}^{5} x . f (x) d x$

Do $f (x) = \{\begin{cases} \frac{1}{2} x + 2 & khi 0 \leq x<2 \\ - x + 7 & khi 2 \leq x < 5 \end{cases}$

$\Rightarrow I = I_{1} + I_{2} = \int_{0}^{2} (\frac{1}{2} x + 2) d x + \int_{2}^{5} x . (- x + 7) d x = \frac{79}{2} \Rightarrow a = 79, b = 2$ .

Vậy $a - b = 77$

Câu 39:

Cho hàm số $f (x) = \{\begin{cases} x^{2} + x + 1 & khi x \geq 0 \\ 2 x - 3 & khi x < 0 \end{cases}$ . Biết $I = \int_{0}^{\frac{π}{2}} f (2 \sin x - 1) \cos x d x + \int_{e}^{e^{2}} \frac{f (\ln x)}{x} d x = \frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản. Giá trị của tích a+b bằng

A. 305

B. -305

C. 350

D. -350

Xem đáp án

Chọn B

$I = \int_{0}^{\frac{π}{2}} f (2 \sin x - 1) \cos x d x + \int_{e}^{e^{2}} \frac{f (\ln x)}{x} d x = I_{1} + I_{2}$

Đặt $t = 2 \sin x - 1 \Rightarrow d t = 2 \cos x d x \Rightarrow \cos x d x = \frac{d t}{2}$ . Đổi cận $\{\begin{cases} x = 0 \Rightarrow t = - 1 \\ x = \frac{π}{2} \Rightarrow t = 1 \end{cases}$ .

$\Rightarrow I_{1} = \frac{1}{2} \int_{- 1}^{1} f (t) d t = \frac{1}{2} \int_{- 1}^{1} f (x) d x$

Do $f (x) = \{\begin{cases} x^{2} + x + 1 & khi x \geq 0 \\ 2 x - 3 & khi x < 0 \end{cases}$

$\Rightarrow I = \frac{1}{2} (\int_{- 1}^{0} (2 x - 3) d x + \int_{0}^{1} (x^{2} + x + 1) d x) = - \frac{13}{12}$ .

Đặt $t = \ln x \Rightarrow d t = \frac{1}{x} d x$ . Đổi cận $\{\begin{cases} x = e \Rightarrow t = 1 \\ x = e^{2} \Rightarrow t = 2 \end{cases}$ .

$\Rightarrow I_{2} = \int_{1}^{2} f (t) d t = \int_{1}^{2} f (x) d x$

Do $f (x) = \{\begin{cases} x^{2} + x + 1 & khi x \geq 0 \\ 2 x - 3 & khi x < 0 \end{cases}$

$\Rightarrow I = \int_{1}^{2} (x^{2} + x + 1) d x = \frac{29}{6}$ .

$\Rightarrow I = I_{1} + I_{2} = - \frac{377}{72} \Rightarrow a = - 377, b = 72$

Vậy $a + b = - 305$