25 câu hỏi trắc nghiệm thuộc 200 Bài tập nguyên hàm tích phân cơ bản, nâng cao (P1) - vietjack.online

200 bài trắc nghiệm nguyên hàm tích phân cơ bản, nâng cao cơ lời giải chi tiết

200 Bài tập nguyên hàm tích phân cơ bản, nâng cao (P1)

7989 lượt thi
25 câu hỏi
50 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Biết $\int f (x - 1) d x = \frac{x - 1}{x + 1}$ +c và $\int f (x + 1) d x = F (x) + c$ thì

Đáp án D.

$Ta có : \int f (x - 1) dx = \frac{x - 1}{x + 1} + C \Leftrightarrow f (x - 1) = \frac{2}{{(x + 1)}^{2}} = \frac{2}{{[(x - 1) + 2]}^{2}} \Rightarrow f (x) = \frac{2}{{(x + 2)}^{2}} \Rightarrow f (x + 1) = \frac{2}{{(x + 1 + 2)}^{2}} = \frac{2}{{(x + 3)}^{2}} \Rightarrow \int f (x + 1) dx = \int \frac{2}{{(x + 3)}^{2}} dx = \frac{- 2}{x + 3} + C \Rightarrow F (x) = \frac{- 2}{x + 3}$

Câu 2:

Biết $\int \frac{\sin 4 x d x}{\sin^{4} x + \cos^{4} x} = F (x) + c$ . Khi đó

Đáp án B.

$\frac{\sin 4 x}{\sin^{4} x + \cos^{4} x} = \frac{2 \sin 2 x \cos 2 x}{1 - 2 \sin^{2} x \cos^{2} x} = \frac{2 \sin 2 x \cos 2 x}{1 - 2 . \frac{1}{4} \sin^{2} 2 x} = \frac{4 \sin 2 x \cos 2 x}{2 - \sin^{2} 2 x} \Rightarrow \int \frac{\sin 4 x d x}{\sin^{4} x + \cos^{4} x} = \int \frac{4 \sin 2 x \cos 2 x d x}{2 - \sin^{2} 2 x} = I Đ ặ t 2 - \sin^{2} 2 x = t \Leftrightarrow - 4 \sin 2 x \cos 2 x d x = d t \Rightarrow I = \int \frac{- d t}{t} = - \ln |t| = - \ln |2 - \sin^{2} 2 x| = \ln |\frac{1}{2 - \sin^{2} 2 x}| = \ln |\frac{1}{\sin^{4} x + \cos^{4} x}| = \ln (\frac{1}{\sin^{4} x + \cos^{4} x}) (d o \frac{1}{\sin^{4} x + \cos^{4} x} > 0)$

Câu 3:

Biết $\int_{0}^{1} f (x) d x = 2 .$ Tính $I = \int_{0}^{1} x f (x^{2}) d x .$

A. I=1.

B. I=4.

C. I= $\frac{1}{2}$

D. I=0.

Đáp án A.

$Đặt x^{2} = t \Leftrightarrow xdx = \frac{dt}{2} Đổi cận x = 0 \Rightarrow t = 0; x = 1 \Rightarrow t = 1 \Rightarrow I = \int_{0}^{1} f (t) . \frac{1}{2} . d t = \frac{1}{2} \int_{0}^{1} f (x) d x = \frac{1}{2} . 2 = 1$

Câu 4:

Biết $\int_{- 1}^{1} \cos a x . \cos b x = 1$ (a,b là hằng số). Tính I= $\int_{- 1}^{1} \frac{\cos a x . \cos b x}{e^{x} + 1} d x .$

A. I=2.

B. I=4.

C. I= $\frac{1}{2}$ .

D. I=1.

Đáp án C.

Câu 5:

Cho f(x) liên tục trên [-2;2] và $\int_{- 2}^{2} f (x) d x = \frac{π}{2}$ . Tính I= $\int_{- 2}^{2} [f (x) - f (- x)] d x .$

A. I= $π$

B. I= $\frac{π}{2}$

C. I= $\frac{π}{4}$

D. I=0.

Đáp án D.

$I = \int_{- 2}^{2} [f (x) - f (- x)] d x = \int_{- 2}^{2} f (x) d x - \int_{- 2}^{2} f (- x) d x = \frac{π}{2} - K Đặt - x = t \Leftrightarrow dx = - dt Đổi cận x = 2 \Rightarrow t = - 2; x = - 2 \Rightarrow t = 2 \Rightarrow K = \int_{2}^{- 2} - f (t) d t = \int_{- 2}^{2} f (t) d t = \int_{- 2}^{2} f (x) d x = \frac{π}{2} \Rightarrow I = 0$

Câu 6:

Cho (C): $x^{2} + {(y - 2)}^{2} = 1$ quay quanh Ox tạo thành khối tròn xoay có thể tích V. Khi đó:

Đáp án C.

$x^{2} + {(y - 2)}^{2} = 1 \Leftrightarrow {(y - 2)}^{2} = 1 - x^{2} \Rightarrow Đ K : 1 - x^{2} > 0 \Leftrightarrow - 1 < x < 1 \Leftrightarrow \{\begin{cases} y = 2 + \sqrt{1 - x^{2}} \\ y = 2 - \sqrt{1 - x^{2}} \end{cases} \Rightarrow V = π \int_{- 1}^{1} [{(2 + \sqrt{1 - x^{2}})}^{2} - {(2 - \sqrt{1 - x^{2}})}^{2}] d x = π \int_{- 1}^{1} 8 \sqrt{1 - x^{2}} d x = 8 π \int_{- 1}^{1} \sqrt{1 - x^{2}} d x$

Câu 7:

Cho D giới hạn bởi y=0, y = f(x) = $x^{3} - 4 x^{2} + x + 6$ thì diện tích D được tính bởi:

Đáp án D.

$X é t P T : x^{3} - 4 x^{2} + x + 6 = 0 \Leftrightarrow \{\begin{cases} x = - 1 \\ x = 3 \\ x = 2 \end{cases} X é t d ấ u b i ể u t h ứ c f (x) = x^{3} - 4 x^{2} + x + 6 t a t h ấ y f (x) > 0 \Leftrightarrow - 1 < x < 2 v à f (x) < 0 \Leftrightarrow 2 < x < 3 \Rightarrow D = \int_{- 1}^{2} f (x) d x - \int_{2}^{3} f (x) d x$

Câu 8:

Biết $\int \frac{d x}{\sqrt{x^{2} + 1}} = F (x) + c$ thì:

Đáp án D.

Câu 9:

Biết $\int cosx . \sin^{6} xdx = F (x) + C$ thì

Đáp án C.

$\int cosx . \sin^{6} xdx = \int \sin^{6} x . d (sinx) = \frac{1}{7} . \sin^{7} x + C \Rightarrow F (x) = \frac{1}{7} . \sin^{7} x$

Câu 10:

Tính tích phân: I= $\int_{0}^{2} | 1 - 2 x | d x$

A. I = $\frac{3}{2}$

B. I=2.

C. I = $\frac{5}{2}$

D. I=3.

Đáp án C.

$Ta có : |1 - 2 x| = \{\begin{cases} 1 - 2 x khi x \leq \frac{1}{2} \\ 2 x - 1 khi x > \frac{1}{2} \end{cases} \Rightarrow I = \int_{0}^{2} |1 - 2 x| d x = \int_{0}^{\frac{1}{2}} (1 - 2 x) d x + \int_{\frac{1}{2}}^{2} (2 x - 1) d x = \frac{1}{4} + \frac{9}{4} = \frac{5}{2}$

Câu 11:

Với các hằng số thực a,b (a<b). Tính $\int_{a}^{b} {(2^{x})}^{2} d x$

Đáp án A.

Câu 12:

Tính diện tích S của miền phẳng D giới hạn bởi y= $e^{x}; y = e^{- x};$ và x=1

Đáp án B.

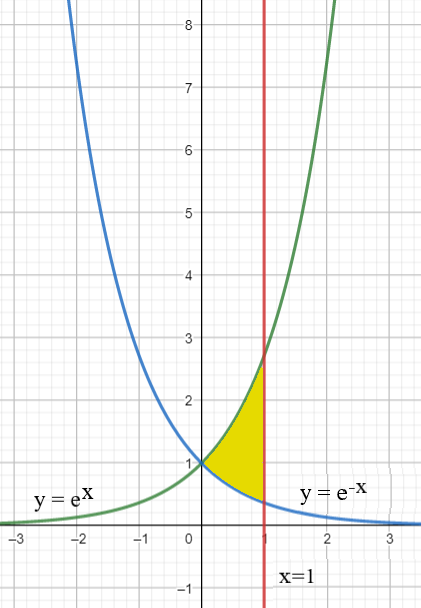
Diện tích hình phẳng cần tính là phần màu vàng như hình vẽ

$Xét PT : e^{x} = e^{- x} \Leftrightarrow x = 0 \Rightarrow S = \int_{0}^{1} (e^{x} - e^{- x}) d x = \int_{0}^{1} e^{x} d x - \int_{0}^{1} e^{- x} d x = e - 1 - (\frac{- 1}{e} + 1) = e + \frac{1}{e} - 2$

Câu 13:

Cho (D): x=0;y=0 và y=x- $π$ quay quanh Ox. Tính thể tích khối tròn xoay được tạo thành:

Đáp án D.

$X é t P T : x - π = 0 \Leftrightarrow x = π$

Câu 14:

Cho f(x)= $\frac{x}{e^{x}}$ thì $\int f (x) d x$ là:

Đáp án C.

$Ta có : I = \int \frac{x}{e^{x}} dx Đặt \{\begin{array}{l} x = u \\ \frac{1}{e^{x}} dx = dv \end{array} \Leftrightarrow \{\begin{cases} dx = du \\ v = - e^{- x} \end{cases} \Rightarrow I = - x . e^{- x} + \int e^{- x} dx = - x . e^{- x} - e^{- x} I = - e^{- x} (x + 1) + C = - \frac{(x + 1)}{e^{x}} + C$

Câu 15:

Biết $\int \cos 2 x \cos x d x = f (x) + c$ thì

Đáp án B.

$\int \cos 2 xcosxdx = \int \frac{1}{2} (\cos 3 x + cosx) dx = \frac{1}{2} (\frac{\sin 3 x}{3} + sinx) + C = \frac{1}{6} \sin 3 x + \frac{1}{2} sinx + C$

Câu 16:

Cho hằng số a>0, tính I= $\int_{- 1}^{a} | x | d x t h e o a$

Đáp án C.

$Ta có : |x| = \{\begin{cases} x nếu x \geq 0 \\ - x nếu x < 0 \end{cases} \Rightarrow I = \int_{- 1}^{a} |x| d x = \int_{- 1}^{0} - x d x + \int_{0}^{a} x d x = \frac{1}{2} + \frac{a^{2}}{2} = \frac{a^{2} + 1}{2}$

Câu 17:

Biết $\int_{1}^{4} e^{\sqrt{x}} d x = 4 e^{2} - e - \frac{1}{2} F (x) d x$ thì F(x) bằng

Đáp án B.

Câu 18:

Tính diện tích S của miền phẳng D ( S_D ) giới hạn bởi: y=0, y= $6 x - 3 x^{2}$

Đáp án D.

$X é t P T : 6 x - 3 x^{2} = 0 \Leftrightarrow \{\begin{cases} x = 0 \\ x = 2 \end{cases} \Rightarrow S = \int_{0}^{2} |6 x - 3 x^{2}| d x = \int_{0}^{2} (6 x - 3 x^{2}) d x = 4 (d o 6 x - 3 x^{2} > 0 v ớ i x \in (0; 2))$

Câu 19:

Biết $\int e^{x} (\sin x + \cos x) d x = F (x) + C$ thì

Đáp án B.

$I = \int e^{x} (sinx + cosx) dx = \int e^{x} sinxdx + \int e^{x} cosxdx = A + B Đặt \{\begin{array}{l} sinx = u \\ e^{x} dx = dv \end{array} \Leftrightarrow \{\begin{cases} cosxdx = du \\ v = e^{x} \end{cases} \Rightarrow A = e^{x} sinx - \int e^{x} cosxdx = e^{x} sinx - B \Rightarrow I = e^{x} sinx - B + B = e^{x} sinx$

Câu 20:

Biết $\int \cos 3 x d x = F (x) + c$ và $F (\frac{π}{6}) = 1$ . Tính $F (\frac{π}{3})$

Đáp án B.

$Ta có : \int \cos 3 xdx = \frac{\sin 3 x}{3} + C \Rightarrow F (\frac{π}{6}) = \frac{\sin (\frac{π}{2})}{3} + C = 1 \Rightarrow C = \frac{2}{3} \Rightarrow F (\frac{π}{3}) = \frac{\sin (π)}{3} + \frac{2}{3} = \frac{2}{3}$

Câu 21:

Tính I= $\int_{- 1}^{1} | 2 x - 1 | d x$

A. I=2.

B. I= $\frac{3}{2}$

C. I=3.

D. I= $\frac{5}{2}$

Đáp án D.

$Ta có : |2 x - 1| = \{\begin{cases} 2 x - 1 nếu x \geq \frac{1}{2} \\ 1 - 2 x nếu x < \frac{1}{2} \end{cases} \Rightarrow \int_{- 1}^{1} |2 x - 1| d x = \int_{- 1}^{\frac{1}{2}} (1 - 2 x) d x + \int_{\frac{1}{2}}^{1} (2 x - 1) d x = \frac{9}{4} + \frac{1}{4} = \frac{5}{2}$

Câu 22:

Tính I= $\int_{1}^{2} e^{x} (\frac{1}{x} \ln x) d x$

Đáp án D.

Câu 23:

Tính diện tích S_D của miền hình phẳng D được giới hạn bởi x=1,y=0, y= $\frac{e^{x} - 1}{e^{x}}$

Đáp án A.

$Xét PT : \frac{e^{x} - 1}{e^{x}} = 0 \Leftrightarrow x = 0 \Rightarrow S_{D} = \int_{0}^{1} (\frac{e^{x} - 1}{e^{x}}) d x = \int_{0}^{1} (1 - \frac{1}{e^{x}}) d x = \int_{0}^{1} d x - \int_{0}^{1} \frac{1}{e^{x}} d x = 1 + \frac{1}{e} - 1 = \frac{1}{e}$

Câu 24:

Tính thể tích của miền phẳng D (phần gạch chéo ở hình vẽ) khi cho D quay quanh trục Ox

Đáp án C.

$Gọi d là đường thẳng đi qua 2 điểm (2; 0) và (1; 1) có dạng y = ax + b \Rightarrow \{\begin{array}{l} 2 a + b = 0 \\ a + b = 1 \end{array} \Leftrightarrow \{\begin{cases} b = 2 \\ a = - 1 \end{cases} \Rightarrow d : y = - x + 2 \Rightarrow Thể tích của miền phẳng D giới hạn bởi \{\begin{cases} y = x; y = - x + 2 \\ x = 1; x = 2 \end{cases} khi quay D quanh trục Ox là V = π \int_{1}^{2} [x^{2} - {(2 - x)}^{2}] d x = 2 π$

Câu 25:

Một chiếc ô tô bắt đầu lăn bánh cho tới khi đạt vận tốc tối đa di chuyển được bao nhiêu mét?

Biết vận tốc ô tô được tính bởi công thức: V(t) = $3 t - \frac{3 t^{2}}{40} (m / s)$

A.200m

B.300m

C.400m

D.500m

Đáp án C.

$V (t) = 3 t - \frac{3 t^{2}}{40} \Rightarrow V' (t) = 3 - \frac{6}{40} t V' (t) = 0 \Leftrightarrow t = 20 \Rightarrow V_{\max} = V (20) = 30 (m / s) \Rightarrow S = \int_{0}^{20} (3 t - \frac{3 t^{2}}{40}) d t = 400 (m)$

Bắt đầu thi ngay

Bài thi liên quan