200 câu trắc nghiệm Phương pháp tọa độ trong không gian nâng cao (P1)
-
10285 lượt thi
-
25 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
 Xem đáp án
Xem đáp án
Chọn B
Gọi A (a; 0; 0), B(0; b; 0) và C(0; 0; c) với abc ≠ 0. Phương trình mặt phẳng (P) đi qua ba điểm A, B, C là
.
Vì M(1;2;3) ∈ (P) nên ta có: .
Điểm M là trực tâm của tam giác ABC.
Phương trình mặt phẳng (P) là: <=> x + 2y + 3z - 14 = 0
Câu 2:
Trong không gian Oxyz, cho ba điểm A(0;0;-1), B(-1;1;0), C(1;0;1). Tìm điểm M sao cho 3MA2 + 2MB2 - MC2 đạt giá trị nhỏ nhất.
 Xem đáp án
Xem đáp án
Chọn D
Cách 1: Giả sử
Cách 2: Ta có:
Câu 3:
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C (0;0;c), trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I (1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị lớn nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?
 Xem đáp án
Xem đáp án
Chọn C
Câu 4:
Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).
 Xem đáp án
Xem đáp án
Chọn C
Câu 5:
Trong không gian Oxyz, cho điểm H (2;1;1). Gọi (P) là mặt phẳng đi qua H và cắt các trục tọa độ tại A, B, C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là:
 Xem đáp án
Xem đáp án
Chọn A
Cách 1. Giả sử A (a; 0; 0) ∈ Ox, B (0;b;0) ∈ Oy, C (0;0;c) ∈ Oz.
Khi đó mặt phẳng (P) có dạng:
Do H là trực tâm tam giác ABC nên:
Vậy phương trình của mặt phẳng (P) là:
Cách 2. Vì tứ diện OABC có các cạnh đôi một vuông tại O và H là trực tâm tam giác ABC nên (tham khảo bài tập 4, trang 105 SGK HH11).
Suy ra Khi đó phương trình mặt phẳng (P) có dạng: 2x + y + x + D = 0
H ∈ (P) nên: 2.2 + 1 + 1 + D = 0 => D = -6
Vậy phương trình mặt phẳng là: 2x + y + z - 6 = 0
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (0; 0; -2), B(4; 0; 0). Mặt cầu (S) có bán kính nhỏ nhất, đi qua O, A, B có tâm là:
 Xem đáp án
Xem đáp án
Chọn C
Gọi J là trung điểm AB = > J = (2;0;-1)
Tam giác ABO vuông tại O nên J là tâm đường tròn ngoại tiếp tam giác OAB. Gọi I là tâm mặt cầu (S), (S) qua các điểm A, B, O. Ta có đường thẳng IJ qua J và có một VTCP là
nên có PTTS:
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho A (-3;0;0), B (0;0;3), C (0;-3;0) và mặt phẳng (P): x + y + z - 3 = 0. Tìm trên (P) điểm M sao cho nhỏ nhất.
 Xem đáp án
Xem đáp án
Chọn D
Câu 8:
Trong không gian với hệ tọa độ Oxyz cho điểm A (3;2;-1) và đường thẳng
Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.
 Xem đáp án
Xem đáp án
Chọn A
+ d qua M0 (0;0;1) có vectơ chỉ phương
+ Gọi H, K lần lượt là hình chiếu của A lên (P) và d. Ta có: d(A, (P)) = AH ≤ AK
Đẳng thức xảy ra khi và chỉ khi H ≡ K. Do đó d(A, (P))max = AK
Khi đó (P) đi M0 (0;0;1) nhận làm vectơ pháp tuyến.
Câu 9:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và
Mặt cầu có một đường kính là đoạn thẳng vuông góc chung của d1 và d2 có phương trình là:
 Xem đáp án
Xem đáp án
Chọn C
Vectơ chỉ phương của d1 và d2 lần lượt là
Gọi AB là đoạn vuông góc chung của d1 và d2 với A ∈ d1 và B ∈ d2
Suy ra: A (-1+2a; -1+a; -1+3a); B (2+b; 2b; 9+3b)
Khi đó: = (-2a + b + 3; -a + 2b + 1; -3a + 3b + 10)
Vì AB là đoạn vuông góc chung của d1 và d2 nên:
Gọi I là tâm mặt cầu (S) có đường kính là AB.
Suy ra
Vậy phương trình mặt cầu:
Câu 10:
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D.
 Xem đáp án
Xem đáp án
Chọn B
Gọi M là trung điểm BB'. Ta có: CK // A'M => CK // (A'MD)
Khi đó d(CK, A'D) = d (CK, (A'MD)). Gắn hệ trục tọa độ như hình vẽ:
Ta có: A(0;0;0), B(a;0;0), D(0;a;0), A'(0;0;a), B'(a;0;a), C(a;a;0), M(a;0;a/2).
Vậy mặt phẳng (A'MD) nhận làm vectơ pháp tuyến.
Phương trình (A'MD) là x + 2y + 2z - 2a = 0
Do đó:
Câu 11:
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5) và D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức đạt giá trị nhỏ nhất. Khi đó tọa độ của M là:
 Xem đáp án
Xem đáp án
Chọn D
Vậy M là hình chiếu vuông góc của G lên mặt phẳng (Oyz) nên M (0;1;4)
Câu 12:
Một khối đa diện được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ.
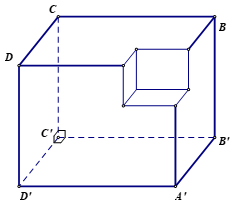
Gọi S là khối cầu có thể tích lớn nhất chứa trong H và tiếp xúc với các mặt phẳng (A'B'C'D'), (BCC'B') và (DCC'D'). Tính bán kính của S.
 Xem đáp án
Xem đáp án
Chọn B
Gọi M là đỉnh của hình lập phương có cạnh bằng 1 nằm trên đường chéo AC' và nằm trên khối còn lại sau khi cắt. Gọi I là tâm của khối cầu có thể tích lớn nhất thỏa yêu cầu bài toán.
Suy ra I thuộc đoạn thẳng C'M và mặt cầu tâm I cần tìm đi qua điểm M
Cách khác: Chọn hệ trục tọa độ Oxyz sao cho C'(0;0;0), B' (0;3;0), D'(3;0;0), C (0;0;3).
Khi đó M(2;2;2)
Ta có phương trình đường thẳng C'M là với 2 > 0 > t do I thuộc đoạn thẳng C'M
Câu 13:
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1; 2; 3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC
 Xem đáp án
Xem đáp án
Chọn B
Gọi A(a;0;0), B(0;b;0), C(0;0;c). Ta có phương trình mặt phẳng (P) là:
Gọi H là hình chiếu của O lên (P). Ta có: d(O, (P)) = OH ≤ OM
Do đó max d(O, (P)) = OM khi và chỉ khi (P) qua M nhận làm VTPT.
Do đó (P) có phương trình:
Câu 14:
Cho hình chóp S.ABCD có cạnh bằng bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có AB = 2a, AD = a. Gọi K là điểm thuộc BC sao cho . Tính khoảng cách giữa hai đường thẳng AD và SK.
 Xem đáp án
Xem đáp án
Chọn A
Gọi O là giao điểm của AC và BD, M là trung điểm của BC, N là trung điểm của CD.
Chọn hệ trục tọa độ Oxyz sao cho:
Câu 15:
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức AM2 + BM2 = 30 là một mặt cầu (S). Tọa độ tâm I và bán kính R của mặt cầu (S) là:
 Xem đáp án
Xem đáp án
Chọn C
Gọi tọa độ điểm M(x;y;z)
là phương trình của mặt cầu (S), có tâm I (-1;-1;-4) và bán kính R = 3
Câu 16:
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(1;0;0), B(0;1;0), C(0;0;1), D(0;0;0). Hỏi có bao nhiêu điểm cách đều 4 mặt phẳng (ABC), (CDA), (BCD), (DAB).
 Xem đáp án
Xem đáp án
Chọn D
Gọi điểm cần tìm là M (x0; y0; z0)
Phương trình mặt phẳng (ABC) là:
Phương trình mặt phẳng (BCD) là: x = 0
Phương trình mặt phẳng (CDA) là: y = 0
Phương trình mặt phẳng (DAB) là: z= 0.
Ta có M cách đều 4 mặt phẳng (ABC), (CDA), (BCD), (DAB) nên:
Ta có các trường hợp sau:
Vậy có 8 điểm M thỏa mãn bài toán.
Câu 17:
Trong không gian Oxyz, cho tứ diện S.ABC có S(0;0;1), A(1;0;1), B(0;1;1), C (0;0;2). Hỏi tứ diện S.ABC có bao nhiêu mặt phẳng đối xứng?
 Xem đáp án
Xem đáp án
Chọn D
Tức là tứ diện SABC có các cạnh SA, SB, SC bằng nhau và đôi một vuông góc.
Vậy tứ diện SABC có tất cả ba mặt phẳng đối xứng đó là:
Câu 18:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là: .
Cho ba điểm A, M, B nằm trên mặt cầu (S) sao cho góc AMB = . Diện tích tam giác AMB có giá trị lớn nhất bằng?
 Xem đáp án
Xem đáp án
Do đó diện tích tam giác AMB có giá trị lớn nhất bằng 4
Câu 19:
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(2;1;3), B(1;-1;2), C(3;-6;1). Điểm M(x;y;z) thuộc mặt phẳng (Oyz) sao cho MA2 + MB2 + MC2 đạt giá trị nhỏ nhất. Tính giá trị của biểu thức P = x+y+z
 Xem đáp án
Xem đáp án
Chọn A
Gọi G là trọng tâm tam giác ABC. Suy ra: G(2;-2;2)
Do tổng GA2 + GB2 + GC2 không đổi nên MA2 + MB2 + MC2 đạt giá trị nhỏ nhất khi và chỉ khi GM2 nhỏ nhất
Mà S nằm trên mặt phẳng (Oyz) nên M là hình chiếu vuông góc của G lên mặt phẳng (Oyz). Suy ra: M(0;-2;2)
Vậy P = x+y+z = 0 + (-2) + 2 = 0
Câu 20:
Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng?
 Xem đáp án
Xem đáp án
Chọn A
Theo giả thiết hình thang ABCD vuông tại A và B và có diện tích bằng 6√2 nên:
Do ABCD là hình thang vuông tại A và B nên . Giả sử , khi đó ta có:
Câu 21:
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Lấy điểm M thuộc đoạn AD', điểm N thuộc đoạn BD sao cho AM = DN = x, (0 < x < a√2/2). Tìm x theo a để đoạn MN ngắn nhất.
 Xem đáp án
Xem đáp án
Chọn A
Câu 22:
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(0;0;-6), B(0;1;-8), C(1;2;-5) và D(4;3;8). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó?
 Xem đáp án
Xem đáp án
Chọn C
Ta có , suy ra bốn điểm A, B, C, D không đồng phẳng. Gọi (P) là mặt phẳng cách đều bốn điểm A, B, C, D.
TH1: Có một điểm nằm khác phía với ba điểm còn lại so với (P). Có bốn mặt phẳng thỏa mãn.
TH2: Mỗi phía của mặt phẳng (P) có hai điểm. Có ba mặt phẳng thỏa mãn.
Vậy có bảy mặt phẳng thỏa mãn.
Câu 23:
Trong không gian Oxyz, cho ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng d. Phương trình tham số của đường thẳng d là:
 Xem đáp án
Xem đáp án
Ta thấy không cùng phương nên ba điểm A, B, C không thẳng hàng.
M cách đều hai điểm A, B nên điểm M nằm trên mặt trung trực của AB. M cách đều hai điểm B, C nên điểm M nằm trên mặt trung trực của B, C.
Do đó tập hợp tất cả các điểm m cách đều ba điểm A, B, C là giao tuyến của hai mặt trung trực của AB và BC.
Gọi (P), (Q) lần lượt là các mặt phẳng trung trực của AB và BC. K(0; 3/2; 1/2) là trung điểm AB; N(1/2; -1/2; 1) là trung điểm BC.
(P) đi qua K và nhận làm véctơ pháp tuyến nên (P):
hay (P): 2x - y + z + 1 = 0
(Q) đi qua N và nhận làm véctơ pháp tuyến nên (Q):
hay (Q): 3x - 5y +2z - 6 = 0
Ta có . Nên d có véctơ chỉ phương
Cho y = 0 ta sẽ tìm được x = -8, z = 15 nên (-8; 0; 15) ∈ d. Vậy .
Câu 24:
Trong không gian Oxyz, cho hai điểm A(-1;2;1), B(1;2;-3) và đường thẳng d: . Tìm vectơ chỉ phương của đường thẳng Δ đi qua điểm A và vuông góc với d đồng thời cách B một khoảng lớn nhất.
 Xem đáp án
Xem đáp án
Chọn A
Gọi H là hình chiếu vuông góc của B lên Δ, lúc đó d(B, Δ) = BH ≤ BA
Do đó d(B, Δ) lớn nhất khi H ≡ A
Câu 25:
Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
 Xem đáp án
Xem đáp án
Chọn D
Giả sử (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 (a2 + b2 + c2 - d > 0)
và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
(S) qua A và O nên
Suy ra 2 - 2a + 2c = 0 (2)
Lấy (1) nhân 2 rồi cộng vế theo vế với (2) ta suy ra b = 2. Từ đó, suy ra I (a; 2; a-1)
Chu vi tam giác OAI bằng 6 + √2 nên OI + OA + AI = 6 + √2
+ Với a = -1 => I(-1; 2; -2) => R = 3. Do đó:
+ Với a = 2 => I (2;2;1) => R = 3. Do đó:
