Trắc nghiệm Toán 12 Kết nối tri thức Bài 16. Công thức tính góc trong không gian có đáp án
Trắc nghiệm Toán 12 Kết nối tri thức Bài 16. Công thức tính góc trong không gian có đáp án
-
68 lượt thi
-
20 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Trong hệ tọa độ \[Oxyz\], góc giữa đường thẳng \[Ox\] và đường thẳng \[Oy\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Do trong hệ trục \[Oxyz\], các trục \[Ox,Oy,Oz\] đôi một vuông góc với nhau nên góc giữa đường thẳng \[Ox\] và đường thẳng \[Oy\] là \[90^\circ .\]
Câu 2:
Trong hệ tọa độ \[Oxyz\], góc giữa đường thẳng \[Ox\] và mặt phẳng \[\left( {Oxy} \right)\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[{\overrightarrow u _{Ox}} = \left( {1;0;0} \right)\], \[{\overrightarrow n _{\left( {Oxy} \right)}} = \left( {0;0;1} \right)\].
Suy ra \[\sin \left( {Ox,\left( {Oxy} \right)} \right) = \cos \left| {{{\overrightarrow u }_{Ox}},{{\overrightarrow n }_{\left( {Oxy} \right)}}} \right| = \frac{{\left| {1.0 + 0.0 + 0.1} \right|}}{{\sqrt {{1^2} + {0^2} + {0^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = 0.\]
Do đó, góc giữa đường thẳng \[Ox\] và mặt phẳng \[\left( {Oxy} \right)\] là \[0^\circ .\]
Câu 3:
Trong hệ tọa độ \[Oxyz\], cho hai đường thẳng \[{\Delta _1}\] và \[{\Delta _2}\] có vectơ chỉ phương lần lượt là \[\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right)\], \[\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\]. Khi đó, khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Câu 4:
Trong hệ tọa độ \[Oxyz\], cho đường thẳng \[\Delta :\frac{x}{2} = \frac{y}{{ - 1}} = \frac{z}{2}.\] Tính \[{\mathop{\rm co}\nolimits} \sin \] của góc giữa đường thẳng \[\Delta \] và trục \[Ox\].
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[{\overrightarrow u _\Delta } = \left( {2; - 1;2} \right)\] và \[{\overrightarrow u _{Ox}} = \left( {1;0;0} \right)\].
Suy ra \[\cos \left( {\Delta ,Ox} \right) = \cos \left| {\left( {\overrightarrow {{u_\Delta }} ,\overrightarrow {{u_{Ox}}} } \right)} \right| = \frac{{\left| {2.1 + \left( { - 1} \right).0 + 2.0} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}} .\sqrt {{1^2} + {0^2} + {0^2}} }} = \frac{2}{3}.\]
Câu 5:
Trong không gian \[Oxyz\], cho hai đường thẳng \[{\Delta _1}\] và \[{\Delta _2}\] có vectơ chỉ phương lần lượt là \[\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right)\], \[\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\]. Gọi \[\varphi \] là góc giữa hai đường thẳng \[{\Delta _1}\] và \[{\Delta _2}.\] Xét các khẳng định sau:
a) \[\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}.\]
b) \[\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}.\]
c) \[{\Delta _1} \bot {\Delta _2} \Leftrightarrow {a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2} = 0.\]
d) \[\sin \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}.\]
Số khẳng định đúng trong các khẳng định trên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có khẳng định a và c đúng.
Câu 6:
II. Thông hiểu
Cho hai đường thẳng \[{\Delta _1}:\frac{{x - 1}}{3} = \frac{y}{2} = \frac{{z + 1}}{1},{\rm{ }}{\Delta _2}:\frac{x}{{ - 1}} = \frac{{y - 2}}{2} = \frac{{z - 3}}{{ - 1}}\]. Góc giữa \[{\Delta _1}\] và \[{\Delta _2}\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[{\overrightarrow u _{{\Delta _1}}} = \left( {3;2;1} \right)\], \[{\overrightarrow u _{{\Delta _2}}} = \left( { - 1;2; - 1} \right)\].
Góc giữa hai đường thẳng là:
\[\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {{{\overrightarrow u }_{{\Delta _1}}},{{\overrightarrow u }_{{\Delta _2}}}} \right)} \right| = \frac{{\left| {3.\left( { - 1} \right) + 2.2 + 1.\left( { - 1} \right)} \right|}}{{\sqrt {{3^2} + {2^2} + {1^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 0.\]
Vậy góc giữa \[{\Delta _1}\] và \[{\Delta _2}\] là \[90^\circ .\]
Câu 7:
Tính góc tạo bởi đường thẳng \[d:\frac{{x - 2}}{1} = \frac{{y - 5}}{2} = \frac{{z + 1}}{{ - 1}}\] và mặt phẳng \[\left( \alpha \right):2x + y + z - 1 = 0.\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \[{\overrightarrow u _d} = \left( {1;2; - 1} \right)\], \[{\overrightarrow n _{\left( \alpha \right)}} = \left( {2;1;1} \right)\].
Suy ra \[\sin \left( {d,\left( \alpha \right)} \right) = \cos \left| {{{\overrightarrow u }_d},{{\overrightarrow n }_{\left( \alpha \right)}}} \right| = \frac{{\left| {1.2 + 2.1 + \left( { - 1} \right).1} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{2^2} + {1^2} + {1^2}} }} = \frac{3}{6} = \frac{1}{2}.\]
Góc tạo bởi đường thẳng và mặt phẳng đó là \[30^\circ .\]
Câu 8:
Trong hệ tọa độ \[Oxyz\], cho mặt phẳng \[\left( P \right):2x - y - z - 3 = 0\] và \[\left( Q \right):x - z - 2 = 0\]. Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \[{\overrightarrow n _{\left( P \right)}} = \left( {2; - 1; - 1} \right)\], \[{\overrightarrow n _{\left( Q \right)}} = \left( {1;0; - 1} \right)\].
Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] bằng
\[\cos \left( {\left( P \right),\left( Q \right)} \right) = \cos \left| {{{\overrightarrow u }_{\left( P \right)}},{{\overrightarrow n }_{\left( Q \right)}}} \right|\]
\[ = \frac{{\left| {1.2 + 0.\left( { - 1} \right) + \left( { - 1} \right).\left( { - 1} \right)} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {0^2} + {{\left( { - 1} \right)}^2}} }} = \frac{3}{{2\sqrt 3 }} = \frac{{\sqrt 3 }}{2}.\]
Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] bằng \[30^\circ .\]
Câu 9:
Trong hệ tọa độ \[Oxyz\], cho ba điểm \[M\left( {1;0;0} \right)\], \[N\left( {0;1;0} \right)\] và \[P\left( {0;0;1} \right)\]. Cosin của góc giữa hai mặt phẳng \[\left( {MNP} \right)\] và \[\left( {Oxy} \right)\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[\overrightarrow {MN} = \left( { - 1;1;0} \right),\overrightarrow {MP} = \left( { - 1;0;1} \right),\]\[{\overrightarrow n _{\left( {Oxy} \right)}} = \left( {0;0;1} \right)\].
Suy ra \[{\overrightarrow n _{\left( {MNP} \right)}} = \left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 1}\\1&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&1\\{ - 1}&0\end{array}} \right|} \right) = \left( {1;1;1} \right).\]
Suy ra \[\cos \left( {\left( {MNP} \right),\left( {Oxy} \right)} \right) = \left| {\cos \left( {{{\overrightarrow n }_{\left( {Oxy} \right)}},{{\overrightarrow n }_{\left( {MNP} \right)}}} \right)} \right| = \frac{1}{{\sqrt 3 }}.\]
Câu 10:
Hãy tìm giá trị thực của \[m\] để góc giữa hai đường thẳng \[d:\left\{ \begin{array}{l}x = 1 + t\\y = - \sqrt 2 t\\z = 1 + t\end{array} \right.,{\rm{ }}t \in \mathbb{R}\] và \[d':\left\{ \begin{array}{l}x = 1 + t'\\y = - \sqrt 2 t'\\z = 1 + mt'\end{array} \right.,{\rm{ }}t' \in \mathbb{R}\] bằng \[60^\circ .\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[{\overrightarrow u _d} = \left( {1; - \sqrt 2 ;1} \right),{\overrightarrow u _{d'}} = \left( {1; - \sqrt 2 ;m} \right)\].
Suy ra \[\cos \left( {d,d'} \right) = \left| {\cos \left( {{{\overrightarrow u }_d},{{\overrightarrow u }_{d'}}} \right)} \right| = \frac{{\left| {1 + 2 + m} \right|}}{{2.\sqrt {{m^2} + 3} }}\].
Theo đề, góc giữa hai đường thẳng là \[60^\circ \], do đó \[\frac{{\left| {1 + 2 + m} \right|}}{{2.\sqrt {{m^2} + 3} }} = \frac{1}{2}\]
Suy ra \[2\left| {m + 3} \right| = 2\sqrt {\left( {{m^2} + 3} \right)} \]
\[{\left( {m + 3} \right)^2} = \left( {{m^2} + 3} \right)\]
\[6m + 6 = 0\]
\[m = - 1.\]
Vậy \[m = - 1.\]
Câu 11:
Trong không gian \[Oxyz\], cho đường thẳng \[{d_1}:\left\{ \begin{array}{l}x = 1\\y = 2 - t\\z = 3 + 2t\end{array} \right.\] và \[{d_2}:\left\{ \begin{array}{l}x = 4 + t\\y = 1 + mt.\\z = 2 - t\end{array} \right.\] Tìm \[m\] để cosin góc giữa hai đường thẳng bằng \[\frac{{\sqrt 5 }}{5}.\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \[{\overrightarrow u _{{d_1}}} = \left( {0; - 1;2} \right),{\overrightarrow u _{{d_2}}} = \left( {1;m; - 1} \right).\]
Suy ra \[\cos \left( {{d_1},{d_2}} \right) = \left| {\cos \left( {{{\overrightarrow u }_{{d_1}}},{{\overrightarrow u }_{{d_2}}}} \right)} \right| = \frac{{\left| { - m - 2} \right|}}{{\sqrt 5 .\sqrt {{m^2} + 2} }}\].
Để góc giữa hai đường thẳng bằng \[\frac{{\sqrt 5 }}{5}\] thì
\[\frac{{\left| { - m - 2} \right|}}{{\sqrt 5 .\sqrt {{m^2} + 2} }} = \frac{{\sqrt 5 }}{5}\]
\[5\left| { - m - 2} \right| = 5\sqrt {{m^2} + 2} \]
\[{\left( {m + 2} \right)^2} = {m^2} + 2\]
\[{m^2} + 4m + 4 = {m^2} + 2\]
\[m = - \frac{1}{2}.\]
Câu 12:
Trong không gian \[Oxyz\], cho điểm \[A\left( {0;2;2} \right)\]. Góc giữa đường thẳng \[OA\] và trục \[Oy\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \[\overrightarrow {OA} = \left( {0;2;2} \right)\], \[{\overrightarrow u _{Oy}} = \left( {0;1;0} \right)\].
Suy ra \[\cos \left( {OA,Oy} \right) = \left| {\cos \left( {{{\overrightarrow u }_{OA}},{{\overrightarrow u }_{Oy}}} \right)} \right| = \frac{2}{{2\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\]
Vậy góc giữa đường thẳng \[OA\] và trục \[Oy\] bằng \[45^\circ .\]
Câu 13:
Trong không gian \[Oxyz\], hai đường thẳng \[{d_1}:\frac{{x - 2}}{1} = \frac{{y + 1}}{{\sqrt 2 }} = \frac{{z - 3}}{1}\] và \[{d_2}:\frac{{x + 5}}{1} = \frac{{y + 3}}{{\sqrt 2 }} = \frac{{z - 5}}{m}\] tạo với nhau góc \[60^\circ \], giá trị của tham số \[m\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[{\overrightarrow u _{{d_1}}} = \left( {1;\sqrt 2 ;1} \right),{\overrightarrow u _{{d_2}}} = \left( {1;\sqrt 2 ;m} \right)\].
Suy ra \[\cos \left( {{d_1},{d_2}} \right) = \left| {\cos \left( {{{\overrightarrow u }_{{d_1}}},{{\overrightarrow u }_{{d_2}}}} \right)} \right| = \frac{{\left| {3 + m} \right|}}{{2.\sqrt {{m^2} + 3} }}\].
Để góc giữa hai đường thẳng bằng \[60^\circ \] thì \[\frac{{\left| {3 + m} \right|}}{{2.\sqrt {{m^2} + 3} }} = \cos 60^\circ \]
\[ \Leftrightarrow \frac{{\left| {3 + m} \right|}}{{2.\sqrt {{m^2} + 3} }} = \frac{1}{2}\]
\[ \Leftrightarrow 2\left| {3 + m} \right| = 2\sqrt {{m^2} + 3} \]
\[ \Leftrightarrow {\left( {m + 3} \right)^2} = \left( {\sqrt {{m^2} + 3} } \right)\]
\[ \Leftrightarrow {m^2} + 6m + 9 = {m^2} + 3\]
\[ \Leftrightarrow 6m + 6 = 0\]
\[ \Leftrightarrow m = - 1.\]
Câu 14:
Trong không gian \[Oxyz\], cho mặt phẳng \[\left( P \right):x - y + 2z + 1 = 0\]và đường thẳng \[d:\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z + 1}}{{ - 1}}\]. Xét các mệnh đề sau:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \[{\overrightarrow n _{\left( P \right)}} = \left( {1; - 1;2} \right),{\overrightarrow u _d} = \left( {1;2; - 1} \right)\].
Có \[\sin \left( {d,\left( P \right)} \right) = \cos \left| {{{\overrightarrow u }_d},{{\overrightarrow n }_{\left( P \right)}}} \right| = \frac{{\left| {1.1 + \left( { - 1} \right).2 + \left( { - 1} \right).2} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{2^2} + {1^2} + {{\left( { - 1} \right)}^2}} }} = \frac{3}{6} = \frac{1}{2}.\]
Suy ra \[\left( {d;\left( P \right)} \right) = 30^\circ .\]
Câu 15:
Tính góc \[\alpha \] giữa hai đường thẳng \[d:\left\{ \begin{array}{l}x = 2 + t\\y = - 1 + t\\z = 3\end{array} \right.\] và \[d':\left\{ \begin{array}{l}x = 1 - t'\\y = 2\\z = - 2 + t'.\end{array} \right.\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[{\overrightarrow u _d} = \left( {1;1;0} \right),{\overrightarrow u _{d'}} = \left( { - 1;0;1} \right)\].
Có \[\cos \left( {d,d'} \right) = \left| {\cos \left( {{{\overrightarrow u }_d},{{\overrightarrow u }_{d'}}} \right)} \right| = \frac{{\left| { - 1} \right|}}{2} = \frac{1}{2}.\]
Suy ra \[\alpha = 60^\circ .\]
Câu 16:
III. Vận dụng
Trong không gian \[Oxyz\], cho mặt phẳng \[\left( P \right):3x + 4y + 5z + 2 = 0\] và đường thẳng \[d\] là giao tuyến của hai mặt phẳng \[\left( \alpha \right):x - 2y + 1 = 0\] và \[\left( \beta \right):x - 2y - 3z = 0\]. Hãy tính số đo góc \[\alpha \] giữa \[d\] và \[\left( P \right)\].
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì \[d\] là giao tuyến của hai mặt phẳng \[\left( \alpha \right)\] và \[\left( \beta \right)\] nên \[{\overrightarrow u _d} = \left[ {{{\overrightarrow n }_{\left( \alpha \right)}},{{\overrightarrow n }_{\left( \beta \right)}}} \right]\].
Ta có: \[{\overrightarrow n _{\left( \alpha \right)}} = \left( {1; - 2;0} \right),{\overrightarrow n _{\left( \beta \right)}} = \left( {1; - 2; - 3} \right)\]
Suy ra \[{\overrightarrow u _d} = \left[ {{{\overrightarrow n }_{\left( \alpha \right)}},{{\overrightarrow n }_{\left( \beta \right)}}} \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 2}&0\\{ - 2}&{ - 3}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&1\\{ - 3}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&{ - 2}\\{ - 2}&{ - 2}\end{array}} \right|} \right) = \left( {6;3; - 6} \right) = 3\left( {2;1; - 2} \right).\]
Lấy \[{\overrightarrow u _d} = \left( {2;1; - 2} \right)\], \[{\overrightarrow n _{\left( P \right)}} = \left( {3;4;5} \right)\].
Ta có: \[\sin \left( {d,\left( P \right)} \right) = \cos \left| {{{\overrightarrow u }_d},{{\overrightarrow n }_{\left( P \right)}}} \right| = \frac{{\left| {2.3 + 1.4 + \left( { - 2} \right).5} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{3^2} + {4^2} + {5^2}} }} = 0.\]
Vậy số đo góc \[\alpha \] giữa \[d\] và \[\left( P \right)\] là \[90^\circ .\]
Câu 17:
Tìm tất cả các mặt phẳng \[\left( \alpha \right)\] chứa đường thẳng \[d:\frac{x}{1} = \frac{y}{{ - 1}} = \frac{z}{{ - 3}}\] và tạo với mặt phẳng \[\left( P \right):2x - z + 1 = 0\] góc \[45^\circ .\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Giả sử mặt phẳng \[\left( \alpha \right):Ax + By + Cz + D = 0\] với \[{A^2} + {B^2} + {C^2} \ne 0\].
Đường thẳng \[d\] đi qua \[O\left( {0;0;0} \right)\] có vectơ chỉ phương \[{\overrightarrow u _d} = \left( {1; - 1; - 3} \right)\].
Mặt phẳng \[\left( \alpha \right)\] chứa đường thẳng \[d\] nên \[{\overrightarrow u _d}.{\overrightarrow n _{\left( \alpha \right)}} = 0\].
Suy ra \[A - B - 3C = 0\].
Mà mặt phẳng \[\left( \alpha \right)\] tạo với \[\left( P \right)\] góc \[45^\circ \] nên
\[\cos \left( {\left( \alpha \right),\left( P \right)} \right) = \frac{{\left| {2A - C} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt 5 }} = \frac{{\sqrt 2 }}{2}\]
\[ \Leftrightarrow 2\left| {2A - C} \right| = \sqrt {10\left( {{A^2} + {B^2} + {C^2}} \right)} \]
\[ \Leftrightarrow 4{\left( {2A - C} \right)^2} = 10\left( {{A^2} + {B^2} + {C^2}} \right)\]
\[ \Leftrightarrow 16{A^2} - 16AC + 4{C^2} = 10\left( {{A^2} + {B^2} + {C^2}} \right)\] (1)
Thay \[A = B + 3C\] vào (1), được
\[ \Leftrightarrow 3{A^2} - 8AC - 3{C^2} = 5{B^2}\]
\[ \Leftrightarrow 3{\left( {B + 3C} \right)^2} - 8\left( {B + 3C} \right)C - 3{C^2} - 5{B^2} = 0\]
\[ \Leftrightarrow - 2{B^2} + 10BC = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}B = 5C\\B = 0\end{array} \right.\].
Với \[B = 0 \Rightarrow A = 3C \Rightarrow \left( \alpha \right):x + 3z = 0.\]
Với \[B = 5C\], chọn \[C = 1 \Rightarrow C = 5,A = 8\] nên \[\left( \alpha \right):8x + 5y + z = 0.\]
Câu 18:
Trong không gian \[Oxyz\], cho hai mặt phẳng \[\left( P \right):x - y - 6 = 0\] và \[\left( Q \right)\]. Biết rằng điểm \[H\left( {2; - 1; - 2} \right)\] là hình chiếu vuông góc của gốc tọa độ \[O\left( {0;0;0} \right)\] xuống mặt phẳng \[\left( Q \right)\]. Số đo góc giữa hai mặt phẳng \[\left( P \right)\] và mặt phẳng \[\left( Q \right)\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \[\overrightarrow {OH} = \left( {2; - 1; - 2} \right)\] là một vectơ pháp tuyến của mặt phẳng \[\left( Q \right)\].
Mặt phẳng \[\left( P \right)\] có \[{\overrightarrow n _{\left( P \right)}} = \left( {1; - 1;0} \right)\].
Ta có: \[\left| {\cos \left( {{{\overrightarrow n }_{\left( P \right)}},\overrightarrow {OH} } \right)} \right| = \frac{{\left| {2.1 + \left( { - 1} \right).\left( { - 1} \right) + 0.0} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} .\sqrt {{1^2} + {{\left( { - 1} \right)}^2} + {0^2}} }} = \frac{3}{{3\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\]
Vậy góc giữa hai mặt phẳng \[\left( P \right)\] và mặt phẳng \[\left( Q \right)\] bằng \[45^\circ .\]
Câu 19:
Trong không gian \[Oxyz\], cho hình chóp \[S.ABC\] có ba điểm \[S\left( {0;0;3} \right)\], \[A\left( {0;0;0} \right)\], \[B\left( {1;0;0} \right)\], \[C\left( {0;2;0} \right)\] và mặt phẳng \[\left( P \right):x + y + z - 3 = 0\]. Xét các mệnh đề sau:
a) Cosin góc giữa hai mặt phẳng \[\left( {SAB} \right)\] và mặt phẳng \[\left( {ABC} \right)\] bằng \[0.\]
b) Cosin góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và mặt phẳng \[\left( {ABC} \right)\] bằng \[\frac{2}{7}.\]
c) Cosin góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và mặt phẳng \[\left( P \right)\] bằng \[\frac{{10\sqrt 3 }}{{21}}.\]
d) Góc giữa hai mặt phẳng \[\left( {SAC} \right)\] và mặt phẳng \[\left( {ABC} \right)\] bằng \[90^\circ .\]
Số mệnh đề đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \[\overrightarrow {SA} = \left( {0;0; - 3} \right),\overrightarrow {SB} = \left( {1;0; - 3} \right),\overrightarrow {SC} = \left( {0;2; - 3} \right)\], \[\overrightarrow {AB} = \left( {1;0;0} \right)\], \[\overrightarrow {AC} = \left( {0;2;0} \right)\].
Suy ra \[{\overrightarrow n _{\left( {SAB} \right)}} = \left[ {\overrightarrow {SA} ,\overrightarrow {SB} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 3}\\0&{ - 3}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 3}&0\\{ - 3}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&0\\1&0\end{array}} \right|} \right) = \left( {0; - 3;0} \right).\]
\[{\overrightarrow n _{\left( {SBC} \right)}} = \left[ {\overrightarrow {SB} ,\overrightarrow {SC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 3}\\2&{ - 3}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 3}&1\\{ - 3}&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&0\\0&2\end{array}} \right|} \right) = \left( {6;3;2} \right).\]
\[{\overrightarrow n _{\left( {ABC} \right)}} = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&0\\2&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&1\\0&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&0\\0&2\end{array}} \right|} \right) = \left( {0;0;2} \right).\]
\[{\overrightarrow n _{\left( {SAC} \right)}} = \left[ {\overrightarrow {SA} ,\overrightarrow {SC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - 3}\\2&{ - 3}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 3}&0\\{ - 3}&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&0\\0&2\end{array}} \right|} \right) = \left( { - 6;0;0} \right).\]
a) Cosin góc giữa hai mặt phẳng \[\left( {SAB} \right)\] và mặt phẳng \[\left( {ABC} \right)\] bằng
\[\cos \left( {\left( {SAB} \right),\left( {ABC} \right)} \right) = \cos \left( {{{\overrightarrow n }_{\left( {SAB} \right)}},{{\overrightarrow n }_{\left( {ABC} \right)}}} \right) = 0.\]
Do đó, ý a đúng.
b) Cosin góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và mặt phẳng \[\left( {ABC} \right)\] bằng
\[\cos \left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \cos \left( {{{\overrightarrow n }_{\left( {SBC} \right)}},{{\overrightarrow n }_{\left( {ABC} \right)}}} \right) = \frac{{\left| {6.0 + 3.0 + 2.2} \right|}}{{\sqrt {{6^2} + {3^2} + {2^2}} .\sqrt {{0^2} + {0^2} + {2^2}} }} = \frac{2}{7}.\]
Do đó, ý b đúng.
c) Ta có: \[{\overrightarrow n _{\left( P \right)}} = \left( {1;1;1} \right)\].
Cosin góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và mặt phẳng \[\left( P \right)\] bằng
\[\cos \left( {\left( {SBC} \right),\left( P \right)} \right) = \cos \left( {{{\overrightarrow n }_{\left( {SBC} \right)}},{{\overrightarrow n }_{\left( P \right)}}} \right) = \frac{{\left| {6.1 + 3.1 + 2.1} \right|}}{{\sqrt {{6^2} + {3^2} + {2^2}} .\sqrt {{1^2} + {1^2} + {1^2}} }} = \frac{{11\sqrt 3 }}{{21}}.\]
Do đó, ý c sai.
d) Ta có:
\[\cos \left( {\left( {SAC} \right),\left( {ABC} \right)} \right) = \cos \left( {{{\overrightarrow n }_{\left( {SAC} \right)}},{{\overrightarrow n }_{\left( {ABC} \right)}}} \right) = \frac{{\left| { - 6.0 + 0.0 + 0.2} \right|}}{{\sqrt {{{\left( { - 6} \right)}^2} + {0^2} + {0^2}} .\sqrt {{0^2} + {0^2} + {2^2}} }} = 0.\]
Vậy góc giữa hai mặt phẳng \[\left( {SAC} \right)\] và mặt phẳng \[\left( {ABC} \right)\] bằng \[90^\circ .\]
Vậy ý d đúng.
Vậy có 3 mệnh đề đúng.
Câu 20:
Trong không gian \[Oxyz\] cho hình chóp \[S.ABCD\] có \[S\left( {0;0;\frac{{a\sqrt 3 }}{2}} \right),\]\[A\left( {\frac{a}{2};0;0} \right),\]\[B\left( { - \frac{a}{2};0;0} \right)\], \[C\left( { - \frac{a}{2};a;0} \right)\],\[D\left( {\frac{a}{2};a;0} \right)\] với \[a > 0\]. Tính góc giữa đường thẳng \[SD\] và mặt phẳng \[\left( {SAC} \right)\]. (Kết quả làm tròn đến hàng đơn vị của độ).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
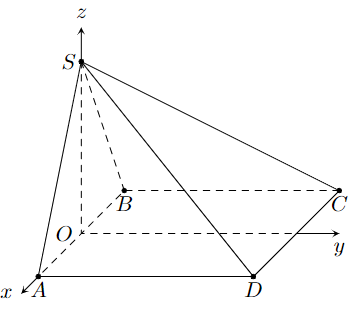
Ta có: \[\overrightarrow {SD} = \left( {\frac{a}{2};a; - \frac{{a\sqrt 3 }}{2}} \right) = a\left( {\frac{1}{2};1; - \frac{{\sqrt 3 }}{2}} \right)\],
\[\overrightarrow {SA} = \left( {\frac{a}{2};0; - \frac{{a\sqrt 3 }}{2}} \right) = a\left( {\frac{1}{2};0; - \frac{{\sqrt 3 }}{2}} \right)\],
\[\overrightarrow {SC} = \left( { - \frac{a}{2};a; - \frac{{a\sqrt 3 }}{2}} \right) = a\left( { - \frac{1}{2};1; - \frac{{\sqrt 3 }}{2}} \right)\].
Vectơ pháp tuyến của mặt phẳng \[\left( {SAC} \right)\] là \[\overrightarrow n = \left[ {\overrightarrow {SA} ,\overrightarrow {SC} } \right]\].
Ta có: \[\overrightarrow n = \left[ {\overrightarrow {SA} ,\overrightarrow {SC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - \frac{{\sqrt 3 }}{2}}\\1&{ - \frac{{\sqrt 3 }}{2}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - \frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}\\{ - \frac{{\sqrt 3 }}{2}}&{ - \frac{1}{2}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\frac{1}{2}}&0\\{ - \frac{1}{2}}&1\end{array}} \right|} \right) = \left( {\frac{{\sqrt 3 }}{2};\frac{{\sqrt 3 }}{2};\frac{1}{2}} \right).\]
Ta có: \[\sin \left( {SD,\left( {SAC} \right)} \right) = \left| {\cos \left( {\overrightarrow {SD} ,{{\overrightarrow n }_{\left( {SAC} \right)}}} \right)} \right|\]
\[ = \frac{{\left| {\frac{{\sqrt 3 }}{2}.\frac{1}{2} + 1.\frac{{\sqrt 3 }}{2} + \left( { - \frac{{\sqrt 3 }}{2}} \right).\frac{1}{2}} \right|}}{{\sqrt {{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2}} .\sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {1^2} + {{\left( { - \frac{{\sqrt 3 }}{2}} \right)}^2}} }}\]
\[ = \frac{{\sqrt {42} }}{{14}}.\]
Suy ra \[\widehat {\left( {SD,\left( {SAC} \right)} \right)} \approx 28^\circ .\]
