Chuyên đề Toán 12 Bài 2: Các phép toán trên tập hợp số phức có đáp án
-
1296 lượt thi
-
34 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 7:
 Xem đáp án
Xem đáp án
Ta có:
Suy ra, có phần thực bằng 6 và phần ảo bằng 8.
Do đó tổng phần thực và phần ảo của bằng 14.
Câu 8:
 Xem đáp án
Xem đáp án
Chọn C.
Ta có:
là số thực khi và chỉ khi
Câu 10:
 Xem đáp án
Xem đáp án
Chọn C.
Ta có:
Do đó
Câu 12:
Gọi lần lượt có điểm biểu diễn là M và N trên mặt phẳng Oxy ở hình bên. Khi đó bằng
 Xem đáp án
Xem đáp án
Chọn C.
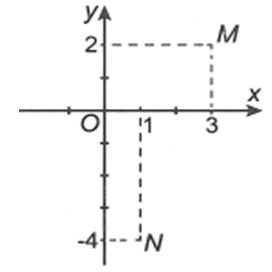
Từ hình vẽ ta có điểm M(3;2) biểu diễn số phức
điểm N(1;-4) biểu diễn số phức
Ta có
Câu 13:
Cho số phức z = a + bi, với a, b là các số thực thỏa mãn a + bi + 2i(a - bi) + 4 = i, với i là đơn vị ảo. Môđun của là
 Xem đáp án
Xem đáp án
Chọn A.
Ta có Suy ra
Do đó VậyCâu 15:
Cho là các số phức thỏa mãn và Giá trị của biểu thức là
 Xem đáp án
Xem đáp án
Đặt
Suy ra và
Ta có:
Suy raCâu 17:
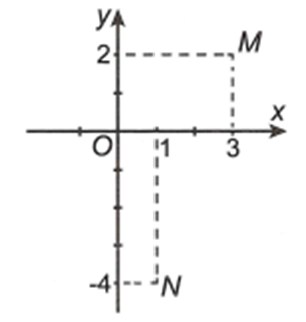
 Xem đáp án
Xem đáp án
Dựa vào hình vẽ ta có được
Câu 18:
 Xem đáp án
Xem đáp án
Chọn A.
Ta có:
Suy ra điểm biểu diễn cho số phức z là M(4,-7)Câu 19:
 Xem đáp án
Xem đáp án
Chọn C
Ta có
A là điểm biểu diễn của số phức 4 - 3i nên A(4;-3)
B là điểm biểu diễn của số phức (1 + 2i)i nên B(-2;1)
C là điểm biểu diễn của số phức nên C(0;-1)
Điều kiện để ABCD là hình bình hành là
Câu 20:
 Xem đáp án
Xem đáp án
Chọn D
Ta có: A(2;-1), B(-1;6), C(8;1)
Gọi G là trọng tâm tam giác ABC
Câu 21:
Cho các số phức thoả mãn . Gọi A, B lần lượt là các điểm biểu diễn số phức trên mặt phẳng toạ độ. Diện tích S của (với O là gốc toạ độ) là
 Xem đáp án
Xem đáp án
Chọn B.
Ta có: ,
vuông tại O (vì )
Câu 22:
 Xem đáp án
Xem đáp án
Chọn A
Đặt
Ta có hệ phương trình:
Do đó z = 1 + i nên có một số phức thỏa mãn.
Câu 23:
 Xem đáp án
Xem đáp án
Chọn C.
Ta có:
Suy ra điểm M biểu diễn số phức z là giao của hai đường tròn và
Vì ( là tâm của các đường tròn ) nên và tiếp xúc nhau).
Suy ra: Có một số phức thỏa mãn yêu cầu.
Câu 24:
 Xem đáp án
Xem đáp án
Chọn B
Nhận xét: Từ giả thiết, ứng với mỗi cho ta duy nhất một số phức z
Đặt , khi đó ta có
Hàm số có bảng biến thiên:
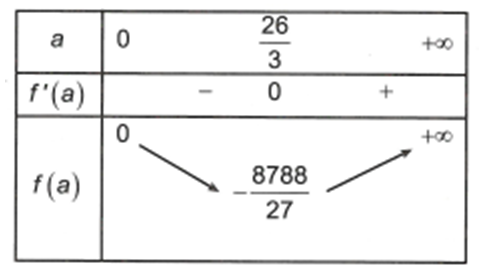
Đường thẳng y = -4 cắt đồ thị hàm số f(a) tại hai điểm nên phương trình có hai nghiệm khác 1 (do ). Thay giá trị môđun của z vào giả thiết ta được 3 số phức thỏa mãn điều kiện.
Câu 25:
Có tất cả bao nhiêu giá trị nguyên của m để có đúng hai số phức z thỏa mãn và
 Xem đáp án
Xem đáp án
Chọn B
Giả sử và M(x;y) là điểm biểu diễn số phức z
Ta có:
Khi đó điểm biểu diễn số phức z nằm trên đường tròn (C) có tâm I(2m - 1;1) bán kính R = 10
Lại có
Khi đó điểm biểu diễn số phức z cũng nằm trên đường thẳng
Có đúng hai số phức z thỏa mãn nếu đường thẳng cắt đường tròn (C) tại 2 điểm phân biệt.
Tức là
Vậy có 41 giá trị nguyên của m để có đúng hai số phức z thỏa mãn yêu cầu bài toán.
Câu 26:
 Xem đáp án
Xem đáp án
Chọn B
Đặt
Ta có:
Lại có:
Suy ra
Mà
Vậy có hai số phức z thỏa mãn.
Câu 27:
 Xem đáp án
Xem đáp án
Chọn A
Dễ thấy m > 0
Đặt ta có hệ phương trình.
Phương trình là đường tròn tâm O, bán kính R = 1
Phương trình là đường tròn tâm bán kính R = m.
Có duy nhất số phức thỏa mãn đề bài
<=> Hệ phương trình có nghiệm duy nhất
<=> Hai đường tròn này tiếp túc với nhau
(thỏa mãn m > 0).
Vậy, có hai số thực thỏa mãn.
Câu 28:
 Xem đáp án
Xem đáp án
Chọn D
Đặt Ta có
Ta có hệ: hoặc
hoặc
Suy ra
Vậy có 8 cặp số (a;b) do đó có 8 số phức thỏa mãn.
Câu 29:
 Xem đáp án
Xem đáp án
Chọn B.
Đặt
Vì là số thực nên
Tập hợp tất cả các điểm biểu diễn của z là đường tròn có tâm I(3;-4) bán kính R = 5
Vậy a + b + R = 4
Câu 30:
 Xem đáp án
Xem đáp án
Chọn C
Gọi thì
Gọi M là điểm biểu diễn số phức z và các điểm Dễ thấy
Khi đó:
Vậy tập hợp các điểm M biểu diễn số phức z là elip có hai tiêu điểm , độ dài trục lớn là 2a = 10
Câu 31:
Cho số phức z thỏa mãn và Tập hợp các điểm biểu diễn số phức w là đường tròn có tâm là
 Xem đáp án
Xem đáp án
Chọn A
Ta có
Vậy tập hợp các điểm biểu diễn số phức w là đường tròn (C) có tâm I(-3;-4)
Câu 32:
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu biễn các số phức z thỏa mãn là đường thẳng có phương trình
 Xem đáp án
Xem đáp án
Chọn C
Đặt
Gọi M(x;y) là điểm biểu diễn của số phức z
Ta có:
Vậy tập hợp các điểm biểu biễn các số phức z thỏa mãn yêu cầu bài toán là đường thẳng có phương trình là x - 2y = 0
Câu 33:
Gọi M là điểm biểu diễn số phức z thỏa mãn Tập hợp tất cả các điểm M như vậy là
 Xem đáp án
Xem đáp án
Chọn A
Gọi M(x;y) là điểm biểu diễn số phức
Khi đó
Vậy tập hợp tất cả các điểm M là một đường parabol.
Câu 34:
 Xem đáp án
Xem đáp án
Gọi M(a;b) là điểm biểu diễn của số phức z và A(-1;3) là điểm biểu diễn số phức -1 + 3i
Khi đó
Suy ra Tập hợp các điểm biểu diễn của z là hình vành khăn giới hạn bởi hai đường tròn (A;3) và (A;5), kể cả các điểm nằm trên hai đường tròn này.
