Trắc nghiệm Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số có đáp án (Mới nhất)
Trắc nghiệm Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số có đáp án (Mới nhất)
-
1275 lượt thi
-
65 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
Cho hàm số xác định trên , với bất kỳ thuộc . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
A sai. Sửa lại cho đúng là .
B sai: Sửa lại cho đúng là .
C sai: Sửa lại cho đúng là .
D đúng (theo định nghĩa). Chọn D.
Câu 3:
 Xem đáp án
Xem đáp án
A sai: Sửa lại cho đúng là .
B sai: Sửa lại cho đúng là .
C đúng (theo dáng điệu của đồ thị hàm đồng biến). Chọn C.
D sai (đối nghĩa với đáp án C).
Câu 4:
Cho hàm số có đạo hàm trên .Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Chọn C. Sửa lại cho đúng là Nếu hàm số đồng biến trên thì
Câu 5:
 Xem đáp án
Xem đáp án
A sai: Vì tổng của hàm đồng biến với hàm nghịch biến không kết luận được điều gì.
B sai: Để cho khẳng định đúng thì đồng biến trên .
C sai: Hàm số , phải là các hàm dương trên mới thoả mãn.
D đúng. Chọn D.
Câu 6:
Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Ví dụ hàm số đồng biến trên , trong khi đó hàm số nghịch biến trên và . Do đó B sai. Chọn B.
Câu 7:
Nếu hàm số đồng biến trên khoảng thì hàm số đồng biến trên khoảng nào trong các khoảng sau đây?
 Xem đáp án
Xem đáp án
Câu 8:
Nếu hàm số đồng biến trên khoảng thì hàm số đồng biến trên khoảng nào?
 Xem đáp án
Xem đáp án
Tổng quát: Hàm số liên tục và đồng biến trên khoảng thì hàm số liên tục và đồng biến trên khoảng . Chọn C.
Cách trắc nghiệm nhanh. Ta ốp
Câu 10:
 Xem đáp án
Xem đáp án
Đạo hàm: và .
Suy ra hàm số đã cho luôn đồng biến trên R. Chọn A.
Câu 11:
Hàm số nghịch biến trên khoảng nào được cho dưới đây?
 Xem đáp án
Xem đáp án
Ta có:
Ta có .
Vậy hàm số đã cho nghịch biến trên khoảng . Chọn A.
Câu 12:
Hàm số nào sau đây nghịch biến trên toàn trục số?
 Xem đáp án
Xem đáp án
Để hàm số nghịch biến trên toàn trục số thì hệ số của phải âm. Do đó A & D không thỏa mãn.
Xét B: Ta có và .
Suy ra hàm số này luôn nghịch biến trên R. Chọn B.
Câu 14:
Cho hàm số . Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Ta có
Vẽ phác họa bảng biến thiên và kết luận được rằng hàm số
● Đồng biến trên các khoảng và .
● Nghịch biến trên các khoảng và . Chọn B.
Câu 15:
 Xem đáp án
Xem đáp án
Hàm trùng phương không thể nghịch biến trên R. Do đó ta loại C & D.
Để hàm số nghịch biến trên R số thì hệ số của phải âm. Do đó loại A.
Vậy chỉ còn lại đáp án B. Chọn B.
Thật vậy: Với có .
Câu 16:
Các khoảng nghịch biến của hàm số là:
 Xem đáp án
Xem đáp án
Tập xác định: . Đạo hàm:
Vậy hàm số nghịch biến trên các khoảng và . Chọn C.
Chú ý: Sai lầm hay gặp là chọn A hoặc B. Lưu ý rằng hàm bậc nhất trên nhất này là đồng biến trên từng khoảng xác định.
Câu 17:
Cho hàm số . Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Tập xác định: . Đạo hàm: .
Vậy hàm số nghịch biến trên các khoảng và . Chọn DCâu 18:
Cho hàm số . Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Tập xác định: Đạo hàm
Vậy hàm số đồng biến trên các khoảng và
Suy ra hàm số đồng biến trên Chọn D.
Bình luận: Hàm số đồng biến trên tất cả các khoảng con của các khoảng đồng biến của hàm số. Cụ thể trong bài toán trên:
= Hàm số đồng biến trên ;
= .
Suy ra hàm số đồng biến trên
Câu 19:
 Xem đáp án
Xem đáp án
Ta có
A. B.
C. D.
Chọn B.
Câu 20:
Cho hàm số . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Tập xác định . Đạo hàm .
Vẽ bảng biến thiên, suy ra được hàm số nghịch biến trên . Chọn C.
Câu 21:
 Xem đáp án
Xem đáp án
Tập xác định . Đạo hàm
Vẽ bảng biến thiên, suy ra được hàm số nghịch biến trên khoảng . Chọn C.
Câu 22:
Cho hàm số . Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Tập xác định: Đạo hàm
Xét phương trình
Vẽ bảng biến thiên, suy ra được hàm số nghịch biến trên khoảng Chọn C.
Câu 23:
Hàm số nào sau đây đồng biến trên ?
 Xem đáp án
Xem đáp án
Chọn B. Vì và .
Phương trình có vô số nghiệm nhưng các nghiệm tách rời nhau nên hàm số đồng biến trên R
Câu 24:
Hàm số nào sau đây đồng biến trên R?
 Xem đáp án
Xem đáp án
Xét hàm số
Ta có hàm số đồng biến trên
Chọn B.
Câu 25:
Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Xét hàm số . Ta có .
Suy ra hàm số nghịch biến trên và . Chọn C.
Câu 26:
Cho hàm số liên tục trên và có bảng biến thiên như sau:
Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?
I. Hàm số đã cho đồng biến trên các khoảng và .
II. Hàm số đã cho đồng biến trên khoảng .
III. Hàm số đã cho nghịch biến trên khoảng .
IV. Hàm số đã cho đồng biến trên khoảng .
 Xem đáp án
Xem đáp án
Nhìn vào bảng biến thiên ta thấy đồ thị hàm số đã cho đồng biến trên khoảng ; nghịch biến trên khoảng .
Suy ra II. Sai; III. Đúng; IV. Đúng.
Ta thấy khoảng chứa khoảng nên I Đúng.
Vậy chỉ có II sai. Chọn A.
Câu 27:
 Xem đáp án
Xem đáp án
Vì , mà hàm số đồng biến trên khoảng nên suy ra C đúng. Chọn C.
Câu 28:
Cho hàm số có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên ta thấy hàm số
● Đồng biến trên các khoảng và .
● Nghịch biến trên khoảng . Chọn C.
Câu 29:
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta có nhận xét sau
Hàm số nghịch biến trên khoảng và A sai (sai chỗ dấu ).
Hàm số có giá trị cực đại B sai.
Hàm số đồng biến khoảng và C đúng.
Hàm số có điểm cực tiểu là D sai.
Chọn C.
Câu 30:
Cho hàm số xác định, liên tục trên và có đồ thị như hình vẽ bên. Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Dựa vào đồ thị ta có kết quả: Hàm số đồng biến trên và , nghịch biến trên nên các khẳng định A, B, C đúng.
Theo định nghĩa hàm số đồng biến trên khoảng thì khẳng định D sai.
Ví dụ: Ta lấy nhưng
Chọn D.
Câu 31:
Cho hàm số liên tục trên và có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?
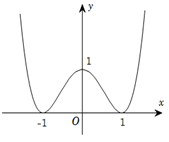
 Xem đáp án
Xem đáp án
Câu 32:
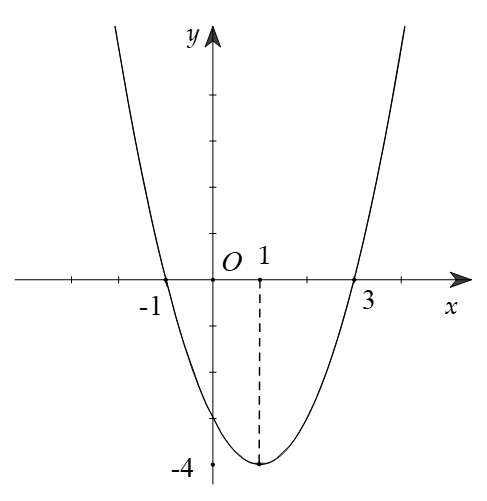
 Xem đáp án
Xem đáp án
Dựa vào đồ thị của hàm số , ta có nhận xét:
đổi dấu từ "+" sang "-" khi qua điểm x=-1
đổi dấu từ "-" sang "+" khi qua điểm x=3
Do đó ta có bảng biến thiên
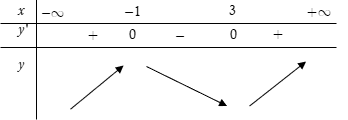
Dựa vào bảng biến thiên ta thấy B đúng. Chọn B.
Câu 33:
Cho hàm số và hai số thực a,b sao cho a<b Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Tập xác định:
Đạo hàm
Suy ra đồng biến trên . Do đó . Chọn C.
Câu 34:
Cho hàm số và hai số thực sao cho u>v
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Tập xác định:
Đạo hàm
Vẽ bảng biến thiên ta thấy được hàm số nghịch biến trên .
Do đó với thỏa mãn . Chọn C.
Câu 35:
Cho hàm số có đạo hàm trên sao cho Biết . Hỏi mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Từ giải thiết suy ra hàm số đồng biến trên khoảng . Do đó
Vậy A đúng. Chọn A.
Vậy B sai.
Tương tự cho các đáp án C và D.
Câu 36:
Hàm số đồng biến trên R khi:
 Xem đáp án
Xem đáp án
Quan sát các đáp án, ta sẽ xét hai trường hợp là: và
Nếu thì là hàm bậc nhất => để y đồng biến trên R khi c>0.
Nếu , ta có . Để hàm số đồng biến trên . Chọn C.
Câu 37:
Tìm tất các các giá trị thực của tham số m để hàm số đồng biến trên tập xác định.
 Xem đáp án
Xem đáp án
TXĐ: . Đạo hàm .
Ycbt ( có hữu hạn nghiệm)
Cách giải trắc nghiệm. Quan sát ta nhận thấy các giá trị cần thử là:
ü thuộc B & C nhưng không thuộc A, D.
ü thuộc C & D nhưng không thuộc A, B.
● Với .
Do đó ta loại A và D.
● Với .
Phương trình có nên không thỏa nên loại C.
Câu 38:
Cho hàm số . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên R.
 Xem đáp án
Xem đáp án
Tập xác định . Đạo hàm .
Để hàm số đồng biến trên ( có hữu hạn nghiệm)
Suy ra giá trị lớn nhất của tham số m thỏa mãn ycbt là
Chọn D.
Câu 39:
Cho hàm số với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng
 Xem đáp án
Xem đáp án
TXĐ: . Đạo hàm
Để hàm số đã cho nghịch biến trên khoảng thì ( có hữu hạn nghiệm)
Chọn C.
Sai lầm hay gặp là Để hàm số đã cho nghịch biến trên khoảng thì . Khi đó ra giải ra và chọn D.
Câu 40:
Cho hàm số . Tìm giá trị nhỏ nhất của tham số m để hàm số đồng biến trên R.
 Xem đáp án
Xem đáp án
TXĐ: . Đạo hàm: .
Yêu cầu bài toán ( có hữu hạn nghiệm):
TH1. thì (không thỏa mãn).
TH2.
Suy ra giá trị m nhỏ nhất thỏa mãn bài toán là
Chọn D.
Câu 41:
Cho hàm số . Tìm tất cả các giá trị của tham số thực m để hàm số nghịch biến trên R
 Xem đáp án
Xem đáp án
Ta có
Yêu cầu bài toán ( có hữu hạn nghiệm):
TH1 , khi đó (thỏa mãn).
TH2 .
Hợp hai trường hợp ta được
Chọn C.
Câu 42:
Cho hàm số . Tìm tất cả các giá trị thực của tham số để hàm số đã cho đồng biến trên
 Xem đáp án
Xem đáp án
Ta có
Xét phương trình có
Suy ra phương trình luôn có hai nghiệm với mọi .
Để hàm số đồng biến trên phương trình có hai nghiệm .
Câu 43:
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng để hàm số đồng biến trên khoảng ?
 Xem đáp án
Xem đáp án
Ta có
Xét phương trình có
Suy ra phương trình luôn có hai nghiệm với mọi m.
Theo định lí Viet, ta có
Để hàm số đồng biến trên phương trình có hai nghiệm
Vậy có 1001 số nguyên m thuộc khoảng Chọn B.
Câu 44:
Tìm tất cả các giá trị của m để hàm số nghịch biến trên đoạn
 Xem đáp án
Xem đáp án
Đạo hàm
Ta có .
Do đó luôn có hai nghiệm phân biệt
Bảng biến thiên:
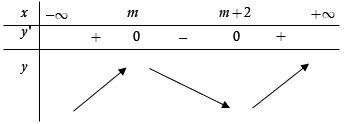
Dựa vào bảng biến thiên, để hàm số nghịch biến trên
Chọn C.
Câu 45:
Cho hàm số . Tìm tất cả các giá trị thực của tham số m để hàm số đã cho đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Ta có
Xét phương trình có
Suy ra phương trình luôn có hai nghiệm với mọi m.
Để hàm số đồng biến trên phương trình có hai nghiệm
. Chọn A.
Câu 46:
 Xem đáp án
Xem đáp án
Ta có .
Yêu cầu bài toán có hai nghiệm phân biệt , thỏa mãn
.
Chọn D.
Câu 47:
Tìm tất cả các giá trị thực của tham số m để hàm số giảm trên đoạn có độ dài lớn nhất bằng 1.
 Xem đáp án
Xem đáp án
Ta có .
Yêu cầu bài toán có hai nghiệm phân biệt thỏa mãn
Chọn D.
Câu 48:
 Xem đáp án
Xem đáp án
Tính
Ta nhớ công thức tính nhanh Nếu hàm bậc ba nghịch biến trên đoạn có độ dài bằng thì phương trình đạo hàm có hai nghiệm và trị tuyệt đối hiệu hai nghiệm bằng "
Với là một số xác định thì m cũng là một số xác định chứ không thể là khoảng => Đáp số phải là A hoặc C .
Thử với m=0 phương trình đạo hàm có hai nghiệm phân biệt và khoảng cách giữa chúng bằng 2.Câu 49:
Cho hàm số với m là tham số thực. Tìm tất cả các giá trị m để hàm số đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Ta có
Nếu có một nghiệm x=0 và y' đổi dấu từ "-" sang "+" khi qua điểm hàm số đồng biến trên khoảng nên đồng biến trên khoảng . Vậy thỏa mãn.
Nếu
Bảng biến thiên
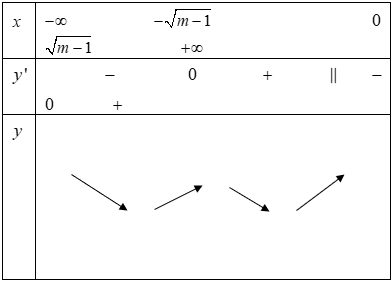
Dựa vào bảng biến tiên, ta có ycbt
Hợp hai trường hợp ta được . Chọn B.
Câu 50:
Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên và đồng biến trên .
 Xem đáp án
Xem đáp án
Ta có
TH1 có một nghiệm x=0 và y' đổi dấu từ "-" sang "+" khi qua điểm hàm số nghịch biến trên và đồng biến trên .
TH2 có ba nghiệm phân biệt
Lập bảng biến thiên ta thấy hàm số đồng biến trên các khoảng và , nghịch biến trên các khoảng và . Do đó trường hợp này không thỏa mãn yêu cầu bài toán.
Cách khác. Để thỏa mãn yêu cầu bài toán thì hàm số chỉ có một cực trị nhưng vấn đề cực trị ở bài này chưa học.
Câu 51:
Cho hàm số . Hỏi có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên khoảng
 Xem đáp án
Xem đáp án
Ta xét hai trường hợp:
Hệ số . Hàm số có đồ thị là một parabol nghịch biến trên khoảng , đồng biến trên khoảng Do đó m=2 thỏa mãn. (Học sinh rất mắc phải sai lầm là không xét trường hợp a=0)
Hệ số . Dựa vào dáng điệu đặc trưng của hàm trùng phương thì yêu cầu bài toán tương đương với đồ thị thàm số có một cực trị và đó là cực tiểu
Vậy
Chọn D.
Câu 52:
 Xem đáp án
Xem đáp án
Ta có .
Với thì => hàm số đã cho nghịch biến trên từng khoảng và .
Ycbt : (thỏa mãn).
Cách 2. Ta có .
Ycbt
Chọn C.
Câu 53:
Cho hàm số với m là tham số thực. Gọi là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S.
 Xem đáp án
Xem đáp án
Ta có .
Để hàm số đồng biến trên từng khoảng xác định thì
Sai lầm hay gặp là cho
Câu 54:
Gọi là tập hợp các số nguyên m để hàm số đồng biến trên khoảng . Tính tổng T của các phần tử trong S
 Xem đáp án
Xem đáp án
TXĐ: . Đạo hàm
Hàm số đồng biến trên khoảng
Chọn D.
Câu 55:
Tập tất cả các giá trị của tham số m để hàm số nghịch biến trên từng khoảng xác định là khoảng . Tính P=b-a.
 Xem đáp án
Xem đáp án
TXĐ: . Đạo hàm
Yêu cầu bài toán
.
Chọn D.
Câu 56:
Gọi S là tập hợp các số nguyên m để hàm số nghịch biến trên khoảng .Tính tổng T của các phần tử trong S
 Xem đáp án
Xem đáp án
TXĐ: . Đạo hàm
Hàm số nghịch biến trên khoảng
Chọn C.
Câu 57:
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng .
 Xem đáp án
Xem đáp án
Đặt , với
Hàm số trở thành
Ta có , do đó đồng biến trên .
Do đó YCBT đồng biến trên khoảng (0;1)
Chọn D.
Câu 58:
Tìm tất cả các giá trị thực của m để hàm số nghịch biến trên khoảng .
 Xem đáp án
Xem đáp án
Đặt , với
Hàm số trở thành .
Ta có , do đó nghịch biến trên .
Do đó YCBT đồng biến trên khoảng (0;1)
Nhận xét. Khi ta đặt ẩn t, nếu t là hàm đồng biến trên khoảng đang xét thì giữ nguyên câu hỏi trong đề bài. Còn nếu t là hàm nghịch biến thì ta làm ngược lại câu hỏi trong đề bài.
Câu 59:
Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên khoảng
 Xem đáp án
Xem đáp án
Đặt , với .
Hàm số trở thành .
Ta có , do đó nghịch biến trên
Do đó YCBT đồng biến trên khoảng
Nhận xét. Do . Và
Câu 60:
Tìm tất các các giá trị thực của tham số m để hàm số nghịch biến trên các khoảng xác định.
 Xem đáp án
Xem đáp án
TXĐ: . Đạo hàm
Yêu cầu bài toán
Chọn B.
Câu 61:
 Xem đáp án
Xem đáp án
Ta có .
Để hàm số đã cho luôn luôn đồng biến trên khi và chỉ khi ( có hữu hạn nghiệm)
(*)
Nếu thì A đúng & C cũng đúng.
Nếu thì
đúng với mọi . Chọn C.
Câu 62:
Tìm tất cả các giá trị của b để hàm số nghịch biến trên toàn trục số.
 Xem đáp án
Xem đáp án
Ta có .
Để hàm số nghịch biến trên .
Chọn A.
Câu 63:
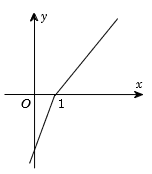
Cho hàm số có đạo hàm xác định, liên tục trên và có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Dựa vào đồ thị hàm số , ta thấy suy ra hàm số đồng biến trên Chọn C.
Câu 64:
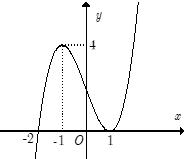
Cho hàm số . Biết rằng hàm số có đạo hàm là và hàm số có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai?
 Xem đáp án
Xem đáp án
Dựa vào đồ thị của hàm số ta thấy:
khi đồng biến trên các khoảng , .
Suy ra A và C đều đúng.
khi nghịch biến trên khoảng .
Suy ra D đúng, B sai. Chọn B.
Câu 65:
 Xem đáp án
Xem đáp án
Ta có
Bảng biến thiên
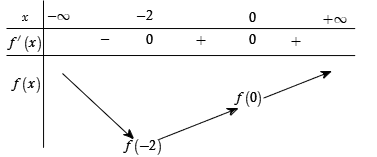
Dựa vào bảng biến thiên, ta có
Hàm số đồng biến trên khoảng
Hàm số nghịch biến trên khoảng .
Chọn A.
