Đáp án đúng là: A

Đáp án đúng là: A

Phương trình mặt cầu có dạng

\[{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\] với \[d = {a^2} + {b^2} + {c^2} - {R^2}.\]

Xét các đáp án, chỉ có đáp án A thỏa mãn, đồng thời ta có thể viết lại như sau:

\[{x^2} + {y^2} + {z^2} - 2x = 0\] hay \[{\left( {x - 1} \right)^2} + {y^2} + {z^2} = 1\].

Đáp án đúng là: C

Ta có: \[{\left( {x - 1} \right)^2} + {y^2} + {\left( {z + 3} \right)^2} = 16\]

\[ \Leftrightarrow {\left( {x - 1} \right)^2} + {y^2} + {\left( {z - \left( { - 3} \right)} \right)^2} = {4^2}\]

Do đó, tâm mặt cầu là \[I\left( {1;0; - 3} \right).\]

Đáp án đúng là: C

Đáp án đúng là: C

Phương trình mặt cầu có dạng

\[{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\] với \[d = {a^2} + {b^2} + {c^2} - {R^2}.\]

Để xác định một mặt cầu khi và chỉ khi \[{R^2} = {a^2} + {b^2} + {c^2} - d > 0.\]

Đáp án đúng là: C

Ta có: \[{x^2} + {y^2} + {z^2} - 4x - 2y + 2z - 3 = 0\]

\[{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 9\].

Do đó, tâm của mặt cầu là \[I\left( {2;1; - 1} \right)\].

Thay \[M\left( {4;2; - 2} \right)\] vào phương trình mặt cầu, ta được

\[{\left( {4 - 2} \right)^2} + {\left( {2 - 1} \right)^2} + {\left( { - 2 + 1} \right)^2} = 6 < 9\].

Do đó điểm M nằm trong mặt cầu.

Đáp án đúng là: B

Ta thay tọa độ các điểm ở từng đáp án vào phương trình mặt cầu \[\left( S \right)\].

Với \[A\left( {3; - 2; - 4} \right)\], có: \[{3^2} + {\left( { - 2} \right)^2} + {\left( { - 4} \right)^2} - 2.3 + 10.\left( { - 2} \right) + 3.\left( { - 4} \right) + 1 = - 8 \ne 0\].

Do đó mặt cầu (S) không đi qua điểm có tọa độ \[\left( {3; - 2; - 4} \right).\]

Với \[B\left( {4; - 1;0} \right)\], có: \[{4^2} + {\left( { - 1} \right)^2} + {0^2} - 2.4 + 10.\left( { - 1} \right) + 3.0 + 1 = 0\].

Do đó, mặt cầu (S) đi qua điểm có tọa độ \[\left( {4; - 1;0} \right).\]

Với \[C\left( {2;1;9} \right)\], có: \[{2^2} + {1^2} + {9^2} - 2.2 + 10.1 + 3.9 + 1 = 120 \ne 0.\]

Do đó, mặt cầu (S) không đi qua điểm có tọa độ \[\left( {2;1;9} \right).\]

Với điểm \[D\left( { - 1;3; - 1} \right)\], có: \[{\left( { - 1} \right)^2} + {3^2} + {\left( { - 1} \right)^2} - 2.\left( { - 1} \right) + 10.3 + 3.\left( { - 1} \right) + 1 = 41 \ne 0\].

Do đó, mặt cầu (S) không đi qua điểm có tọa độ \[\left( { - 1;3; - 1} \right).\]

Đáp án đúng là: B

Phương trình mặt cầu tâm \[I\left( {1; - 2;3} \right)\] bán kính \[R = 3\] là

\[{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = {3^2}\] hay \[{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 9.\]

Đáp án đúng là: A

Ta có: \[{x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0\]

\[ \Leftrightarrow {\left( {x + 4} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 36\]

\[ \Leftrightarrow {\left( {x + 4} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = {6^2}.\]

Vậy ta được Tâm \[I\left( { - 4;3; - 1} \right)\] và bán kính \[R = 6.\]

Đáp án đúng là: D

Xét các đáp án như sau:

• Với \[{x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\] ta có: \[a = - 1,b = - 1,c = 1,d = 4\].

Suy ra \[{a^2} + {b^2} + {c^2} - d = - 1 < 0.\]

Vậy đáp án A không là phương trình mặt cầu.

• Với \[{x^2} + {y^2} + {z^2} + 4x - 2y + 2z + 6 = 0\] ta có: \[a = - 2,b = 1,c = - 1,d = 6\].

Suy ra \[{a^2} + {b^2} + {c^2} - d = 0\]

Vậy đáp án B không là phương trình mặt cầu.

• Với \[{x^2} + {y^2} + {z^2} + 2x - 6y + 4z + 14 = 0\] có: \[a = - 1,b = 3,c = - 2,d = 14\].

Suy ra \[{a^2} + {b^2} + {c^2} - d = 0\]

Vậy đáp án C không là phương trình mặt cầu.

• Với \[{x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0\] có: \[a = - 4,b = 3,c = - 1,d = - 10\].

Suy ra \[{a^2} + {b^2} + {c^2} - d = 36 > 0.\]

Vậy đáp án D là phương trình của một mặt cầu.

Đáp án đúng là: D

Gọi \[H\] là hình chiếu của \[I\] lên trục \[Oz\] thì \[H\left( {0;0;2} \right)\].

Từ đó, \[R = IH = \sqrt {{{\left( {3 - 0} \right)}^2} + {{\left( {4 - 0} \right)}^2} + {{\left( {2 - 2} \right)}^2}} = 5.\]

Vậy phương trình mặt cầu tâm \[I\] tiếp xúc với trục \[Oz\] là

\[{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z - 2} \right)^2} = 25.\]

Đáp án đúng là: A

Tâm \[I\] của mặt cầu là trung điểm của \[AB\] do đó \[I\left( {2;1; - 1} \right)\].

Ta có: \[R = IA = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {1 - 0} \right)}^2} + {{\left( { - 1 - \left( { - 3} \right)} \right)}^2}} = \sqrt 6 .\]

Vậy phương trình mặt cầu đường kính \[AB\] là

\[{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 6\] hay \[{x^2} + {y^2} + {z^2} - 4x - 2y + 2z = 0.\]

Đáp án đúng là: A

Ta có: \[\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 2y - 2z - 6 = 0\]

\[{\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 9.\]

Vậy tâm của mặt cầu là \[I\left( {1; - 1;1} \right)\] và bán kính \[R = 3.\]

Để \[\left( P \right)\] tiếp xúc với \[\left( S \right)\] thì \[d\left( {I,\left( P \right)} \right) = 3\].

Suy ra \[d\left( {I,\left( P \right)} \right) = \frac{{\left| {2.1 + 2.\left( { - 1} \right) + 1 - {m^2} + 4m - 5} \right|}}{{\sqrt {{2^2} + {2^2} + {1^2}} }} = \frac{{\left| { - {m^2} + 4m - 4} \right|}}{3} = 3\].

Hay \[\left| { - {m^2} + 4m - 4} \right| = 9\] \[ \Leftrightarrow \left[ \begin{array}{l} - {m^2} + 4m - 4 = 9\\ - {m^2} + 4m - 4 = - 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - {m^2} + 4m - 13 = 0\\ - {m^2} + 4m + 5 = 0\end{array} \right.\]

Giải phương trình, ta có nghiệm \[m = - 1\] hoặc \[m = 5.\]

Đáp án đúng là: D

Ta có: \[{x^2} + {y^2} + z{}^2 - 4x + 1 = 0\]

\[ \Leftrightarrow {\left( {x - 2} \right)^2} + {y^2} + z{}^2 = 3\].

Vậy mặt cầu có tâm \[I\left( {2;0;0} \right)\] và bán kính \[R = \sqrt 3 \].

Đáp án đúng là: A

Ta có: \[{x^2} + {y^2} + {z^2} + 4mx + 2my - 2mz + 9{m^2} - 28 = 0\] với \[a = - 2m,b = - m,c = m\] và \[d = 9{m^2} - 28\].

Để phương trình là một mặt cầu thì \[{a^2} + {b^2} + {c^2} - d > 0\]

\[ \Leftrightarrow 4{m^2} + {m^2} + {m^2} - 9{m^2} + 28 > 0\]

\[ \Leftrightarrow - 3{m^2} + 28 > 0\]

\[ \Leftrightarrow {m^2} < \frac{{28}}{3}\]

\[ \Leftrightarrow - \sqrt {\frac{{28}}{3}} < m < \sqrt {\frac{{28}}{3}} \]

\[ \Leftrightarrow - 3,055 < m < 3,055\].

Mà \[m \in \mathbb{Z}\] nên \[m \in \left\{ { - 3; - 2; - 1;0;1;2;3} \right\}.\]

Vậy có 7 giá trị thỏa mãn.

Đáp án đúng là: D

Gọi \[A\left( {a;0;0} \right),B\left( {0;b;0} \right),C\left( {0;0;c} \right)\].

Tam giác \[ABC\] có trọng tâm \[G\left( { - 6; - 12;18} \right)\] nên ta có:

\[\left\{ \begin{array}{l}\frac{{a + 0 + 0}}{3} = - 6\\\frac{{0 + b + 0}}{3} = - 12\\\frac{{0 + 0 + c}}{3} = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 18\\b = - 36\\c = 54\end{array} \right.\].

Suy ra \[A\left( { - 18;0;0} \right),B\left( {0; - 36;0} \right),C\left( {0;0;54} \right)\].

Gọi \[I\left( {x;y;z} \right)\], ta có: \[\left\{ \begin{array}{l}IO = IA\\IA = IB\\IB = IC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}I{O^2} = I{A^2}\\I{A^2} = I{B^2}\\I{B^2} = I{C^2}\end{array} \right.\].

\[ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} = {\left( {x + 18} \right)^2} + {y^2} + {z^2}\\{\left( {x + 18} \right)^2} + {y^2} + {z^2} = {x^2} + {\left( {y + 36} \right)^2} + {z^2}\\{x^2} + {\left( {y + 36} \right)^2} + {z^2} = {x^2} + {y^2} + {\left( {z - 54} \right)^2}\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}36x + 324 = 0\\36x + 324 - 72y - 1296 = 0\\72y + 1296 + 108z - 2916 = 0\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}x = - 9\\y = - 18\\z = 27\end{array} \right.\].

Vậy tâm của mặt cầu là \[I\left( { - 9; - 18;27} \right).\]

Đáp án đúng là: C

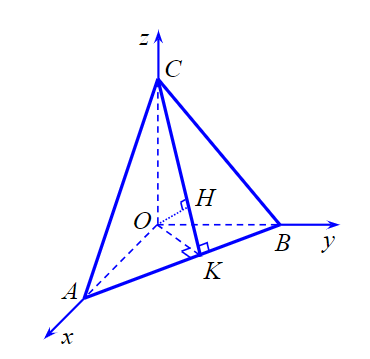
Ta có

\[H\] là trực tâm của tam giác \[ABC\], suy ra \[OH \bot \left( {ABC} \right)\].

Thật vậy:

\[\left\{ \begin{array}{l}OC \bot OA\\OC \bot OB\end{array} \right. \Rightarrow OC \bot AB\] (1)

Mà \[CH \bot AB\] (vì \[H\] là trực tâm tam giác \[ABC\]) (2).

Từ (1) và (2) suy ra \[AB \bot \left( {OHC} \right)\]\[ \Rightarrow AB \bot OH\].

Tương tự, ta suy ra \[BC \bot \left( {OAH} \right)\]\[ \Rightarrow BC \bot OH.\]

Từ đây suy ra \[OH \bot \left( {ABC} \right).\]

Khi đó, mặt cầu tâm \[O\] tiếp xúc mặt phẳng \[\left( {ABC} \right)\] có bán kính \[R = OH = 3.\]

Vậy mặt cầu tâm \[O\] và tiếp xúc với mặt phẳng \[\left( \alpha \right)\] là \[{x^2} + {y^2} + {z^2} = 9.\]

Đáp án đúng là: B

Giả sử \[M\left( {x;y;z} \right).\]

Ta có: \[M{A^2} = {\left( {x - 1} \right)^2} + {y^2} + {z^2}\];

\[M{B^2} = {x^2} + {\left( {y - 2} \right)^2} + {z^2}\];

\[M{C^2} = {x^2} + {y^2} + {\left( {z - 3} \right)^2}\].

Có \[M{A^2} = M{B^2} + M{C^2}\]

\[ \Leftrightarrow {\left( {x - 1} \right)^2} + {y^2} + {z^2} = {x^2} + {\left( {y - 2} \right)^2} + {z^2} + {x^2} + {y^2} + {\left( {z - 3} \right)^2}\].

\[ \Leftrightarrow {x^2} + 2x - 1 + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 0\]

\[ \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 2\].

Vậy tập hợp các điểm \[M\] thỏa mãn \[M{A^2} = M{B^2} + M{C^2}\] là mặt cầu có bán kính \[R = \sqrt 2 .\]

Đáp án đúng là: B

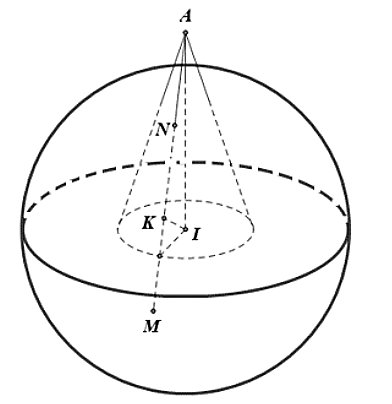
Gọi hình chiếu vuông góc của

\[I\] trên \[MN\] là \[K\].

Dễ thấy \[AN = NK = \frac{1}{3}AM\], mặt cầu \[\left( S \right)\] có tâm \[I\left( {1;2;3} \right)\] và bán kính \[R = 5.\]

Có \[AM.AN = A{I^2} - {R^2} = 4\]\[ \Rightarrow A{N^2} = \frac{4}{3}\]

\[ \Rightarrow AN = NK = \frac{{2\sqrt 3 }}{3}\]\[ \Rightarrow IK = \sqrt {I{N^2} - K{N^2}} = \frac{{\sqrt {213} }}{3}.\]

Nhận thấy mặt cầu đồng tâm với mặt cầu \[\left( S \right)\] và tiếp xúc với các đường sinh của hình nón \[\left( H \right)\] chính là mặt cầu tâm \[I\left( {1;2;3} \right)\], bán kính \[IK = \frac{{\sqrt {213} }}{3}.\]

Vậy phương trình mặt cầu cần tìm là: \[{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = \frac{{71}}{3}.\]

Đáp án đúng là: B

Ta có: \[\left( S \right):\]\[{x^2} + {y^2} + {z^2} + 2x - 4y - 6z + m - 3 = 0\]

\[ \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 17 - m.\]

\[\left( S \right)\] là phương trình của mặt cầu thì \[17 - m > 0 \Leftrightarrow m < 17.\]

Khi đó mặt cầu có tâm \[I\left( { - 1;2;3} \right)\] và bán kính \[R = \sqrt {17 - m} \].

Để mặt phẳng \[\left( \beta \right):\]\[2x - y + 2z - 8 = 0\] cắt \[\left( S \right)\] theo thiết diện là một đường tròn có chu vi bằng \[8\pi \] thì đường tròn đó có bán kính \[r = 4\].

Ta có: \[d\left( {I,\left( \beta \right)} \right) = \frac{{\left| {2.\left( { - 1} \right) - 2 + 2.3 - 8} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}} }} = 2\].

Ta có: \[{R^2} = {d^2}\left( {I,\left( \beta \right)} \right) + {r^2}\] \[ \Leftrightarrow 17 - m = 2 + 16\]\[ \Leftrightarrow m = - 1{\rm{ }}\left( {TM} \right).\]