Chuyên đề Toán 12 Bài 2: Mặt trụ có đáp án
-
635 lượt thi
-
51 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Câu 2:
 Xem đáp án
Xem đáp án
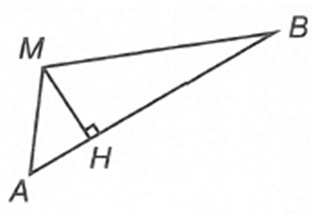
Vì AB cố định nên diện tích tam giác MAB không đổi khi d (M,AB) = const hay M thuộc mặt trụ trục là đường thẳng AB.
Câu 3:
 Xem đáp án
Xem đáp án
Chọn A
Vì bán kính đáy R=1, thể tích
Vậy diện tích toàn phần của hình trụ là
Câu 4:
 Xem đáp án
Xem đáp án
Chọn D
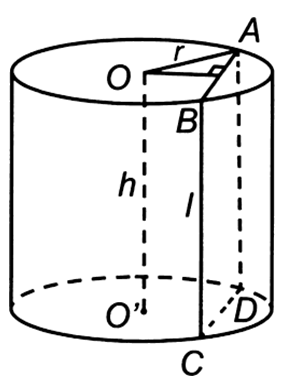
Thiết diện thu được là hình chữ nhật ABCD và OO' // (ABCD), gọi I là trung điểm của AB
Ta cóCâu 5:
 Xem đáp án
Xem đáp án
Chọn C
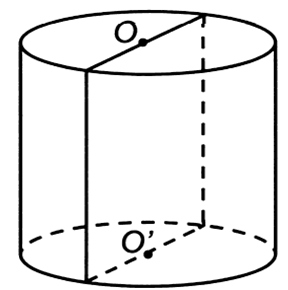
Do thiết diện là một hình vuông cạnh 2a nên chiều cao h của hình trụ bằng 2a và đường kính mặt đáy bằng 2a suy ra bán kính đáy r = a. Khi đó diện tích xung quanh của hình trụ là
Câu 6:
Cho hình trụ có diện tích xung quanh bằng và độ dài đường sinh bằng đường kính của đường tròn đáy. Bán kính r của đường tròn đáy là
 Xem đáp án
Xem đáp án
Chọn D
Theo giả thiết độ dài đường sinh l = 2r
Ta cóCâu 7:
 Xem đáp án
Xem đáp án
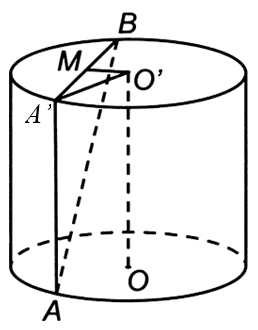
Gọi r là bán kính đáy.
Do thiết diện qua trục là hình vuông nên độ dài đường sinh bằng 2r.
Dựng đường sinh AA'.
Gọi M là trung điểm của A' B
Ta có
Mặt khác
Câu 8:
Cho hình trụ có hai đáy là hai hình tròn (O) và (O'), chiều cao 2R và bán kính đáy R. Một mặt phẳng đi qua trung điểm của OO' và tạo với OO' một góc 30o. Hỏi cắt đường tròn đáy theo một dây cung có độ dài bằng bao nhiêu?
 Xem đáp án
Xem đáp án
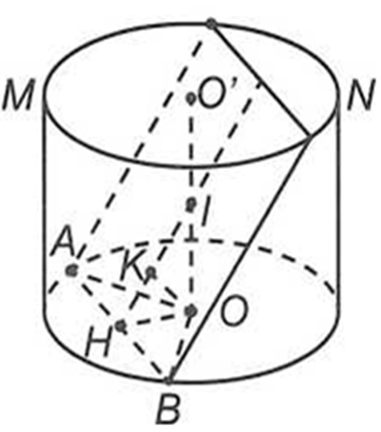
Gọi I là trung điểm của OO'
Khi đó, mặt phẳng
Hạ . Dễ thấy H là trung điểm của AB và
Suy ra (vì vuông tại O)
Khi đó . Vì vuông tại O nênCâu 9:
 Xem đáp án
Xem đáp án
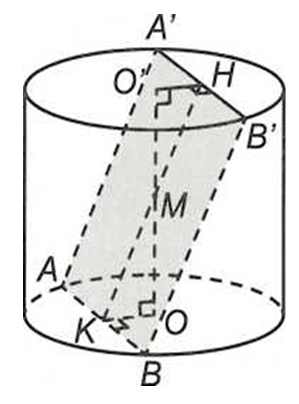
Diện tích hình chữ nhật ABB'A' bằng 60 (cm2)
nên AB.BB' = 60
Ta có
Chiều cao hình trụ bằng (cm) nên
Câu 10:
 Xem đáp án
Xem đáp án
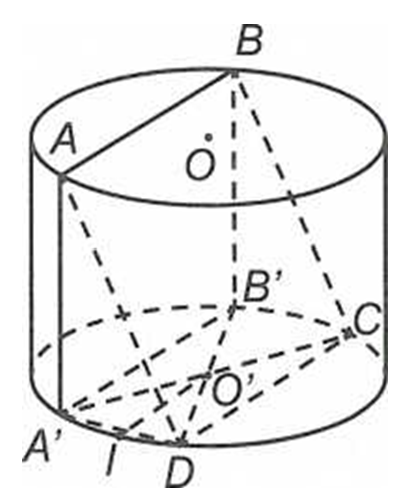
Đặt
Gọi A', B' lần lượt là hình chiếu vuông góc của A, B lên mặt đáy của hình trụ.
Xét tam giác AA'D vuông tại A' ta có
Mặt khác, gọi I là trung điểm của A'D thì ta có:
Do đóCâu 11:
 Xem đáp án
Xem đáp án
Chọn A
Câu 12:
 Xem đáp án
Xem đáp án
Chọn B
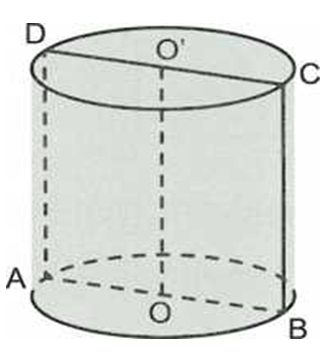
Gọi ABCD là thiết diện qua trục của hình trụ, ta có ABCD là hình chữ nhật. Từ giả thiết suy ra AB = 2a và
Vậy thể tích khối trụ đã cho bằng:
Câu 13:
 Xem đáp án
Xem đáp án
Chọn C
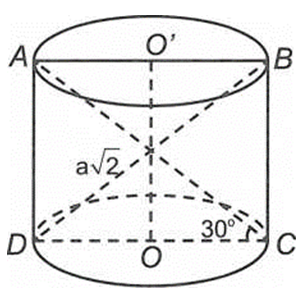
Ta có
Mặt khác xét tam giác ADC vuông tại D, ta có
và
NênCâu 14:
 Xem đáp án
Xem đáp án
Chọn B
Khối trụ tạo thành khi cho hình chữ nhật ABCD quay xung quanh cạnh AB có bán kính đáy và chiều cao lần lượt là
Khi đó, thể tích của khối trụ này là
Khối trụ tạo thành khi cho hình chữ nhật ABCD quay xung quanh cạnh AD có bán kính đáy và chiều cao lần lượt là
Khi đó, thể tích của khối trụ này là
VậyCâu 15:
 Xem đáp án
Xem đáp án
Chọn B
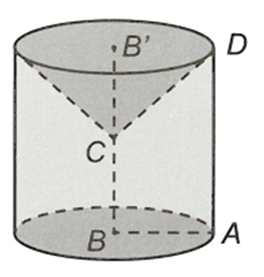
Thể tích . Trong đó là thể tích khối trụ có bán kính đáy là BA = a và chiều cao AD = 2a. là thể tích khối nón có bán kính đáy là B'D = a và chiều cao CB' = a
Khi đóCâu 16:
 Xem đáp án
Xem đáp án
Chọn B
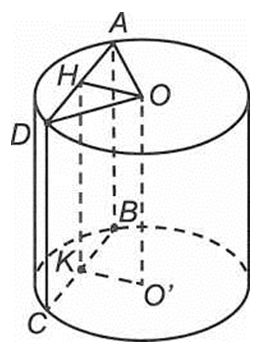
Giả sử hình vuông ABCD là thiết diện của hình trụ cắt bởi (P) như hình vẽ.
Gọi H, K lần lượt là trung điểm AD, BC.
Ta có
Do đó
Suy ra
Vậy nênCâu 17:
 Xem đáp án
Xem đáp án
Chọn D
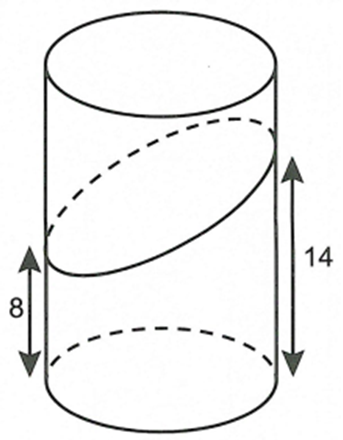
Gọi V1; V2 lần lượt là thể tích khối nhỏ và khối lớn.
Ta có thể tích khối trụ là (với R là bán kính khối trụ).
Thể tích
VậyCâu 18:
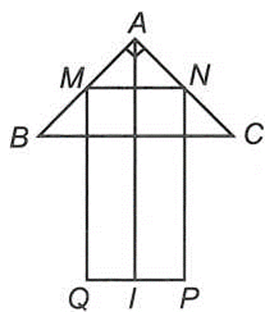
 Xem đáp án
Xem đáp án
Chọn D
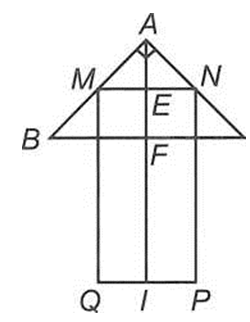
Ta có
Gọi E, F lần lượt là trung điểm MN và BC.
Vậy thể tích cần tìm là tổng thể tích của khối nón có chiều cao là AF bán kính đáy FB và thề tích khối trụ có chiều cao IF bán kính IQ.
Câu 19:
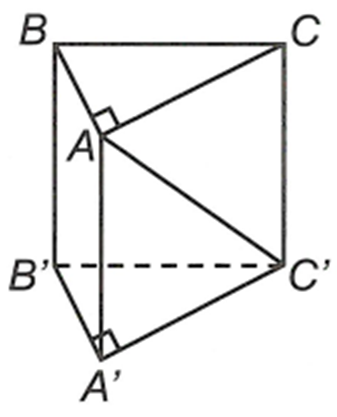
 Xem đáp án
Xem đáp án
Chọn C
Gọi bán kính của hình trụ là R.
Ta có
Lại có tam giác ABC là tam giác vuông cân tại A nên do đó hay góc giữa AC’ và mặt phẳng (BCC'B') làXét tam giác AIC' ta có
Xét tam giác CIC' ta có
Thể tích khối trụ ngoại tiếp lăng trụ ABC.A'B'C' là
Câu 20:
 Xem đáp án
Xem đáp án
Chọn C
Gọi r là bán kính bể dự định làm, h là chiều cao các bể.
Ta có:Câu 21:
Cho một tấm bìa hình chữ nhật có kích thước 3a, 6a. Người ta muốn tạo tấm bìa đó thành 4 hình không đáy như hình vẽ dưới đây, trong đó có hai hình trụ lần lượt có chiều cao 3a, 6a và hai hình lăng trụ tam giác đều có chiều cao lần lượt 3a, 6a. Trong bốn hình H1, H2, H3, H4 lần lượt theo thứ tự có thể tích lớn nhất và nhỏ nhất là
 Xem đáp án
Xem đáp án
Chọn A
Gọi R1 , R2 lần lượt là bán kính của hai hình trụ ở hình H1, H2.
Gọi lần lượt là thể tích của hai hình trụ ở hình H1, H2.
lần lượt là chu vi đáy của hai hình trụ ở hình H1, H2.
Ta có:
Do hai hình H3, H4 là hai hình lăng trụ tam giác đều nên ta có độ dài các cạnh đáy của hai hình H3, H4 lần lượt là 2a ;a.
Thể tích hình H3, H4 lần lượt là:
Từ đó ta có hai hình có thể tích lớn nhất và nhỏ nhất lần lượt theo thứ tự là H1, H4.
Câu 22:
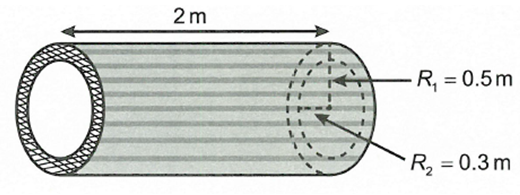
 Xem đáp án
Xem đáp án
Chọn A
Ta có:
Câu 23:
 Xem đáp án
Xem đáp án
Chọn B
Gọi O, O' lần lượt là tâm đáy trên và đáy dưới của hình trụ.
Ta có:
Ta có thể tích khối trụ là:
Câu 24:
 Xem đáp án
Xem đáp án
Chọn C
Gọi thể tích của toàn bộ khối đồ chơi là V, thể tích của khối dưới và khối trên lần lượt là V1 và V2.
Ta có:
Mà nên
Câu 25:
 Xem đáp án
Xem đáp án
Chọn C
Thể tích chất lỏng
Khi lật ngược bình, thể tích phần hình nón chứa chất lỏng là
Mà Do dó
Theo bài raCâu 26:
Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có thể tích V nhất định. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tỉ số sao cho chi phí vật liệu Sản xuất thùng là nhỏ nhất là bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn C
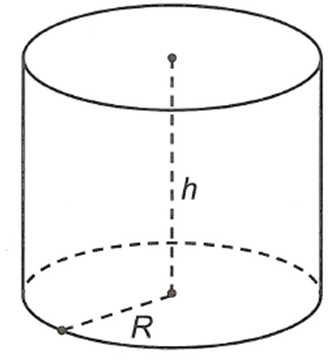
Ta có
Giá thành vật liệu để làm chiếc thùng là trong đó A là giá của một đơn vị diện tích vật liệu làm mặt xung quanh của thùng. Áp dụng bất đẳng thức Cô-si cho các số dương được
Dấu “= ” xảy ra khi
Vậy chi phí vật liệu sản xuất thùng là nhỏ nhất khiCâu 29:
 Xem đáp án
Xem đáp án
Chọn A
Câu 30:
 Xem đáp án
Xem đáp án
Chọn D
Câu 31:
 Xem đáp án
Xem đáp án
Chọn A
Câu 32:
 Xem đáp án
Xem đáp án
Chọn C
Câu 33:

 Xem đáp án
Xem đáp án
Chọn A
Câu 34:
 Xem đáp án
Xem đáp án
Chọn C
Câu 35:
 Xem đáp án
Xem đáp án
Chọn A
Câu 36:
 Xem đáp án
Xem đáp án
Chọn B
Câu 37:
Cho hình lăng trụ tam giác đều ABC.A'B'C' có độ dài cạnh đáy bằng a, chiều cao là h. Thể tích V của khối trụ ngoại tiếp hình lăng trụ là
 Xem đáp án
Xem đáp án
Chọn B
Câu 38:
 Xem đáp án
Xem đáp án
Chọn B
Câu 39:
 Xem đáp án
Xem đáp án
Chọn C
Câu 40:
 Xem đáp án
Xem đáp án
Chọn D
Câu 41:
 Xem đáp án
Xem đáp án
Chọn A
Câu 42:
 Xem đáp án
Xem đáp án
Chọn B
Câu 43:
 Xem đáp án
Xem đáp án
Chọn A
Câu 44:
 Xem đáp án
Xem đáp án
Chọn C
Câu 45:
Ông A dự định làm một cái bể nuôi cá có dạng hình trụ (không có nắp) với dung tích 200dm3. Bán kính r của đáy hình trụ để ông A sử dụng nguyên liệu ít tốn kém nhất là
 Xem đáp án
Xem đáp án
Chọn A
Câu 46:
 Xem đáp án
Xem đáp án
Chọn D
Câu 47:
 Xem đáp án
Xem đáp án
Chọn B
Câu 48:
 Xem đáp án
Xem đáp án
Chọn A
Câu 49:
 Xem đáp án
Xem đáp án
Chọn A
Câu 50:
 Xem đáp án
Xem đáp án
Chọn C
Câu 51:
 Xem đáp án
Xem đáp án
Chọn D
