Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án (Đề 15)
-
4207 lượt thi
-
35 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số \[y = f\left( x \right)\]có đạo hàm trên \[\mathbb{R}\]. Xét tính đúng sai của các mệnh đề sau:
 Xem đáp án
Xem đáp án
Lời giải
Câu 2:
 Xem đáp án
Xem đáp án
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải
Câu 5:
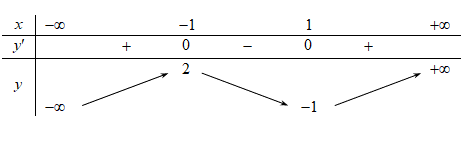
 Xem đáp án
Xem đáp án
Lời giải
Câu 6:
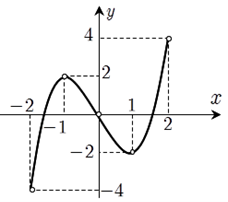
 Xem đáp án
Xem đáp án
Lời giải
Câu 7:
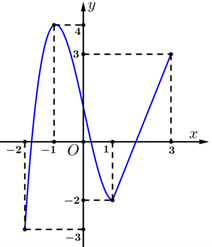
 Xem đáp án
Xem đáp án
Lời giải
Câu 8:
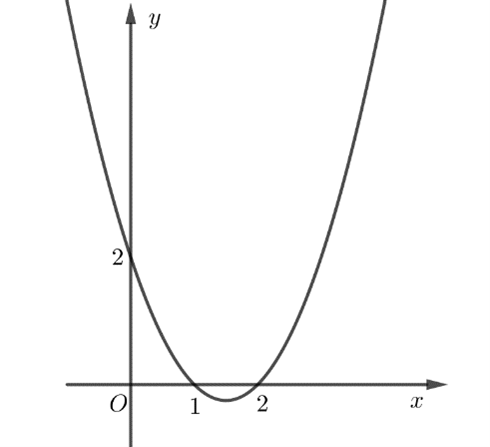
Cho hàm số \(y = f\left( x \right)\)có đồ thị như hình vẽ.
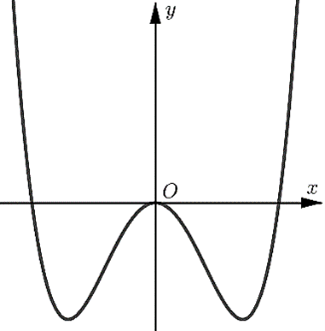
 Xem đáp án
Xem đáp án
Lời giải
Câu 9:
 Xem đáp án
Xem đáp án
Lời giải
Câu 10:
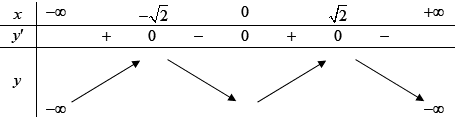
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau
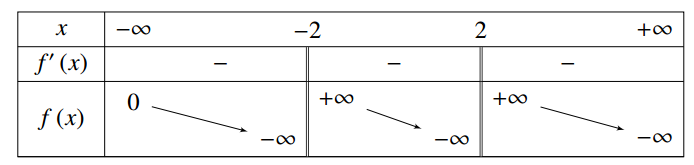
 Xem đáp án
Xem đáp án
Lời giải
Câu 11:
 Xem đáp án
Xem đáp án
Lời giải
Câu 12:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ
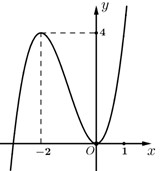
 Xem đáp án
Xem đáp án
Lời giải
Câu 13:
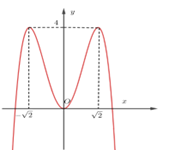
 Xem đáp án
Xem đáp án
Lời giải
Câu 14:
Cho hàm số \(f\left( x \right)\)có bảng biến thiên như sau:
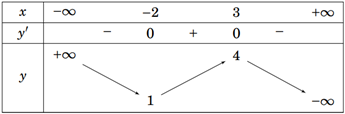
 Xem đáp án
Xem đáp án
Lời giải
Câu 15:
 Xem đáp án
Xem đáp án
Lời giải
Câu 16:
 Xem đáp án
Xem đáp án
Lời giải
Câu 17:
 Xem đáp án
Xem đáp án
Lời giải
Câu 18:
 Xem đáp án
Xem đáp án
Lời giải
Câu 19:
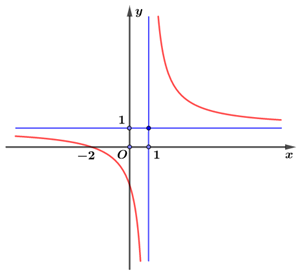
 Xem đáp án
Xem đáp án
Lời giải
Câu 20:
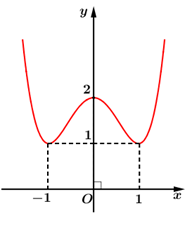
 Xem đáp án
Xem đáp án
Lời giải
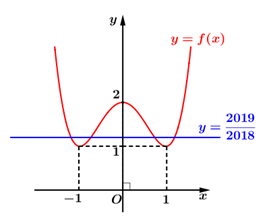
Câu 21:
 Xem đáp án
Xem đáp án
Lời giải
Câu 22:
Cho hàm số \(y = f\left( x \right) = \frac{{ax + 3}}{{2x - b}}\)có bảng biến thiên như sau
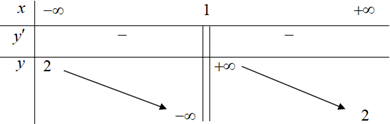
 Xem đáp án
Xem đáp án
Lời giải
Câu 23:
 Xem đáp án
Xem đáp án
Lời giải
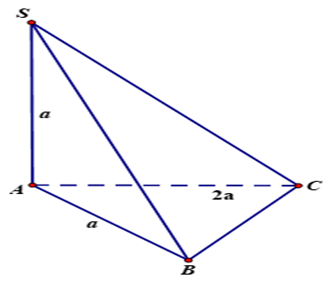
Câu 24:
 Xem đáp án
Xem đáp án
Lời giải

Câu 25:
 Xem đáp án
Xem đáp án
Lời giải
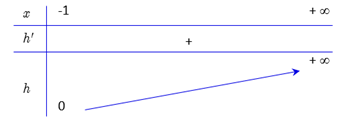
Từ bảng biến thiên ta có\(\left( * \right)\; \Leftrightarrow \;2m\; \le \;0\; \Leftrightarrow \;m\; \le \;0\) hay \(m \in \left( { - \infty ;0} \right]\)
Câu 26:
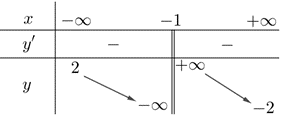
 Xem đáp án
Xem đáp án
Lời giải
Câu 27:
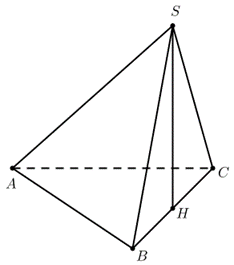
 Xem đáp án
Xem đáp án
Lời giải
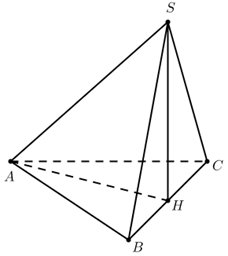
Câu 28:
 Xem đáp án
Xem đáp án
Lời giải
Câu 29:
 Xem đáp án
Xem đáp án
Lời giải
Câu 30:
 Xem đáp án
Xem đáp án
Lời giải
![]()
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
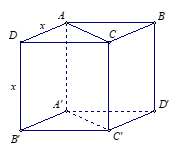
Câu 32:
 Xem đáp án
Xem đáp án
Lời giải
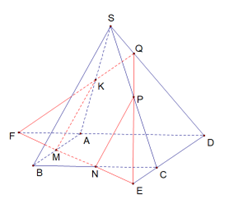
Câu 33:
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị hàm \(f'\left( x \right)\) như hình dưới.
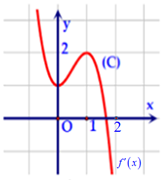
 Xem đáp án
Xem đáp án
Lời giải
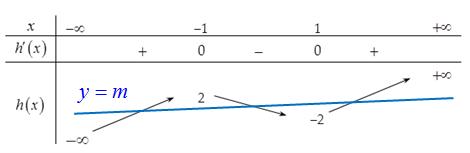
Câu 34:
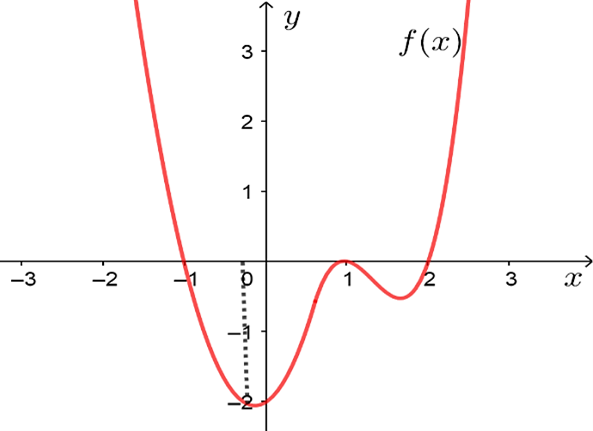
 Xem đáp án
Xem đáp án
Lời giải
Câu 35:
 Xem đáp án
Xem đáp án
Lời giải