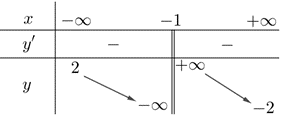
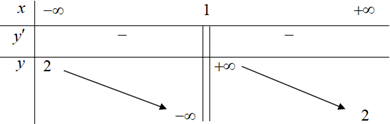
Lời giải
Chọn B
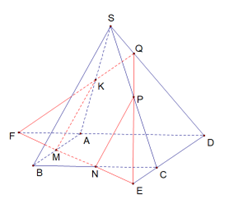
Trong mặt phẳng \(\left( {ABCD} \right)\), kéo dài \(MN\) cắt \(DA\), \(DC\) lần lượt tại \(F\), \(E\).
Trong mặt phẳng \(\left( {SAD} \right)\), gọi \(FK \cap SD = Q\). Trong mặt phẳng \(\left( {SCD} \right)\), gọi \(QE \cap SC = P\).
Suy ra thiết diện là ngũ giác \(MNPQK\) và \(MN{\rm{//}}AC\;{\rm{//\;}}PK\).
Đặt \(h = d\left( {S,\left( {ABCD} \right)} \right)\) \( \Rightarrow d\left( {K,\left( {ABCD} \right)} \right) = d\left( {P,\left( {ABCD} \right)} \right) = \frac{1}{2}h\)
Ta có: \(FA = BN = \frac{1}{2}AD \Rightarrow \frac{{FD}}{{FA}} = 3\).
Áp dụng định lý Menelaus cho tam giác \(SAD\), suy ra
\(\frac{{QS}}{{QD}}.\frac{{FD}}{{FA}}.\frac{{KA}}{{KS}} = 1 \Rightarrow \frac{{QS}}{{QD}} = \frac{1}{3} \Rightarrow \frac{{QD}}{{SD}} = \frac{3}{4} \Rightarrow d\left( {Q,\left( {ABCD} \right)} \right) = \frac{3}{4}h\)
Mặt khác: \({S_{FAM}} = {S_{NCE}} = {S_{BMN}} = \frac{1}{4}{S_{ABC}} = \frac{1}{8}{S_{ABCD}} \Rightarrow {S_{DEF}} = \frac{9}{8}{S_{ABCD}}\)
Suy ra thể tích của khối đa diện không chứa đỉnh S là
\(V = {V_{QDEF}} - {V_{KAMF}} - {V_{PECN}} = \frac{1}{3}\left( {\frac{3}{4}h.\frac{9}{8}S - \frac{1}{2}h.\frac{1}{8}S - \frac{1}{2}h.\frac{1}{8}S} \right)\)
\( = \frac{1}{3}.\frac{{23}}{{32}}.h.{S_{ABCD}} = \frac{{23}}{{32}}{V_{ABCD}} = {V_2}\)
\( \Rightarrow {V_1} = \frac{9}{{32}} \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{9}{{23}}\)
Giải bởi Vietjack
