Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
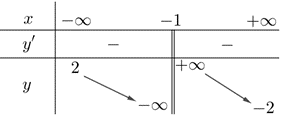
Cho hàm số \[y = f\left( x \right)\]có đạo hàm trên \[\mathbb{R}\]. Xét tính đúng sai của các mệnh đề sau:
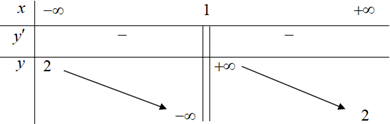
Cho hàm số \(y = f\left( x \right) = \frac{{ax + 3}}{{2x - b}}\)có bảng biến thiên như sau