Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án (Đề 5)
-
4209 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Chọn B
Tập xác định \(D = \mathbb{R}\).
Ta có \(y' = 4{x^3} + 4x = 4x({x^2} + 1)\); \(y' = 0 \Leftrightarrow x = 0\).
Bảng biến thiên
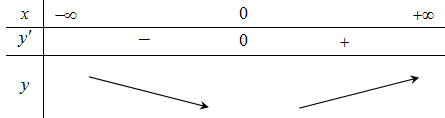
Hàm số đồng biến trên khoảng \((0\,;\, + \infty )\).
Câu 2:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.
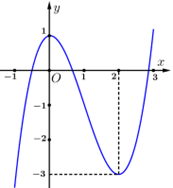
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn B
Quan sát bảng đồ thị, ta thấy hàm số nghịch biến trên các khoảng \(\left( {0;2} \right).\)
Nên chọn đáp án
Câu 3:
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\)và có bảng biến thiên như sau:
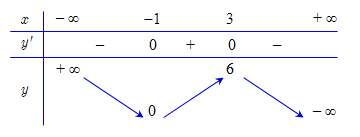
Khẳng định nào sau đây là sai về sự biến thiên của hàm số \(y = f\left( x \right)\)?
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
Từ bảng biến thiên ta thấy \(y' < 0\)với mọi \(x > 3\), suy ra hàm số nghịch biến trên khoảng \(\left( {3;6} \right)\), do đó hàm số không thể đồng biến trên khoảng \(\left( {0;6} \right)\).
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
\(f'\left( x \right) = 4{x^3} - 24{x^2} = 4{x^2}\left( {x - 6} \right)\) ; \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 6\end{array} \right.\).
Bảng biến thiên
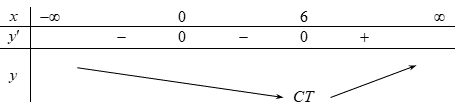
Từ bảng biến thiên ta thấy hàm số nhận điểm \(x = 6\)làm điểm cực tiểu.
Câu 5:
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ { - \sqrt 3 ;\sqrt 3 } \right]\) và có đồ thị hàm số như hình vẽ sau
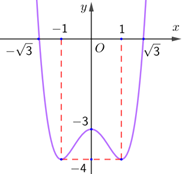
Điểm cực đại của đồ thị hàm số đã cho là
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
Dựa vào đồ thị của hàm số, điểm cực đại của đồ thị hàm số là \(N\left( {0; - 1} \right)\).
Câu 6:
 Xem đáp án
Xem đáp án
Lời giải
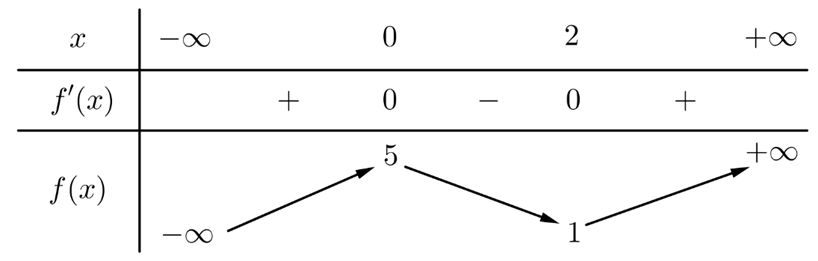
Dựa vào bảng biến thiên, ta thấy hàm số có giá trị cực đại bằng \(5\) tại \(x = 0\) và có giá trị cực tiểu bằng \(1\) tại \(x = 2.\) Từ các đáp án A, B, C, D ta chọn
Câu 7:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
Xét hàm số \(y = {x^3} + 3{x^2} - 9x + 1\)xác định và liên tục trên đoạn \(\left[ { - 4;4} \right]\).
Ta có \(y' = 3{x^2} + 6x - 9\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ { - 4;4} \right]\\x = - 3 \in \left[ { - 4;4} \right]\end{array} \right.\).
Khi đó \(y\left( { - 4} \right) = 21\), \(y\left( { - 3} \right) = 28\), \(y\left( 1 \right) = - 4\), \(y\left( 4 \right) = 77\).
Vậy giá trị nhỏ nhất của hàm số \(y = {x^3} + 3{x^2} - 9x + 1\)trên đoạn \(\left[ { - 4;4} \right]\)là \( - 4\).
Câu 8:
 Xem đáp án
Xem đáp án
Lời giải
Chọn C
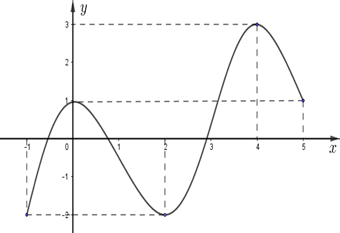
Nhìn đồ thị của hàm số\(f(x)\) trên đoạn \(\left[ { - 1\,;5} \right]\)ta thấy:
\(M = \mathop {\max }\limits_{\left[ { - 1;5} \right]} f(x) = 3\)và \(m = \mathop {\min }\limits_{\left[ { - 1;5} \right]} f(x) = - 2\)nên \(M + m = 1\).Câu 9:
 Xem đáp án
Xem đáp án
Chọn A
TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có : \(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{x}{{x - 1}} = + \infty \).
Suy ra đồ thị hàm số có tiệm cận đứng \(x = 1\).
Câu 10:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
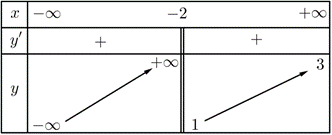
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
Ta có \(\mathop {\lim }\limits_{x \to \, + \infty } y = 3 \Rightarrow \) Đồ thị hàm số có tiệm cận ngang \(y = 3\).
\(\mathop {\lim }\limits_{x \to \,{{\left( { - 2} \right)}^ - }} y = + \infty \Rightarrow \) Đồ thị hàm số có tiệm cận đứng \(x = - 2\).
Vậy đồ thị hàm số có \(2\) đường tiệm cận.
Câu 11:
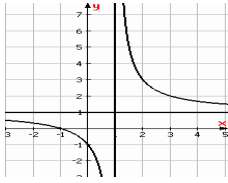
Đồ thị sau đây là của hàm số nào?
 Xem đáp án
Xem đáp án
Chọn C
Từ hình vẽ cho thấy đồ thị hàm số đã cho có đường tiệm cận đứng: \(x = 1\) và đường tiệm cận
ngang: \(y = 1\).
Câu 12:
 Xem đáp án
Xem đáp án
Lời giải
Chọn C
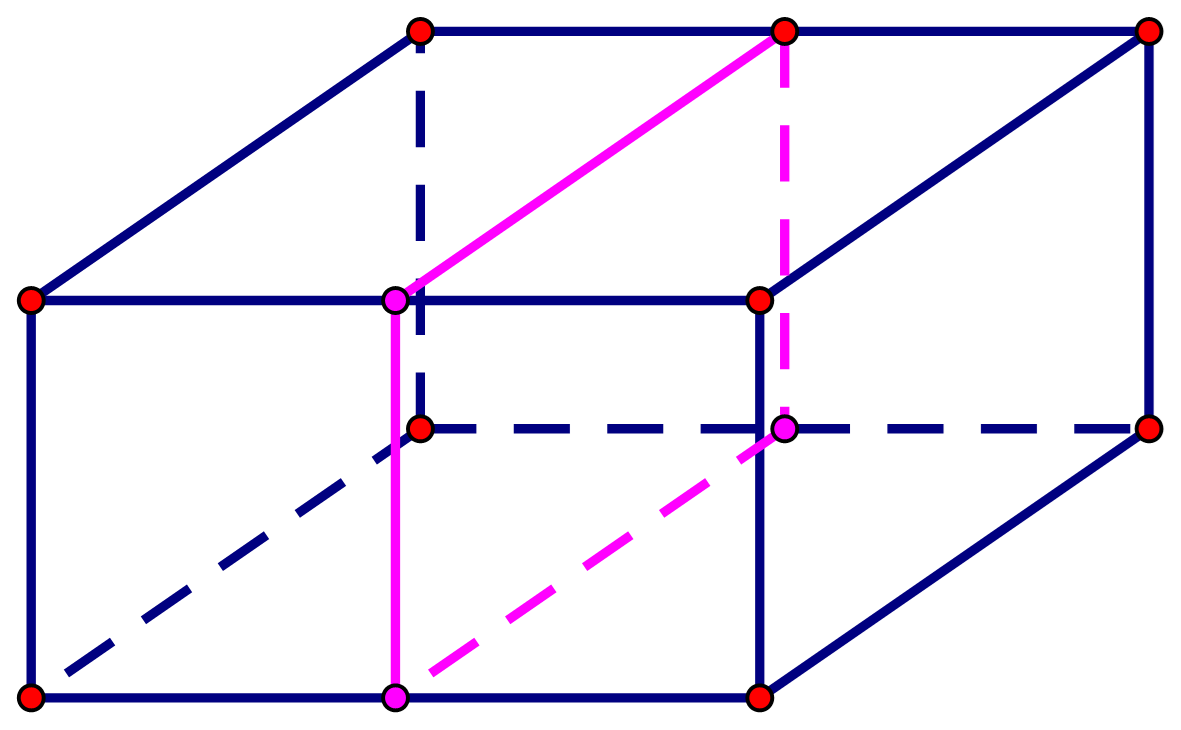
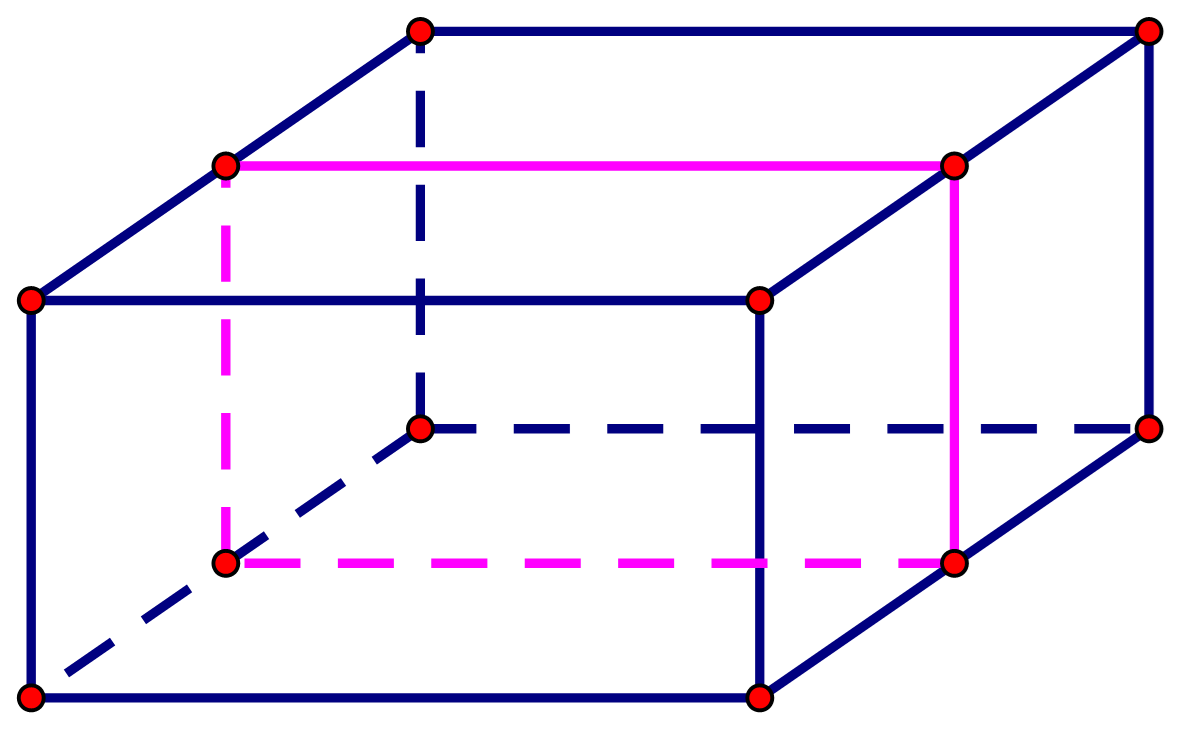
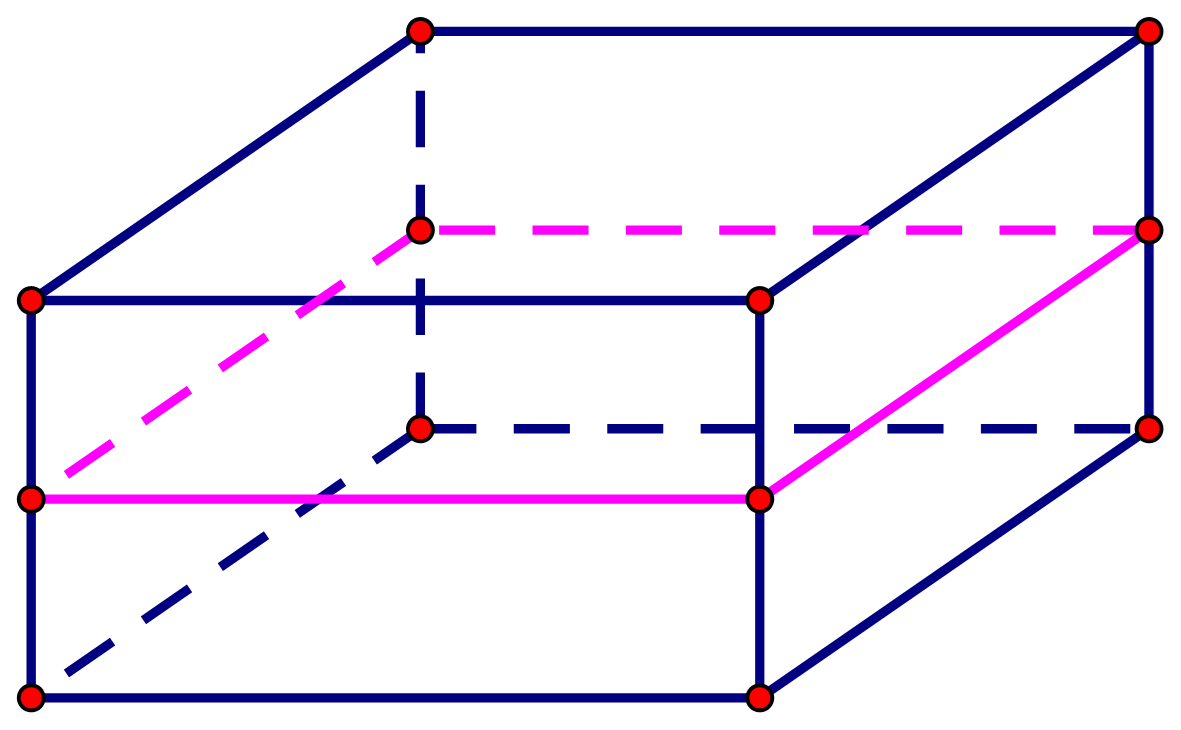
Câu 13:
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
Hình tứ diện có \(4\)đỉnh và \(4\)mặt.
Câu 14:
 Xem đáp án
Xem đáp án
Chọn D
Khối lập phương là đa diện đều loại \(\left\{ {4;3} \right\}\) có 6 mặt.
Mỗi mặt là hình vuông nên số cạnh là \(4.6 = 24\) cạnh.
Nhưng mỗi cạnh là cạnh chung của 2 mặt nên số cạnh của khối lập phương: \(\frac{{24}}{2} = 12\) cạnh.
Có thể áp dụng công thức: Số cạnh \( = \frac{{p.M}}{2}\) hoặc vẽ hình để đếm.
Câu 15:
 Xem đáp án
Xem đáp án
Lời giải
Chọn C
Dựa vào định nghĩa và định lí về khối đa diện đều, khối lập phương thuộc loại \(\left\{ {4\,;\,3} \right\}\).
Câu 16:
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
Ta có tứ diện \(ABCD\) có các cạnh \(AB,AC,AD\)đôi một vuông góc
Nên \(\mathop V\nolimits_{ABCD} = \frac{1}{6}.AB.AC.AD = \frac{1}{6}.3a.5a.8a = 20{a^3}\).
Câu 17:
 Xem đáp án
Xem đáp án
Chọn D
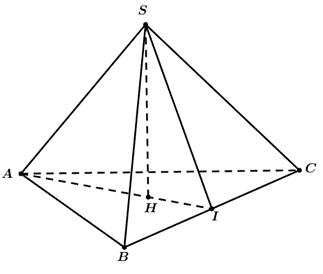
Gọi \[I\] là trung điểm của cạnh \[BC\], \[H\] là trọng tâm của tam giác \[ABC\] ta có: \[SH \bot \left( {ABC} \right)\] và\[SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {S{A^2} - {{\left( {\frac{2}{3}AI} \right)}^2}} = \sqrt {{{\left( {\frac{{a\sqrt {21} }}{6}} \right)}^2} - {{\left( {\frac{2}{3}.\frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{a}{2}.\]
Vậy \[V = \frac{1}{3}.SH.{S_{\Delta ABC}} = \frac{1}{3}.\frac{a}{2}.\frac{1}{2}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{{24}}.\]
Câu 18:
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
\(V = B.h = 7.3 = 21\)
Câu 19:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
Áp dụng công thức tính thể tích khối hộp chữ nhật: \[V = a.b.c\](trong đó: \[a,b,c\] là ba kích thước của hình hộp chữ nhật)
Nên: \[V = 3.4.7 = 84c{m^3}\].
Câu 20:
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
Ta có \[f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right) \Rightarrow f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 2\end{array} \right.\].
Từ đó, ta có bảng biến thiên như sau:
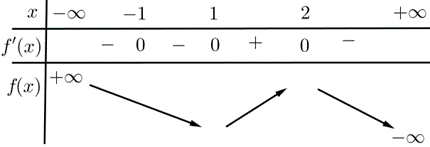
Dựa vào bảng biến thiên thì hàm số \[y = f\left( x \right)\] đồng biến trên \(\left( {1\,;\,2} \right)\).
Câu 21:
 Xem đáp án
Xem đáp án
Chọn A
[phương pháp tự luận]
\[f'\left( x \right) = 3{x^2} - 4mx + 1\].
Hàm số nghịch biến trên \[\left( {1;2} \right)\] khi và chỉ khi \[f'\left( x \right) \le 0,\,\,\forall x \in \left( {1;2} \right)\]
Khi đó \[3{x^2} - 4mx + 1 \le 0 \Leftrightarrow m \ge \frac{{3{x^2} + 1}}{{4x}}\] \[\left( 1 \right)\].
Đặt \[g\left( x \right) = \frac{{3{x^2} + 1}}{{4x}}\]; tập xác định \[D = \left( {1;2} \right)\].
\[g'\left( x \right) = \frac{{12{x^2} - 4}}{{16{x^2}}}\]. \[g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{\sqrt 3 }}{3} & & \left( l \right)\\x = \frac{{ - \sqrt 3 }}{3}\,\,\, & \left( l \right)\end{array} \right.\].
\[\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right) = 1\]; \[\mathop {\lim }\limits_{x \to {2^ - }} g\left( x \right) = \frac{{13}}{8}\].
Ta có bảng biến thiên hàm số \[y = g\left( x \right)\]:

Từ bảng biến thiên, \[\left( 1 \right)\] luôn đúng khi \[m \ge \frac{{13}}{8}\].
[phương pháp trắc nghiệm]
Thay \[m = 2\], lập bảng biến thiên hàm số, ta thấy thỏa mãn yêu cầu bài toán, loại đáp án B,
Thay \[m = \frac{{13}}{8}\], lập bảng biến thiên hàm số, ta thấy thỏa mãn yêu cầu bài toán, loại đáp án
Câu 22:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
Ta có: \(f'\left( x \right) = - {x^2} + 2x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right..\)
Hàm số đã cho có \(2\) điểm cực trị.
Câu 23:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
Yêu cầu bài toán tương đương tìm \[m\] để hàm số đã cho có hai cực trị.
\[y' = \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x + 4\]. Hàm số đã cho có hai cực trị khi và chỉ khi phương trình \(y' = 0\) có hai nghiệm phân biệt, khi đó:
\[\left\{ \begin{array}{l}\Delta ' = {\left( {m - 1} \right)^2} - 4\left( {m - 1} \right) = {m^2} - 6m + 5 > 0 \Leftrightarrow \left[ \begin{array}{l}m < 1\\m > 5\end{array} \right.\\m - 1 \ne 0\end{array} \right.\]\[ \Leftrightarrow \left[ \begin{array}{l}m < 1\\m > 5\end{array} \right.\].
Câu 24:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
TXĐ: \(D = \mathbb{R}\)
\(\begin{array}{*{20}{l}}{y = {x^4} - 2m{x^2} + m + 1}\\{y' = 4{x^3} - 4mx}\\{y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} = m}\end{array}} \right.}\end{array}\)
TH1: \(m \le 0\): Khi đó: \({y_{ct}} = y\left( 0 \right) = {\rm{m}} + 1 = - 1 \Rightarrow m = - 2\)(thỏa mãn).
TH2: \(m > 0\): Khi đó: \({y_{ct}} = y\left( { \pm \sqrt m } \right) = - {m^2} + m + 1 = - 1 \Rightarrow {m^2} - m - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = - 1\;\left( l \right)}\\{m = 2\;\left( {t/m} \right)}\end{array}} \right.\)
Vậy \(S = 0\).
Câu 25:
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
Trên khoảng \(\left( {0;4} \right)\)ta có: \[f'\left( x \right) = \frac{{ - {x^2} + 1}}{{{x^2}}}\], \(f'\left( x \right) = 0 \Leftrightarrow x = 1\).
Bảng biến thiên:
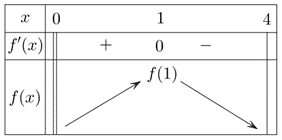
Hàm số đạt giá trị lớn nhất trên khoảng \(\left( {0;4} \right)\) tại \({x_0} = 1\) nên \(P = {x_0} + 2018 = 2019\).
Câu 26:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
Tập xác định \[D = \mathbb{R}\backslash \left\{ { - \frac{1}{2}} \right\}\].
\(y' = \frac{{m + 2}}{{{{\left( {2x + 1} \right)}^2}}}\).
Trường hợp 1: \(y' < 0 \Leftrightarrow m < - 2\). Khi đó \(\mathop {\max y}\limits_{\left[ {1;2} \right]} = y\left( 1 \right) = \frac{{m - 1}}{3} = 3 \Leftrightarrow m = 10\) (loại).
Trường hợp 2: \(y' > 0 \Leftrightarrow m > - 2\). Khi đó \(\mathop {\max y}\limits_{\left[ {1;2} \right]} = y\left( 2 \right) = \frac{{2m - 1}}{5} = 3 \Leftrightarrow m = 8\) (nhận).
Vậy: \(7 < m < 10\).
Câu 27:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
Hàm số xác định khi \[\left\{ \begin{array}{l}2x - {x^2} \ge 0\\x - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 \le x \le 2\\x \ne 1\end{array} \right. \Leftrightarrow x \in \left[ {0;\,2} \right]\backslash \left\{ 1 \right\}\].
Ta có \[\mathop {{\rm{lim}}}\limits_{x \to {1^ - }} y = \mathop {{\rm{lim}}}\limits_{x \to {1^ - }} \frac{{\sqrt {2x - {x^2}} + 1}}{{x - 1}} = - \infty \]; \[\mathop {{\rm{lim}}}\limits_{x \to {1^ + }} y = \mathop {{\rm{lim}}}\limits_{x \to {1^ + }} \frac{{\sqrt {2x - {x^2}} + 1}}{{x - 1}} = + \infty \].
Suy ra \[x = 1\]là đường tiệm cận đứng của đồ thị hàm số.
Câu 28:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
Hàm số có nghĩa khi \(4 - {x^2} > 0 \Leftrightarrow - 2 < x < 2\). TXĐ: \(D = \left( { - 2;2} \right)\)
Hàm số không có tiệm cận ngang.
\[\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{x + 1}}{{\left( {{m^2} + 1} \right)\sqrt {4 - {x^2}} }} = + \infty \]. Suy ra: đường thẳng \(x = 2\) là tiệm cận đứng.
\[\mathop {\lim }\limits_{x \to - {2^ + }} y = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{x + 1}}{{\left( {{m^2} + 1} \right)\sqrt {4 - {x^2}} }} = - \infty \]. Suy ra: đường thẳng \(x = - 2\) là tiệm cận đứng.
Câu 29:
 Xem đáp án
Xem đáp án
Lời giải
Chọn C
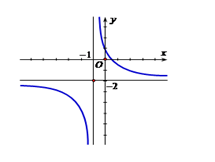
Dễ thấy đồ thị có tiệm cận ngang \(y = - 2 \Rightarrow \) \(a = - 2\).
Đồ thị hàm số cắt \(Oy\) tại điểm \(A\left( {0;1} \right)\) nên \(b = 1\).
Câu 30:
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\] có đồ thị như hình vẽ.
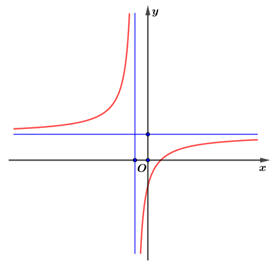
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
Đồ thị hàm số \[y = \frac{{ax + b}}{{cx + d}}\] đi qua \(M\left( {0\,;\,\frac{b}{d}} \right)\), có đường tiệm cận đứng \(x = - \frac{d}{c}\), đường tiệm cận ngang \(y = \frac{a}{c}\).
Quan sát đồ thị thấy:
+ Giao điểm với trục tung nằm phía dưới \(Ox\)nên \(\frac{b}{d} < 0 \Leftrightarrow bd < 0\)\( \Rightarrow \) Loại phương án
+ Đường tiệm cận ngang nằm phía trên \(Ox\)nên \(\frac{a}{c} > 0 \Leftrightarrow ac > 0\)\( \Rightarrow \) Loại phương án
+ Đường tiệm cận đứng nằm bên trái \(Oy\)nên \( - \frac{d}{c} < 0 \Leftrightarrow cd > 0\).
Ta có: \(\left\{ \begin{array}{l}bd < 0\\cd > 0\end{array} \right. \Rightarrow bc < 0\)\( \Rightarrow \) Loại phương án
Kiểm chứng phương án D: \(\left\{ \begin{array}{l}ac > 0\\cd > 0\end{array} \right. \Rightarrow ad > 0\); \(\left\{ \begin{array}{l}ad > 0\\bd < 0\end{array} \right. \Rightarrow ab < 0\).
Lưu ý: Có thể sử dụng giao điểm của đồ thị với trục hoành nằm bên phải \(Oy\)nên \( - \frac{b}{a} > 0 \Leftrightarrow ab < 0\).
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
Ta có \(y = {x^3} - 3{x^2} - 2\backslash \left( {\;\backslash Rightarrow\;\backslash } \right)\)\(y' = 3{x^2} - 6x\); \(y' = 0\backslash \left( {\;\backslash Leftrightarrow\;\backslash } \right)\)\(\left[ {\begin{array}{*{20}{c}}{x = 0 \Rightarrow y = - 2}\\{x = 2 \Rightarrow y = - 6}\end{array}} \right.\).
Bảng biến thiên hàm số \(y = {x^3} - 3{x^2} - 2\):
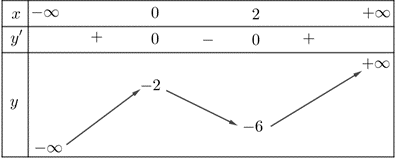
Dựa vào bảng biến thiên ta thấy đường thẳng \(y = 2\) và đồ thị hàm số \(y = {x^3} - 3{x^2} - 2\) có \(1\) điểm chung duy nhất.
Câu 32:
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên sau:
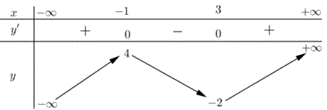
Số nghiệm của phương trình \(f\left( x \right) - 2 = 0\)là
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
\(f\left( x \right) - 2 = 0\;\left( * \right) \Leftrightarrow f\left( x \right) = 2\).
Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\)và đường thẳng \(y = 2\).
Do \(2 \in \left( { - 2;4} \right)\)nên phương trình đã cho có 3 nghiệm phân biệt.
Câu 33:
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
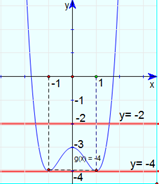
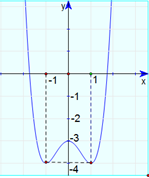
Phương trình \({x^4} - 2{x^2} - 3 = 2m - 4\) có hai nghiệm phân biệt khi chỉ khi đồ thị hàm số \(y = {x^4} - 2{x^2} - 3\) và đường thẳng \(y = 2m - 4\) cắt nhau tại hai điểm phân biệt.
Dựa vào đồ thị hàm số trên, yêu cầu bài toán thỏa mãn khi \(\left[ \begin{array}{l}2m - 4 = - 4\\2m - 4 > - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m > \frac{1}{2}\end{array} \right.\).
Câu 34:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
Số cạnh đáy của khối lăng trụ là: \(5.2 = 10\).
Số cạnh bên của lăng trụ là: \(5\).
Do đó số cạnh của khối lăng trụ ngũ giác là \(15\).
Câu 35:
 Xem đáp án
Xem đáp án
Lời giải
Chọn C
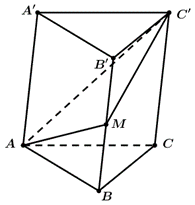
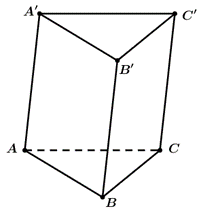
Mặt phẳng \(\left( {AMC'} \right)\) chia khối lăng trụ đã cho thành hai khối chóp tứ giác là khối \(A.MBCC'\) và \(C'.AA'B'M\).
Câu 36:
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
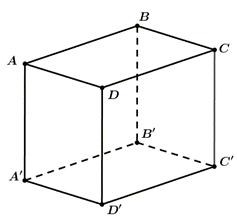
Gọi hình lăng trụ đứng đã cho là \(ABCD.A'B'C'D'\) với đáy là hình thoi \(ABCD\).
Các mặt phẳng đối xứng của nó bao gồm:
- mặt phẳng trung trực của các cạnh bên
- mặt phẳng \(\left( {ACC'A'} \right)\)
- mặt phẳng \(\left( {BDD'B'} \right)\).Câu 37:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
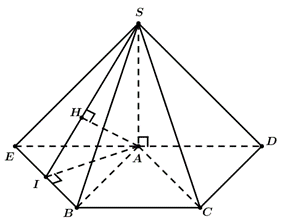
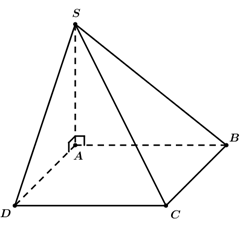
Dựng điểm \(E\) sao cho \(ACBE\) là hình bình hành.
Khi đó: \(AC//EB \Rightarrow AC//\left( {SBE} \right) \Rightarrow d\left( {AC,SB} \right) = d\left( {AC,\left( {SBE} \right)} \right) = d\left( {A,\left( {SBE} \right)} \right)\).
Kẻ \(AI \bot EB\left( {I \in AB} \right)\), kẻ \(AH \bot SI\left( {H \in SI} \right) \Rightarrow d\left( {A,\left( {SEB} \right)} \right) = AH = a\).
Tam giác \(A\) vuông tại tại \(A\).
Ta có \(\frac{1}{{A{I^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{E^2}}} = \frac{1}{{4{a^2}}} + \frac{1}{{4{a^2}}} = \frac{1}{{2{a^2}}}\).
Xét \(\Delta SAI\), ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{I^2}}} \Leftrightarrow \frac{1}{{{a^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{2{a^2}}} \Leftrightarrow \frac{1}{{S{A^2}}} = \frac{1}{{2{a^2}}} \Rightarrow SA = a\sqrt 2 \).
Vậy thể tích của tích khối chóp \(S.ABCD\) là \({V_{S.ABCD}} = \frac{1}{3}.SA.{S_{ABCD}} = \frac{1}{3}.a\sqrt 2 .4{a^2} = \frac{{4\sqrt 2 {a^3}}}{3}\).
Câu 38:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
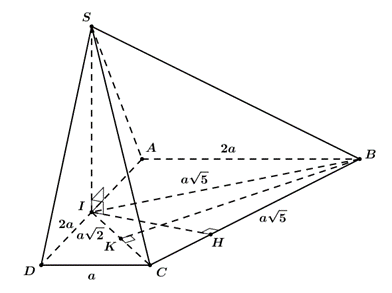
Do \[\left( {SBI} \right) \bot \left( {ABCD} \right)\] và \[\left( {SCI} \right) \bot \left( {ABCD} \right)\] nên \[SI \bot \left( {ABCD} \right)\].
Ta có \[IB = \sqrt {A{B^2} + A{I^2}} = a\sqrt 5 \], \[CI = \sqrt {C{D^2} + D{I^2}} = a\sqrt 2 \], suy ra tam giác \[BCI\] cân tại \[B\].
Gọi \[K\] là trung điểm của \[CI\], \[BK = \sqrt {B{C^2} - C{K^2}} = \sqrt {{{\left( {a\sqrt 5 } \right)}^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{3a\sqrt 2 }}{2}\], \[{S_{\Delta BCI}} = \frac{1}{2}BK.CI = \frac{{3{a^2}}}{2}\].
Kẻ \[IH \bot BC \Rightarrow BC \bot SH\] nên góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và \[\left( {ABCD} \right)\] là góc \[\widehat {SHI}\].
Mà \[{S_{\Delta BCI}} = \frac{1}{2}IH.BC \Rightarrow IH = \frac{{2{S_{\Delta BCI}}}}{{BC}} = \frac{{3a}}{{\sqrt 5 }}\], \[SI = IH.\tan 60^\circ = \frac{{3a}}{{\sqrt 5 }}.\sqrt 3 = \frac{{3a\sqrt {15} }}{5}\].
Vậy \[{V_{S.ABCD}} = \frac{1}{3}SI.{S_{ABCD}} = \frac{1}{3}\frac{{3a\sqrt {15} }}{5}\frac{{a + 2a}}{2}.2a = \frac{{3{a^3}\sqrt {15} }}{5}\].
Câu 39:
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:

Hàm số \(y = 3f\left( {x + 3} \right) - {x^3} + 12x\) nghịch biến trên khoảng nào sau đây?
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
Ta có \(y' = 3f'\left( {x + 3} \right) - 3{x^2} + 12 = 3\left[ {f'\left( {x + 3} \right) + \left( {4 - {x^2}} \right)} \right]\)
Từ bảng xét dấu của \(f'\left( x \right)\) ta có \(f'\left( {x + 3} \right) < 0 \Leftrightarrow \left[ \begin{array}{l} - 1 < x + 3 < 1\\5 < x + 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 4 < x < - 2\\x > 2\end{array} \right.\);
\(f'\left( {x + 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 4\\x = \pm 2\end{array} \right.\).
Suy ra bảng xét dấu \(y'\) như sau
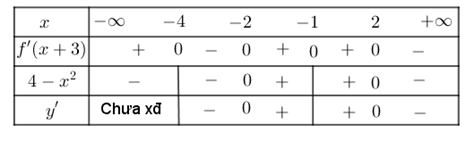
Vậy hàm số \(y = 3f\left( {x + 3} \right) - {x^3} + 12x\) nghịch biến trên khoảng \(\left( {2; + \infty } \right)\) và \(\left( { - 4; - 2} \right)\).
Câu 40:
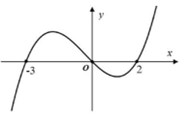
 Xem đáp án
Xem đáp án
Lời giải
Chọn D
Ta có: \(g'\left( x \right) = 2xf'\left( {{x^2} - 2} \right) - 6f'\left( {2 - 2x} \right) = k\left( x \right) + q\left( x \right)\)
Đặt
\[k\left( x \right) = 2xf'\left( {{x^2} - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\\{x^2} - 2 = - 3\\{x^2} - 2 = 0\\{x^2} - 2 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \\x = \pm 2\end{array} \right.\]
Đặt
\(q\left( x \right) = - 6f'\left( {2 - 2x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2 - 2x = - 3\\2 - 2x = 0\\2 - 2x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{5}{2}\\x = 1\\x = 0\end{array} \right.\)
Ta có bảng xét dấu
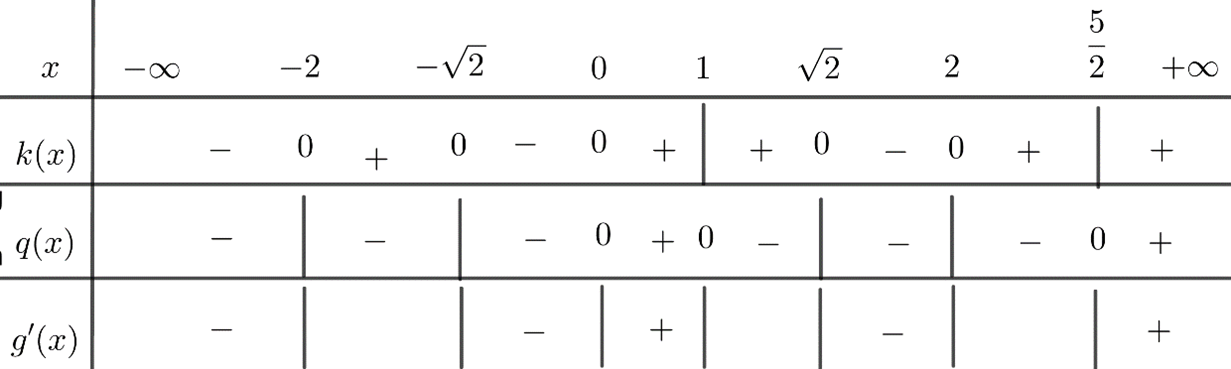
Suy ra hàm số \(g\left( x \right) = f\left( {{x^2} - 2} \right) + 3f\left( {2 - 2x} \right) + 1\) nghịch biến trên khoảng \(\left( { - 1;0} \right)\).
Câu 41:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
Để hàm số \(y = \frac{{mx - 2}}{{ - 2x + m}}\) nghịch biến trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\) khi và chỉ khi
\[\left\{ \begin{array}{l}\frac{m}{2} \le \frac{1}{2}\\{m^2} - 4 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 1\\ - 2 < m < 2\end{array} \right. \Leftrightarrow - 2 < m \le 1\].
Câu 42:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
\[y = \frac{1}{3}{x^3} - \left( {2m - 1} \right){x^2} + \left( {{m^2} - m + 7} \right)x + m - 5\]\[ \Rightarrow y' = {x^2} - 2\left( {2m - 1} \right)x + {m^2} - m + 7\].
+) Hàm số có hai điểm cực trị là độ dài hai cạnh của một tam giác vuông thì \[y'\] có 2 nghiệm dương phân biệt \( \Leftrightarrow \)\[\left\{ \begin{array}{l}\Delta ' = {\left( {2m - 1} \right)^2} - \left( {{m^2} - m - 7} \right) > 0\\2m - 1 > 0\\{m^2} - m + 7 > 0\end{array} \right.\](*).
+) Khi đó, gọi \[{x_1}\], \[{x_2}\] là 2 điểm cực trị của hàm số thì \[{x_1}\], \[{x_2}\] là hai nghiệm của \[y'\] \[ \Rightarrow \left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {2m - 1} \right)\\{x_1}.{x_2} = {m^2} - m + 7\end{array} \right.\].
Theo giả thiết ta có \[x_1^2 + x_2^2 = 74\]\[ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 74\]\[ \Leftrightarrow 4{\left( {2m - 1} \right)^2} - 2.\left( {{m^2} - m + 7} \right) = 74\]\[ \Leftrightarrow 14{m^2} - 14m - 84 = 0\]\[ \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = - 2\end{array} \right.\].
Thử vào \[\left( * \right) \Rightarrow m = 3\].
Câu 43:
 Xem đáp án
Xem đáp án
Lời giải
Chọn C
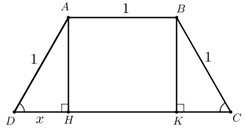
Kẻ \(AH \bot CD,BK \bot CD \Rightarrow ABKH\) là hình chữ nhật \( \Rightarrow AB = HK = 1\left( m \right).\)
Đặt \(DH = x.\) Khi đó \(AH = \sqrt {1 - {x^2}} \left( {0 < x < 1} \right).\)
Vì \(ABCD\) là hình thang cân nên \(\Delta ADH = \Delta BCK\) (cạnh huyền – góc nhọn)
\( \Rightarrow DH = CK = x \Rightarrow CD = DH + HK + CK = 2x + 1.\)
Ta có \({S_{ABCD}} = \frac{{\left( {AB + CD} \right).AH}}{2} = \frac{{\left( {1 + 2x + 1} \right)\sqrt {1 - {x^2}} }}{2} = \left( {x + 1} \right)\sqrt {1 - {x^2}} .\)
Xét hàm số \(f\left( x \right) = \left( {x + 1} \right)\sqrt {1 - {x^2}} \left( {0 < x < 1} \right),\) ta có
\(f'\left( x \right) = \sqrt {1 - {x^2}} - \frac{{2x\left( {x + 1} \right)}}{{2\sqrt {1 - {x^2}} }} = \frac{{ - 2{x^2} - x + 1}}{{\sqrt {1 - {x^2}} }},\) \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{1}{2}\left( n \right)}\\{x = - 1\left( l \right)}\end{array}} \right..\)
Bảng biến thiên:
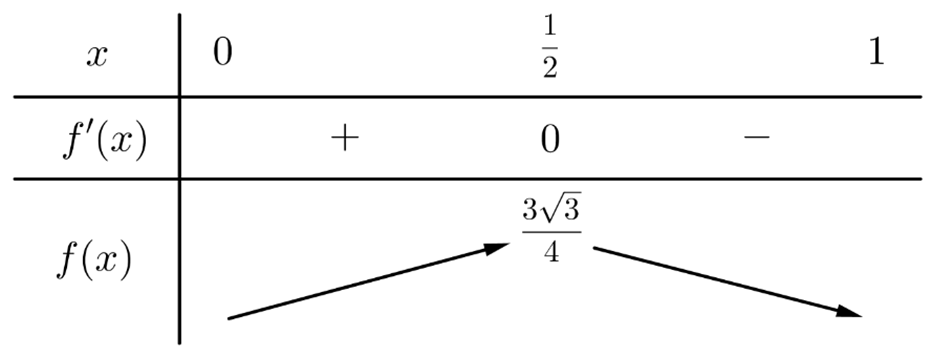
Dựa vào bảng biến thiên, ta thấy \(f\left( x \right) \le f\left( {\frac{1}{2}} \right) = \frac{{3\sqrt 3 }}{4}.\)
Vậy diện tích lớn nhất của hình thang \(ABCD\) là \(\frac{{3\sqrt 3 }}{4}\left( {{m^2}} \right).\)
Câu 44:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có bảng biến thiên như sau
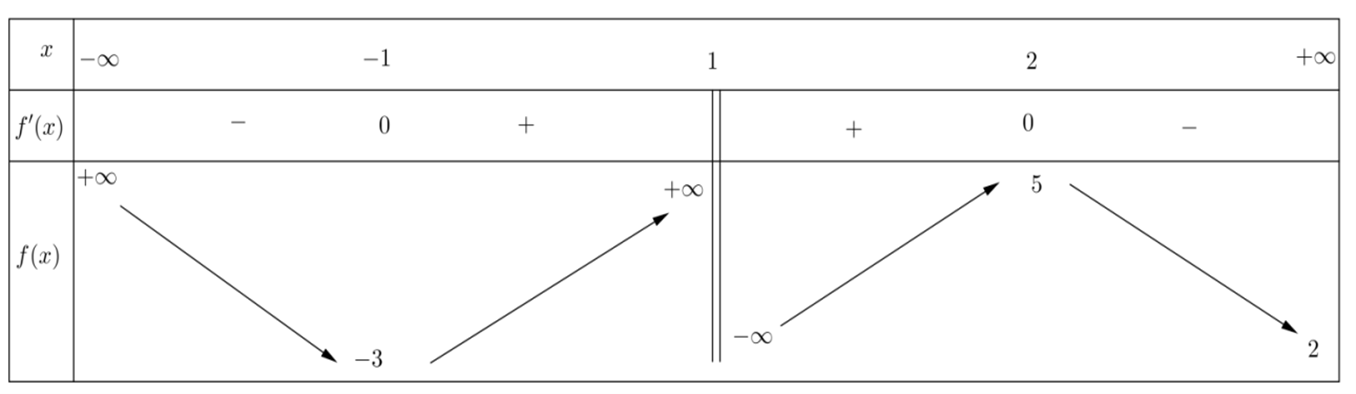
Số đường tiệm cận đứng của đồ thị hàm số \(y = g\left( x \right) = \frac{{2020}}{{f\left( x \right) - 3}}\).
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên ta có:
Phương trình \(f\left( x \right) - 3 = 0\) \( \Leftrightarrow f\left( x \right) = 3 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = a \in \left( { - \infty ; - 1} \right)}\\{x = b \in \left( { - 1;1} \right)}\\{x = c \in \left( {1;2} \right)}\\{x = d \in \left( {2; + \infty } \right)}\end{array}} \right.\).
\(\mathop {lim}\limits_{x \to {a^ + }} g\left( x \right) = \mathop {lim}\limits_{x \to {a^ + }} \frac{{2020}}{{f\left( x \right) - 3}} = - \infty \Rightarrow \) đường thẳng \(x = a\) là đường tiệm cận đứng. \(\mathop {lim}\limits_{x \to {b^ + }} g\left( x \right) = \mathop {lim}\limits_{x \to {b^ + }} \frac{{2020}}{{f\left( x \right) - 3}} = + \infty \) \( \Rightarrow \) đường thẳng \(x = b\) là đường tiệm cận đứng.
\(\mathop {lim}\limits_{x \to {c^ + }} g\left( x \right) = \mathop {lim}\limits_{x \to {c^ + }} \frac{{2020}}{{f\left( x \right) - 3}} = + \infty {\rm{\;}} \Rightarrow \)đ ường thẳng \(x = c\) là đường tiệm cận đứng.
\(\mathop {lim}\limits_{x \to {d^ + }} g\left( x \right) = \mathop {lim}\limits_{x \to {d^ + }} \frac{{2020}}{{f\left( x \right) - 3}} = - \infty \) \( \Rightarrow \) đường thẳng \(x = d\) là đường tiệm cận đứng.
Vậy đồ thị hàm số \(y = g\left( x \right) = \frac{{2020}}{{f\left( x \right) - 3}}\) có 4 đường tiệm cận đứng.
Câu 45:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
Cách 1:
Xét phương trình hoành độ giao điểm của đường thẳng \(\left( d \right)\) và đường cong \(\left( C \right)\): \({x^3} - 3{x^2} + 1 = mx - m - 1\) \( \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2x - 2 - m} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{{x^2} - 2x - 2 - m = 0\left( * \right)}\end{array}} \right.\).
\(\left( d \right)\) cắt \(\left( C \right)\) tại \(3\) điểm phân biệt \(A\), \(B\), \(C\) \( \Leftrightarrow \) \(\left( * \right)\) có hai nghiệm phân biệt khác \(1\).
\(\left( * \right) \Leftrightarrow {\left( {x - 1} \right)^2} = m + 3\) có hai nghiệm phân biệt khác \(1\) khi và chỉ khi \(m > - 3\).
Khi đó \(\left( * \right)\) có hai nghiệm \({x_1} = 1 - \sqrt {m + 3} \), \({x_2} = 1 + \sqrt {m + 3} \) thỏa \({x_1} < 1 < {x_2}\).
Không mất tính tổng quát, gọi \(A\left( {1 - \sqrt {m + 3} ; - m\sqrt {m + 3} - 1} \right)\), \(B\left( {1; - 1} \right)\), \(C\left( {1 + \sqrt {m + 3} ;m\sqrt {m + 3} - 1} \right)\).
Tam giác \(AOC\) cân tại \(O\) \( \Leftrightarrow OA = OC \Leftrightarrow O{A^2} = O{C^2}\)
\( \Leftrightarrow {\left( {1 - \sqrt {m + 3} } \right)^2} + {\left( { - m\sqrt {m + 3} - 1} \right)^2} = {\left( {1 + \sqrt {m + 3} } \right)^2} + {\left( {m\sqrt {m + 3} - 1} \right)^2}\)
\( \Leftrightarrow 4\sqrt {m + 3} - 4m\sqrt {m + 3} = 0 \Leftrightarrow 4\left( {m - 1} \right)\sqrt {m + 3} = 0 \Leftrightarrow m = 1\).
Với \(m = 1\) thỏa mãn điều kiện tồn tại các điểm \(A\), \(B\), \(C\) và khi đó đường thẳng \(\left( d \right):y = x - 2\) không đi qua gốc tọa độ \(O\) nên \(A\), \(O\), \(C\) tạo thành tam giác cân. Vậy \(m = 1\) là giá trị cần tìm.
Cách 2:
Xét phương trình hoành độ giao điểm của đường thẳng \(\left( d \right)\) và đường cong \(\left( C \right)\): \({x^3} - 3{x^2} + 1 = mx - m - 1\) \( \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2x - 2 - m} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{{x^2} - 2x - 2 - m = 0\left( * \right)}\end{array}} \right.\).
\(\left( d \right)\) cắt \(\left( C \right)\) tại \(3\) điểm phân biệt \(A\), \(B\), \(C\) \( \Leftrightarrow \) \(\left( * \right)\) có hai nghiệm phân biệt khác \(1\).
\(\left( * \right) \Leftrightarrow {\left( {x - 1} \right)^2} = m + 3\) có hai nghiệm phân biệt \({x_1}\),\({x_2}\) khác \(1\) khi và chỉ khi \(m > - 3\).
Xét \({x^2} - 2x - 2 - m = 0\,\)\(\left( * \right)\)
Theo Viet:\(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2}\\{{x_1}{x_2} = - m - 2}\end{array}} \right.\)
Khi đó:\(A\left( {{x_1};m{x_1} - m - 1} \right)\),\(B\left( {{x_2};m{x_2} - m - 1} \right)\).
Cần có:\(O{A^2} = O{B^2}\)
\( \Leftrightarrow x_1^2 + {\left( {m{x_1} - m - 1} \right)^2} = x_2^2 + {\left( {m{x_2} - m - 1} \right)^2}\)
\( \Leftrightarrow \left( {{x_1} - {x_2}} \right)\left[ {\left( {{x_1} + {x_2}} \right) + m\left[ {m\left( {{x_1} + {x_2}} \right) - 2m - 2} \right]} \right] = 0\)
\( \Leftrightarrow \left[ {\left( {{x_1} + {x_2}} \right) + m\left[ {m\left( {{x_1} + {x_2}} \right) - 2m - 2} \right]} \right] = 0\)
\( \Leftrightarrow 2 + m\left( {2m - 2m - 2} \right) = 0 \Leftrightarrow m = 1\).
Câu 46:
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau
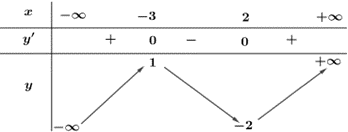
Phương trình \(f\left( {f\left( x \right)} \right) = 0\)có nhiều nhất bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Lời giải
Chọn C
Ta có: \(f\left( {f\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = {x_1}{\rm{ }}\left( {{x_1} < - 3} \right){\rm{ }}\\f\left( x \right) = {x_2}{\rm{ }}\left( { - 3 < {x_2} < 2} \right)\\f\left( x \right) = {x_3}{\rm{ }}\left( {{x_3} > 2} \right){\rm{ }}\end{array} \right.\).
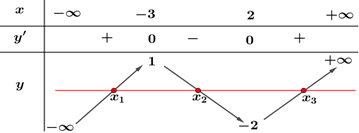
Dựa vào bảng biến thiên
+ Trường hợp 1: \(f\left( x \right) = {x_1}{\rm{ }}\left( {{x_1} < - 3} \right)\)có 1 nghiệm.
+ Trường hợp 2: \(f\left( x \right) = {x_2}{\rm{ }}\left( { - 3 < {x_2} < 2} \right)\)có nhiều nhất 3 nghiệm.
+ Trường hợp 3: \(f\left( x \right) = {x_3}{\rm{ }}\left( {{x_3} > 2} \right)\)có 1 nghiệm.
Vậy phương trình \(f\left( {f\left( x \right)} \right) = 0\)có nhiều nhất 5 nghiệm.
Câu 47:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
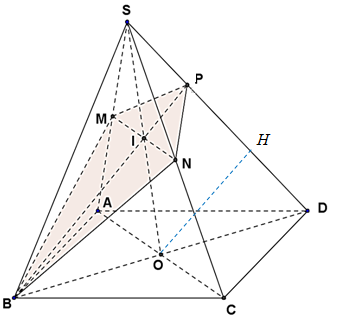
Ta có \(M,N\)là trung điểm của \(SA,SC\)nên \(\frac{{SM}}{{SA}} = \frac{{SN}}{{SC}} = \frac{1}{2}\).
Cách 1: Áp dụng định lý Menelaus cho \(\Delta SOD\)ta có :\[\frac{{PS}}{{PD}} \cdot \frac{{BD}}{{BO}} \cdot \frac{{IO}}{{IS}} = 1 \Rightarrow \frac{{PS}}{{PD}} \cdot 2 \cdot 1 = 1 \Rightarrow \frac{{PS}}{{PD}} = \frac{1}{2} \Rightarrow \frac{{SP}}{{SD}} = \frac{1}{3}\].
Cách 2: Kẻ \(OH//BP\), ta có \(O\)là trung điểm của \(BD\)nên \(H\)là trung điểm của \(PD\).
Ta có \(OH//IP\)mà \(I\)là trung điểm của \(SO\)nên \(P\)là trung điểm của \(SH\).
Suy ra \(SP = PH = HD\)\[ \Rightarrow \frac{{SP}}{{SD}} = \frac{1}{3}\].
Theo công thức tỉ số thể tích ta có : \(\frac{{{V_{S.BMPN}}}}{{{V_{S.ABCD}}}} = \frac{{2{V_{S.BMP}}}}{{2{V_{S.BAD}}}} = \frac{{SM}}{{SA}} \cdot \frac{{SP}}{{SD}} = \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6}.\)Câu 48:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
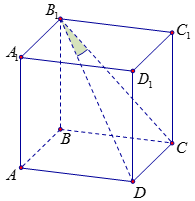
Ta có \(DC \bot \left( {BC{C_1}{B_1}} \right)\) suy ra hình chiếu của \(D{B_1}\) lên \(\left( {BC{C_1}{B_1}} \right)\) là \(C{B_1}\)
\( \Rightarrow \widehat {\left( {D{B_1},\left( {BC{C_1}{B_1}} \right)} \right)} = \widehat {\left( {D{B_1},C{B_1}} \right)} = \widehat {D{B_1}C} = 30^\circ \)
Xét \(\Delta D{B_1}C\) vuông ở \(C\) có \(\tan \widehat {D{B_1}C} = \frac{{DC}}{{{B_1}C}} \Leftrightarrow \tan 30^\circ = \frac{a}{{{B_1}C}} \Rightarrow {B_1}C = a\sqrt 3 \)
Xét \(\Delta {B_1}BC\) vuông ở \(B\) có \(B{B_1} = \sqrt {{B_1}{C^2} - B{C^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \)
Thể tích khối hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\) là \(V = B{B_1}.{S_{ABCD}} = a\sqrt 2 .{a^2} = {a^3}\sqrt 2 \).
Câu 49:
 Xem đáp án
Xem đáp án
Lời giải
Chọn B
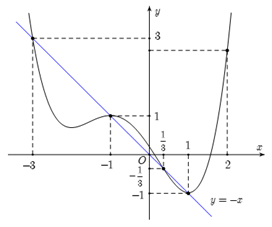
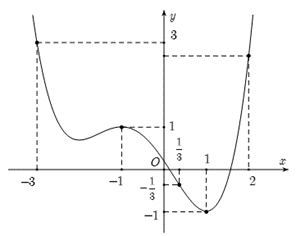
Ta có \(g\left( x \right) = 2f\left( {\frac{{5\sin x - 1}}{2}} \right) + {\left( {\frac{{5\sin x - 1}}{2}} \right)^2} + 3\)
\[g'\left( x \right) = \frac{{5\cos x}}{2}\left[ {2f'\left( {\frac{{5\sin x - 1}}{2}} \right) + 2.\left( {\frac{{5\sin x - 1}}{2}} \right)} \right] = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{2f'\left( {\frac{{5\sin x - 1}}{2}} \right) + 2.\left( {\frac{{5\sin x - 1}}{2}} \right) = 0}\end{array}} \right.\]
Đặt \[t = \frac{{5\sin x - 1}}{2}\]vì \(x \in \left( {0\,;\,2\pi } \right) \Rightarrow t \in \left[ { - 3;2} \right]\)
Khi đó: \[2f'\left( {\frac{{5\sin x - 1}}{2}} \right) + 2.\left( {\frac{{5\sin x - 1}}{2}} \right) = 0\]thành \[f'\left( t \right) = - t \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{t = 1}\\{t = \frac{1}{3}\,}\end{array}}\\{\begin{array}{*{20}{c}}{t = - 1}\\{t = - 3}\end{array}}\end{array}} \right.\]
Với \(t = 1 \Rightarrow \frac{{5\sin x - 1}}{2} = 1 \Leftrightarrow \sin x = \frac{3}{5} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = {\alpha _1} \in \left( {0\,;\,2\pi } \right)}\\{x = {\alpha _2} \in \left( {0\,;\,2\pi } \right)}\end{array}} \right.\).
Với \(t = \frac{1}{3}\, \Rightarrow \frac{{5\sin x - 1}}{2} = \frac{1}{3} \Leftrightarrow \sin x = \,\frac{1}{3} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = {\alpha _3} \in \left( {0\,;\,2\pi } \right)}\\{x = {\alpha _4} \in \left( {0\,;\,2\pi } \right)}\end{array}} \right.\).
Với \(t = - 1 \Rightarrow \frac{{5\sin x - 1}}{2} = - 1 \Leftrightarrow \sin x = - \frac{1}{5} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = {\alpha _5} \in \left( {0\,;\,2\pi } \right)}\\{x = {\alpha _6} \in \left( {0\,;\,2\pi } \right)}\end{array}} \right.\).
Với \(t = - 3 \Rightarrow \frac{{5\sin x - 1}}{2} = - 3 \Leftrightarrow \sin x = - 1 \Leftrightarrow x = \frac{{3\pi }}{2} \in \left( {0\,;\,2\pi } \right)\).
\(\cos x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} \in \left( {0\,;\,2\pi } \right)}\\{x = \frac{{3\pi }}{2} \in \left( {0\,;\,2\pi } \right)}\end{array}} \right.\).
Vì \[x = \frac{{3\pi }}{2}\]là nghiệm kép nên không là điểm cực trị của hàm số \(y = g\left( x \right)\).
Vậy hàm số \(y = g\left( x \right)\)có \[7\]điểm cực trị trên khoảng \(\left( {0\,;\,2\pi } \right)\).
Câu 50:
 Xem đáp án
Xem đáp án
Lời giải
Chọn C
Ta xét \(f\left( x \right) = {x^4} - 2{x^3} + m\) liên tục trên đoạn \(\left[ {0;1} \right]\), \(f'\left( x \right) = 4{x^3} - 6{x^2}\).
\(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0 \in \left[ {0;1} \right]}\\{x = \frac{3}{2} \notin \left[ {0;1} \right]}\end{array}} \right.\).
\(f\left( 0 \right) = m;f\left( 1 \right) = m - 1\).
Ta xét các trường hợp sau:
-Nếu \(m \le 0\) thì \(\mathop {max}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = 1 - m;\mathop {min}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = - m\).
Khi đó: \(\mathop {max}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| + 2\mathop {min}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = 10 \Leftrightarrow \left( {1 - m} \right) + 2\left( { - m} \right) = 10 \Leftrightarrow m = - 3\) (thỏa điều kiện).
-Nếu \(m \ge 1\) thì \(\mathop {max}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = m;\mathop {min}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = m - 1\).
Khi đó: \(\mathop {max}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| + 2\mathop {min}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = 10 \Leftrightarrow m + 2\left( {m - 1} \right) = 10 \Leftrightarrow m = 4\) (thỏa điều kiện).
-Nếu \(\frac{1}{2} \le m < 1\) thì \(\mathop {max}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = m;\mathop {min}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = 0\).
Khi đó: \(\mathop {max}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| + 2\mathop {min}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = 10 \Leftrightarrow m = 10\) (không thỏa điều kiện).
-Nếu \(0 < m < \frac{1}{2}\) thì \(\mathop {max}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = 1 - m;\mathop {min}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = 0\).
Khi đó: \(\mathop {max}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| + 2\mathop {min}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = 10 \Leftrightarrow 1 - m = 10 \Leftrightarrow m = - 9\) (không thỏa điều kiện).
Do đó có hai giá trị \(m = - 3\) và \(m = 4\) thỏa mãn yêu cầu bài toán.
Vậy tổng tất cả các giá trị của \(m\) sao cho \(\mathop {max}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| + 2\mathop {min}\limits_{\left[ {0;1} \right]} \left| {f\left( x \right)} \right| = 10\) là \(1\).