Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên sau:
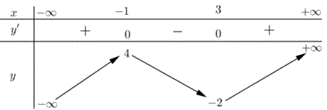
Số nghiệm của phương trình \(f\left( x \right) - 2 = 0\)là
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn A
\(f\left( x \right) - 2 = 0\;\left( * \right) \Leftrightarrow f\left( x \right) = 2\).
Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\)và đường thẳng \(y = 2\).
Do \(2 \in \left( { - 2;4} \right)\)nên phương trình đã cho có 3 nghiệm phân biệt.
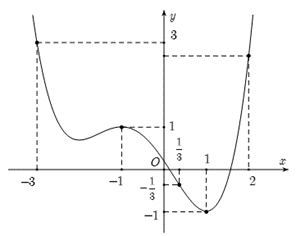
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:

Hàm số \(y = 3f\left( {x + 3} \right) - {x^3} + 12x\) nghịch biến trên khoảng nào sau đây?