Giải bởi Vietjack
Lời giải
Chọn B
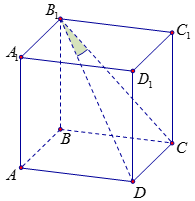
Ta có \(DC \bot \left( {BC{C_1}{B_1}} \right)\) suy ra hình chiếu của \(D{B_1}\) lên \(\left( {BC{C_1}{B_1}} \right)\) là \(C{B_1}\)
\( \Rightarrow \widehat {\left( {D{B_1},\left( {BC{C_1}{B_1}} \right)} \right)} = \widehat {\left( {D{B_1},C{B_1}} \right)} = \widehat {D{B_1}C} = 30^\circ \)
Xét \(\Delta D{B_1}C\) vuông ở \(C\) có \(\tan \widehat {D{B_1}C} = \frac{{DC}}{{{B_1}C}} \Leftrightarrow \tan 30^\circ = \frac{a}{{{B_1}C}} \Rightarrow {B_1}C = a\sqrt 3 \)
Xét \(\Delta {B_1}BC\) vuông ở \(B\) có \(B{B_1} = \sqrt {{B_1}{C^2} - B{C^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \)
Thể tích khối hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\) là \(V = B{B_1}.{S_{ABCD}} = a\sqrt 2 .{a^2} = {a^3}\sqrt 2 \).
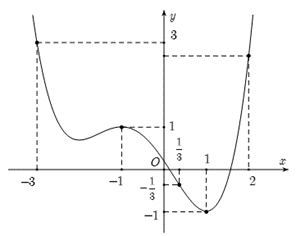
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:
Hàm số \(y = 3f\left( {x + 3} \right) - {x^3} + 12x\) nghịch biến trên khoảng nào sau đây?
