Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án (Đề 4)
-
4333 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Câu 2:
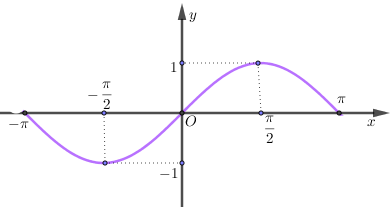
Trên khoảng \(\left( { - \pi \,;\,\pi } \right)\) đồ thị hàm số \(y = \sin x\) được cho như hình vẽ:
 Xem đáp án
Xem đáp án
Câu 3:
 Xem đáp án
Xem đáp án
Câu 4:
 Xem đáp án
Xem đáp án
Câu 5:
 Xem đáp án
Xem đáp án
Câu 6:
 Xem đáp án
Xem đáp án
Câu 7:
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ:
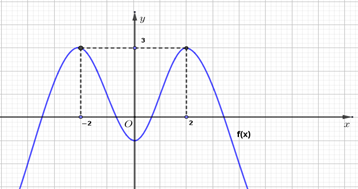
 Xem đáp án
Xem đáp án
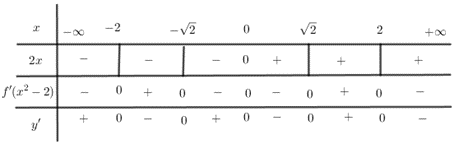
Câu 8:
 Xem đáp án
Xem đáp án

Câu 9:
 Xem đáp án
Xem đáp án

Câu 10:
 Xem đáp án
Xem đáp án
Câu 11:
 Xem đáp án
Xem đáp án
Câu 12:
 Xem đáp án
Xem đáp án
Câu 13:
 Xem đáp án
Xem đáp án
Câu 14:
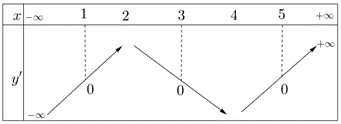
 Xem đáp án
Xem đáp án
Câu 15:
 Xem đáp án
Xem đáp án
Câu 16:
 Xem đáp án
Xem đáp án
Câu 17:
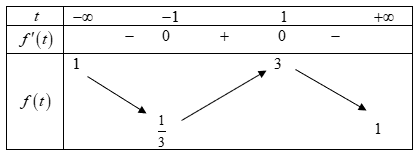
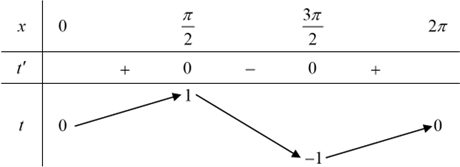
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
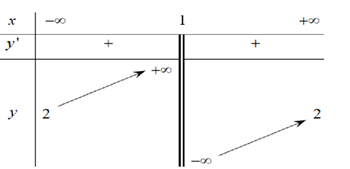
 Xem đáp án
Xem đáp án
Câu 18:
 Xem đáp án
Xem đáp án
Câu 19:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
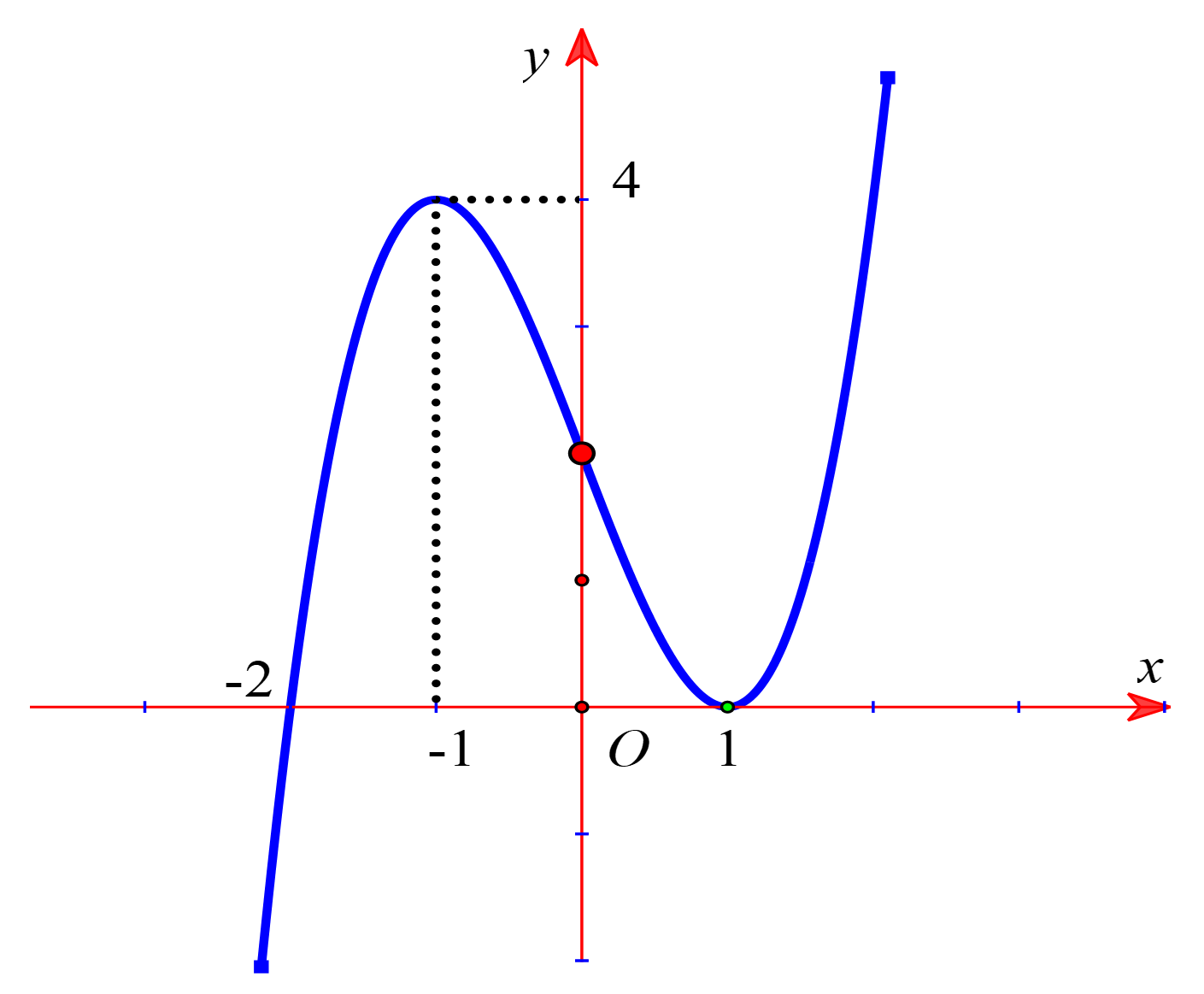
 Xem đáp án
Xem đáp án
Câu 20:
 Xem đáp án
Xem đáp án
Câu 21:
 Xem đáp án
Xem đáp án
Câu 22:
 Xem đáp án
Xem đáp án
Câu 23:
 Xem đáp án
Xem đáp án
Câu 24:
 Xem đáp án
Xem đáp án
Câu 25:
 Xem đáp án
Xem đáp án
Câu 26:
 Xem đáp án
Xem đáp án
Câu 27:
 Xem đáp án
Xem đáp án
Câu 28:
 Xem đáp án
Xem đáp án
Câu 29:
 Xem đáp án
Xem đáp án
Câu 30:
 Xem đáp án
Xem đáp án
Câu 31:
 Xem đáp án
Xem đáp án
Câu 32:
Đồ thị dưới đây của hàm số nào?
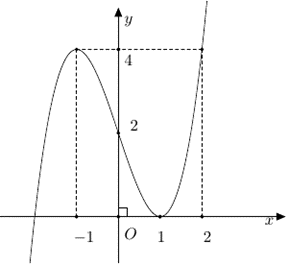
 Xem đáp án
Xem đáp án
Câu 33:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ sau:
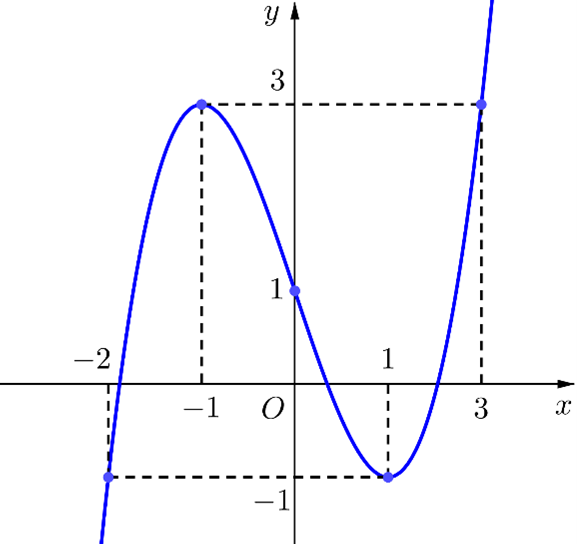
 Xem đáp án
Xem đáp án
Câu 34:
 Xem đáp án
Xem đáp án
Câu 35:
 Xem đáp án
Xem đáp án
Câu 36:
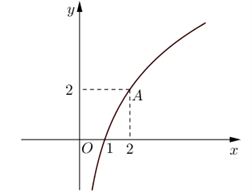
 Xem đáp án
Xem đáp án
Câu 37:
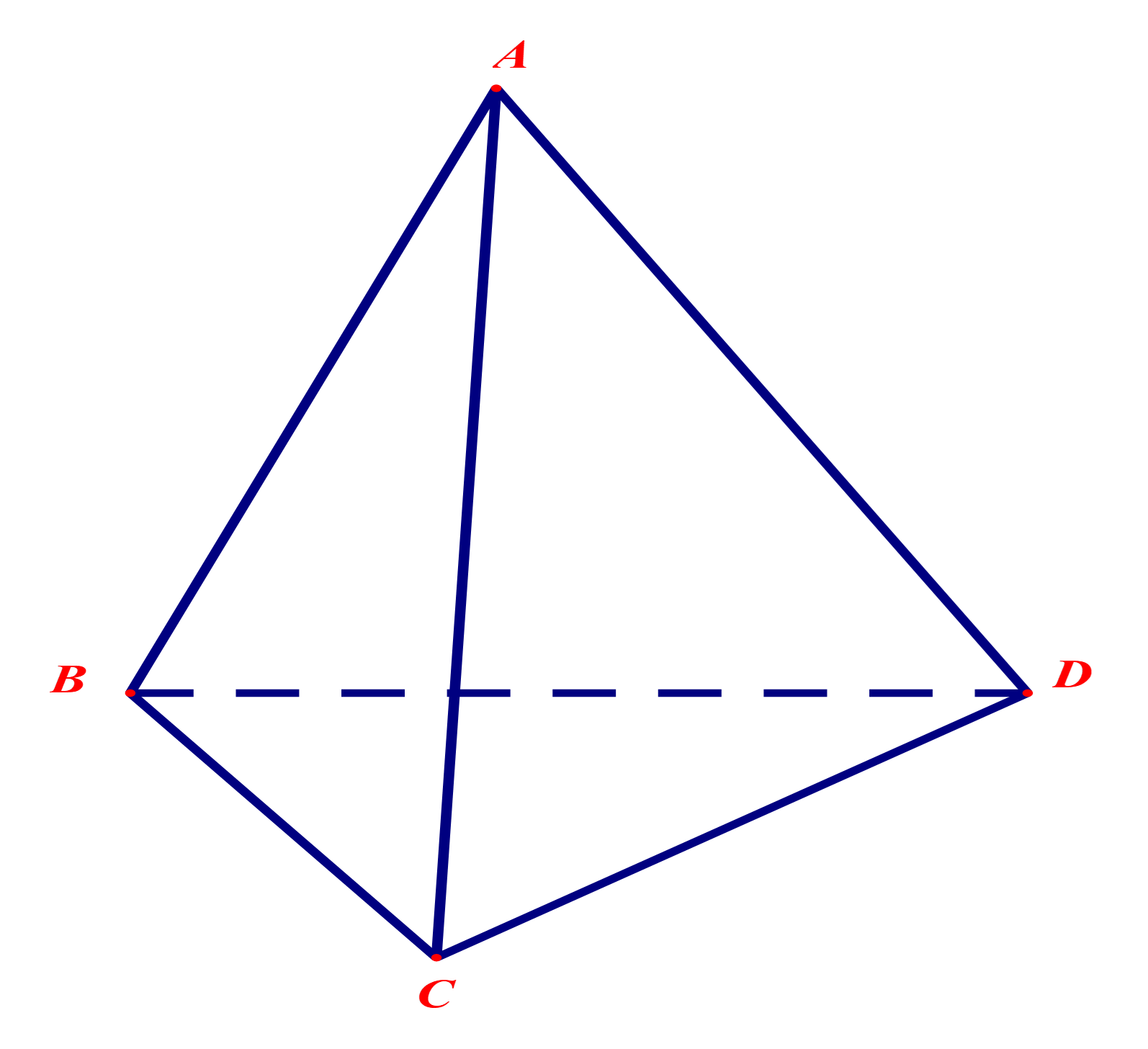
Hình nào dưới đây không phải là hình đa diện?
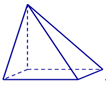
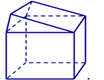
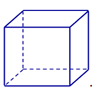
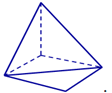
Hình 1 Hình 2 Hình 3 Hình 4
 Xem đáp án
Xem đáp án
Câu 38:
 Xem đáp án
Xem đáp án
Câu 39:
 Xem đáp án
Xem đáp án
Câu 40:
 Xem đáp án
Xem đáp án
Câu 41:
 Xem đáp án
Xem đáp án
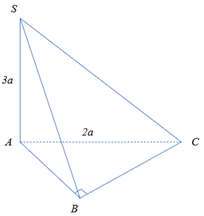
Câu 42:
 Xem đáp án
Xem đáp án
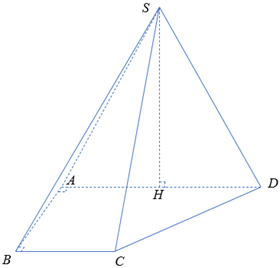
Câu 43:
 Xem đáp án
Xem đáp án
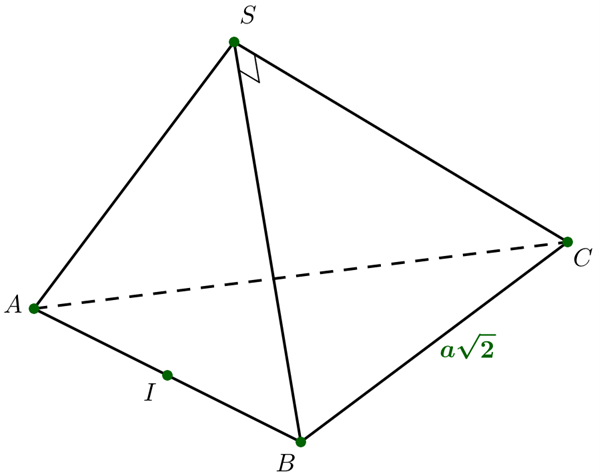
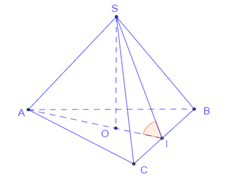
▪ Tam giác \(SBC\) là tam giác vuông cân tại \(S\), có \(BC = a\sqrt 2 \Rightarrow SB = SC = a\)\( \Rightarrow {S_{\Delta SBC}} = \frac{1}{2}.a.a = \frac{{{a^2}}}{2}\).
▪ Ta có: \({V_{A.SBC}} = \frac{1}{3}.\,{\rm{d}}\left( {A,\left( {SBC} \right)} \right).{{\rm{S}}_{\Delta SBC}} = {a^3}\)\( \Rightarrow \,{\rm{d}}\left( {A,\left( {SBC} \right)} \right) = \frac{{3{a^3}}}{{{{\rm{S}}_{\Delta SBC}}}} = \frac{{3{a^3}}}{{\frac{{{a^2}}}{2}}} = 6a\).
▪ Do \(I\) là trung điểm của \(AB\) nên \({\rm{d}}\left( {I,\left( {SBC} \right)} \right){\rm{ = }}\frac{1}{2}{\rm{d}}\left( {A,\left( {SBC} \right)} \right) = 3a\).
Câu 44:
 Xem đáp án
Xem đáp án
Câu 45:
 Xem đáp án
Xem đáp án
Câu 46:
 Xem đáp án
Xem đáp án
Câu 47:
 Xem đáp án
Xem đáp án
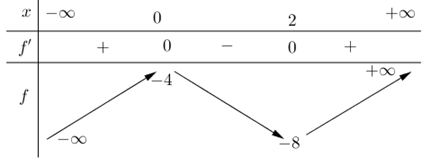
Lời giải
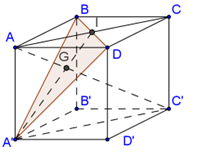
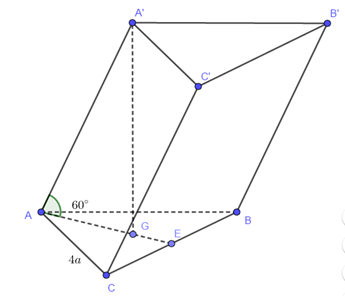
Gọi \(I\) là giao điểm của \(AC\) và \(BD.\)
Trong mặt phẳng \(\left( {ACC'A'} \right)\)\(AC'\) cắt \(A'I\) tại \(G.\)
Do \(AI\)song song \(A'C'\) và \(AI = \frac{1}{2}AC'\) nên \(IG = \frac{1}{2}GA'.\)
Suy ra \(G\) là trọng tâm tam giác \(A'BD\), mà tam giác \(A'BD\) đều (có các cạnh là các đường chéo của những hình vuông bằng nhau) nên \(GA' = GB = GD\) và \(AA' = AB = AD\) suy ra \(AG \bot (A'BD).\)
Do đó khoảng cách từ \(C'\)đến mặt phẳng \(\left( {A'BD} \right)\) là \(C'G.\)
Mặt khác \(C'G = \frac{2}{3}AC' = \frac{2}{3}AB\sqrt 3 = \frac{{4a\sqrt 3 }}{3} \Rightarrow AB = 2a.\) Vậy \(V = 8{a^3}.\)
Câu 48:
 Xem đáp án
Xem đáp án
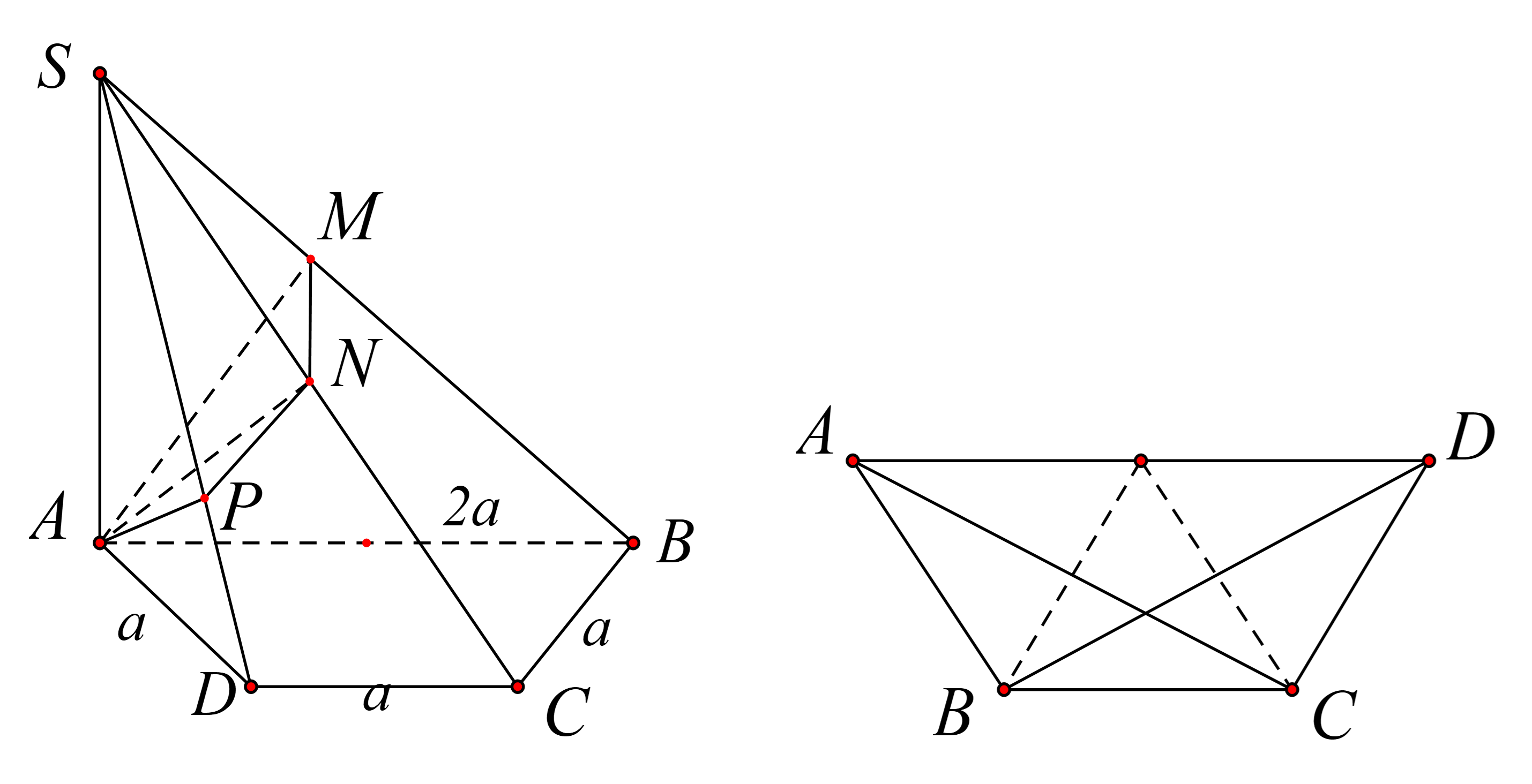
Câu 49:
 Xem đáp án
Xem đáp án
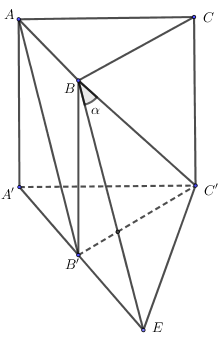
Câu 50:
 Xem đáp án
Xem đáp án