Lời giải
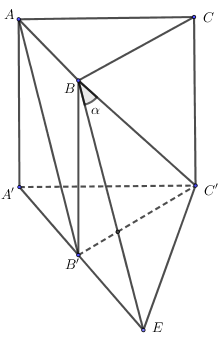
Gọi \(E\) là điểm đối xứng của \(A'\) qua \(B'\).
Ta có \(AB//B'E\) và \(AB = B'E = a\) suy ra \(ABEB'\) là hình bình hành.
\( \Rightarrow AB'//BE\)\( \Rightarrow \widehat {\left( {AB',BC'} \right)} = \widehat {\left( {BE,BC'} \right)} = \widehat {EBC'}\).
Xét tam giác \(BB'E\) có \(BB' \bot B'E\)\( \Rightarrow \)\(\Delta BB'E\) vuông tại \(B'\).
\( \Rightarrow BE = \sqrt {B{{B'}^2} + B'{E^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \).
Xét tam giác \(BB'C'\) có \(BB' \bot B'C'\)\( \Rightarrow \Delta BB'C'\) vuông tại \(B'\).
\( \Rightarrow BC' = \sqrt {B{{B'}^2} + B'{{C'}^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \).
Xét tam giác \(A'C'E\) có \(C'B' = A'B' = B'E = \frac{1}{2}A'E\).
\( \Rightarrow \Delta A'C'E\) vuông tại \(C'\)\( \Rightarrow C'E = \sqrt {A'{E^2} - A'{{C'}^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \).
Suy ra tam giác \(BEC'\) có \(BE = C'E = BC' = a\sqrt 3 \)\( \Rightarrow \Delta BEC'\) là tam giác đều.
\( \Rightarrow \widehat {EBC'} = 60^\circ \)\( \Rightarrow \widehat {\left( {AB',BC'} \right)} = 60^\circ \).
Vậy góc giữa đường thẳng \(AB'\) và \(BC'\) bằng \(60^\circ \).
Giải bởi Vietjack
