Giải bởi Vietjack
Giải bởi Vietjack
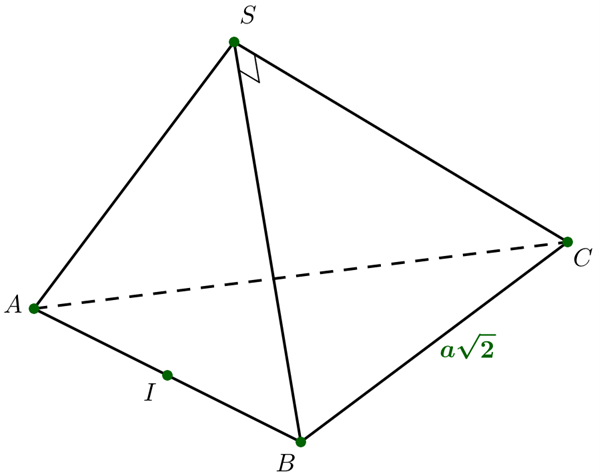
▪ Tam giác \(SBC\) là tam giác vuông cân tại \(S\), có \(BC = a\sqrt 2 \Rightarrow SB = SC = a\)\( \Rightarrow {S_{\Delta SBC}} = \frac{1}{2}.a.a = \frac{{{a^2}}}{2}\).
▪ Ta có: \({V_{A.SBC}} = \frac{1}{3}.\,{\rm{d}}\left( {A,\left( {SBC} \right)} \right).{{\rm{S}}_{\Delta SBC}} = {a^3}\)\( \Rightarrow \,{\rm{d}}\left( {A,\left( {SBC} \right)} \right) = \frac{{3{a^3}}}{{{{\rm{S}}_{\Delta SBC}}}} = \frac{{3{a^3}}}{{\frac{{{a^2}}}{2}}} = 6a\).
▪ Do \(I\) là trung điểm của \(AB\) nên \({\rm{d}}\left( {I,\left( {SBC} \right)} \right){\rm{ = }}\frac{1}{2}{\rm{d}}\left( {A,\left( {SBC} \right)} \right) = 3a\).
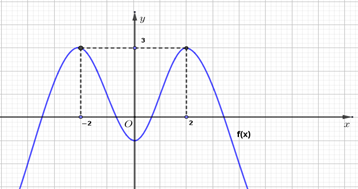
Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình vẽ: