Cho hàm số , (m là tham số thực). Tìm m để hàm số có cực đại, cực tiểu và ba điểm cực trị của đồ thị hàm số là ba đỉnh của một tam giác có bán kính đường tròn nội tiếp lớn hơn 1.
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có .
Hàm số có ![]() cực trị khi và chỉ khi phương trình có ba nghiệm phân biệt, điều này tương đương với m>0.
cực trị khi và chỉ khi phương trình có ba nghiệm phân biệt, điều này tương đương với m>0.
Khi đó tọa độ các điểm cực trị là .
Tam giác ABC cân tại A và gọi H là trung điểm của BC thì và do đó .
Ta có .
Suy ra .
.
Kết hợp với điều kiện suy ra .
Cho hàm số . Gọi M và m lần lượt là GTLN và GTNN của hàm số trên đoạn thì bằng:
Nếu tăng gấp hai lần chiều dài cạnh đáy của hình lăng trụ tứ giác đều thì thể tích tăng lên bao nhiêu lần?
Cho hàm số , hàm số liên tục trên R và có đồ thị như hình vẽ dưới đây:
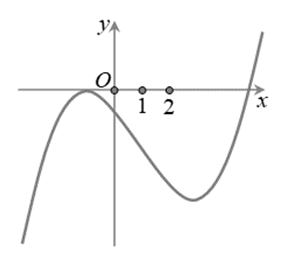
Tìm m để bất phương trình (m là tham số thực) nghiệm đúng với mọi .
Cho hàm số xác định, liên tục trên R và có bảng biến thiên như sau:
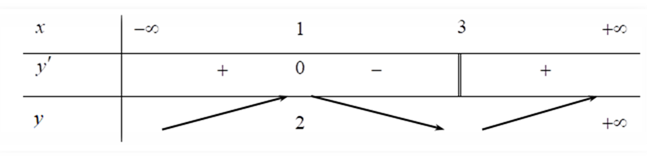
Khẳng định nào sau đây đúng?
Cho đồ thị hàm số y=f(x) có đồ thị như hình vẽ. Hàm số y=f(x) đồng biến trên khoảng nào dưới đây?
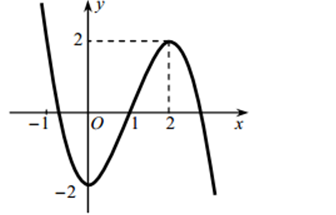
Tìm tất cả các giá trị thực của tham số m sao cho phương trình có đúng hai nghiệm thực phân biệt.