Cho hàm số y=f'(x-1) có đồ thị như hình vẽ: Tìm điểm cực tiểu của hàm số y=2f(x)-4x .
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: .
.
Đồ thị hàm số nhận được từ việc tịnh tiến đồ thị hàm số sang
trái 1 đơn vị.
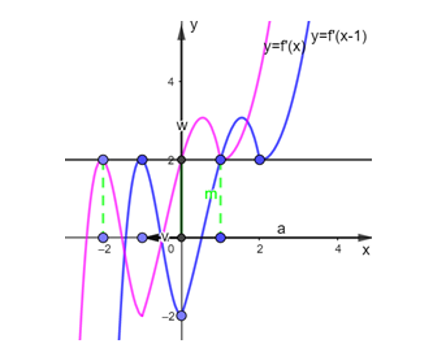
Nên .
Vì là các nghiệm bội chẵn nên ta có bảng biến thiên như sau:
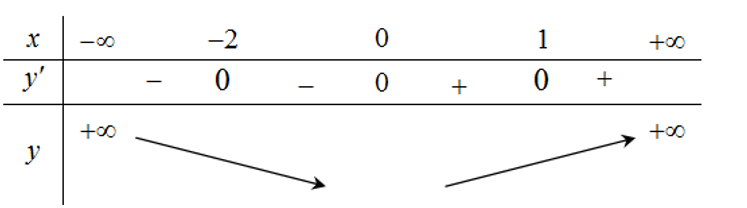
Từ bảng biến thiên suy ra hàm số đã cho điểm cực tiểu là x=0.
Cho hàm số f(x) . Hàm số y=f'(x) có đồ thị như hình bên. Hàm số g(x)=(1-2x)+-x nghịch biến trên khoảng nào ?
Cho hàm số liên tục trên R và có bảng xét dấu như sau
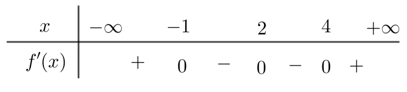
Hàm số có bao nhiêu điểm cực trị?
Cho hàm số có bảng biến thiên như sau:
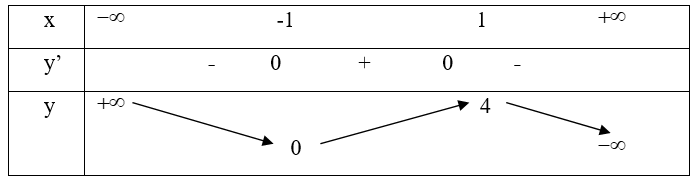
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Cho các hình sau:
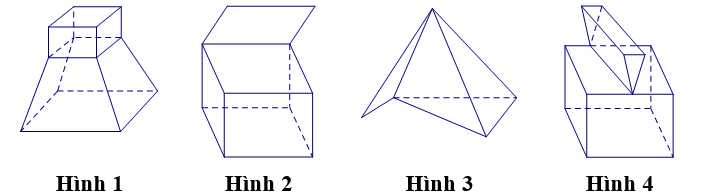
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
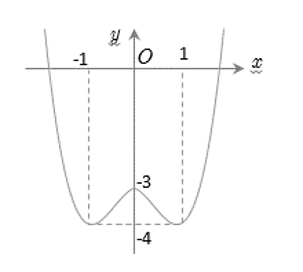
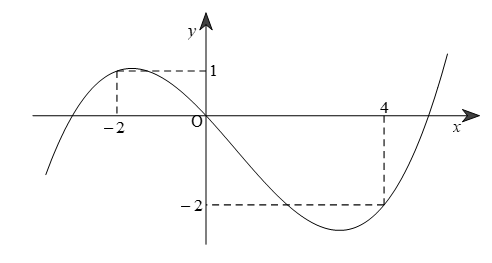
Cho hàm số y=f(x) có đồ thị là đường cong trong hình sau. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
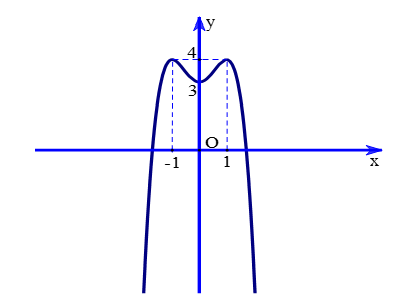
Cho hàm số bậc ba có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình là:
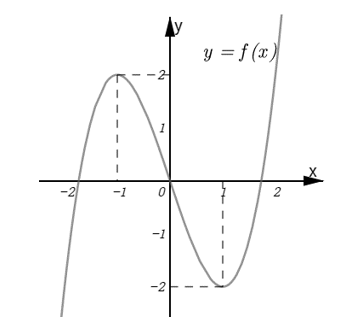
Cho hàm số xác định, liên tục trên R và có bảng biến thiên
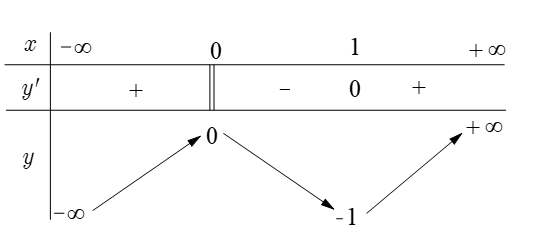
Khẳng định nào sau đây đúng?
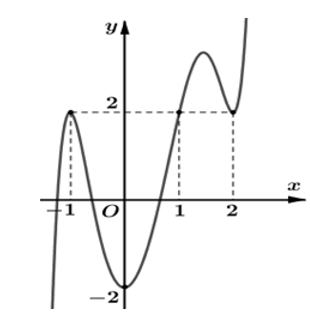
Cho hàm số y= f(x) có đồ thị như hình vẽ bên.
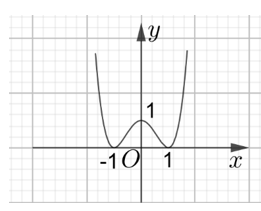
Số điểm cực trị của đồ thị hàm số y=f(x) là