Cho hàm số có đạo hàm . Hàm số liên tục trên tập số thực và có bảng biến thiên như sau:
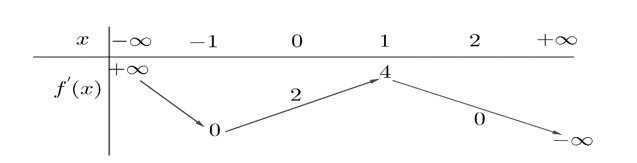
Biết rằng , . Tính giá trị nhỏ nhất của hàm số trên đoạn .
 Giải bởi Vietjack
Giải bởi Vietjack
Xét hàm số trên đoạn
, .
Từ bảng biến thiên, ta có:
Và , nên đồng biến trên
, nên vô nghiệm.
Do đó, chỉ có nghiệm là và x=-2 .
Ta có
.
Vậy .
Một tấm kẽm hình vuông ABCD có cạnh bằng 30 (cm) Người ta gập tấm kẽm theo hai cạnh EF và GH cho đến khi AD và BC trùng nhau như hình vẽ bên để được một hình lăng trụ hai đáy. Tìm x để thể tích khối lăng trụ lớn nhất.
Cho hàm số y=f(x) liên tục trên R, có đồ thị như sau
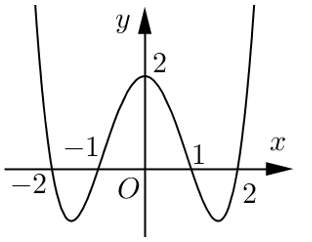
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
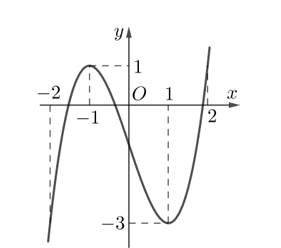
Cho hàm số y=f(x) xác định và liên tục trên R có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y=f(x) trên đoạn [-2,1].
![Cho hàm số y=f(x) xác định và liên tục trên R có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y=f(x) trên đoạn [-2,1]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/02/blobid0-1675871388.png)
Cho hàm số sao cho f'(x) có đồ thị như hình vẽ sau. Hàm số đạt cực đại tại điểm nào?
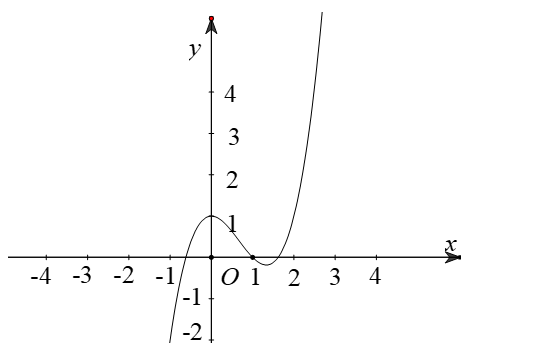
Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số này là
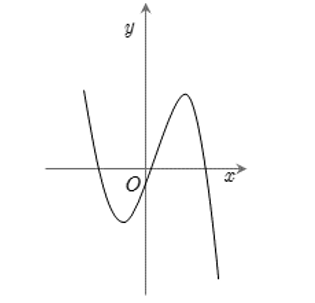
Cho hàm số . Có bao nhiêu giá trị nguyên của tham số m để hàm số không có điểm cực trị?
Cho hàm số có đồ thị như sau. Hàm số nghịch biến trên khoảng nào dưới đây?
Hai đường tiệm cận của đồ thị hàm số cùng với hai trục tọa độ tạo nên một hình chữ nhật có diện tích bằng bao nhiêu?
Thể tích khối chóp có chiều cao bằng h và diện tích đáy bằng B là