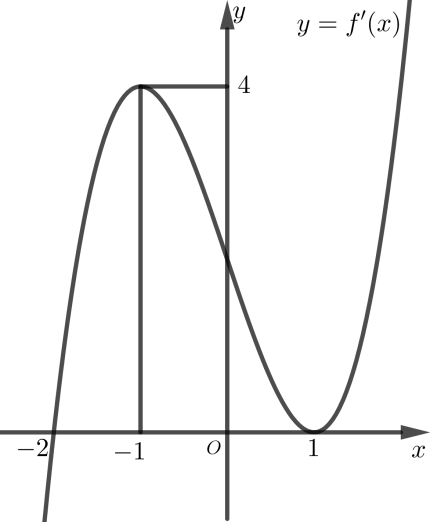
Lời giải
Chọn A
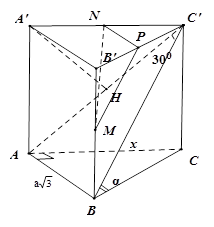
+) Ta có :\(\left( {BC',(AA'C'C)} \right) = \widehat {BC'A} = {30^0}\) và
\(\left( {BC',(ABC)} \right) = \widehat {C'BC} = \alpha \)
+) Đặt \(AB = x \Rightarrow BC = \sqrt {3{a^2} + {x^2}} \) ,
\(CC' = BC.\tan \alpha = \sqrt {\frac{{3({x^2} + 3{a^2})}}{5}} \)
\(AC' = AB.\cot {30^0} = x\sqrt 3 \)
Ta có : \(A{C^2} + CC{'^2} = AC{'^2} \Rightarrow x = a\sqrt 2 \Rightarrow CC' = a\sqrt 3 ,AC' = a\sqrt 6 \)
+) Gọi P là trung điểm của B’C’, suy ra:
\((MNP)//(ABC') \Rightarrow d(MN,AC') = d((MNP),(ABC')) = d(N,(ABC') = \frac{1}{2}d(A',(ABC')\)
Kẻ \(A'H \bot AC' \Rightarrow A'H \bot (ABC') \Rightarrow d(A',(ABC') = A'H = \frac{{AA'.A'C'}}{{AC'}} = \frac{{a\sqrt 6 }}{2}\)
Suy ra : \(d(MN,AC') = \frac{{a\sqrt 6 }}{4} \Rightarrow \) Đáp án A
Giải bởi Vietjack
