Tìm tất cả các giá trị thực của tham số m để hàm số không có cực đại.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
Ta có
Xét với m=1 : Khi đó hàm số không có cực đại. Vậy m=1 thỏa mãn (1)
Xét với : Khi đó hàm số là hàm bậc 4 trùng phương với hệ số để hàm số không có cực đại thì chỉ có một nghiệm duy nhất x=0 .
Hay vô nghiệm hoặc có nghiệm kép x=0 .
vô nghiệm hoặc có nghiệm x=0 (2)
Xét với : Hàm số bậc 4 trùng phương có hệ số luôn có cực đại (3)
Kết luận : Từ (1), (2), (3) ta có để hàm số không có cực đại thì .
Chọn đáp án A.
Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng a bằng
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a (tham khảo hình vẽ sau).
Thể tích của khối chóp đã cho bằng
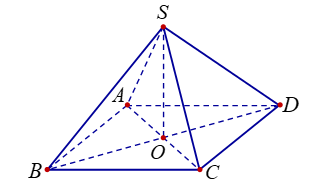
Xét khối chóp SABC có đáy là tam giác vuông cân tại A, SA vuông góc với mặt phẳng đáy, khoảng cách từ A đến mặt phẳng ( SBC) bằng 3. Gọi là góc giữa hai mặt phẳng ( SBC) và ( ABC), giá trị khi thể tích khối chóp SABC nhỏ nhất là
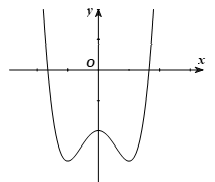
Cho hàm số bậc bốn Hàm số có đồ thị như hình vẽ dưới đây:
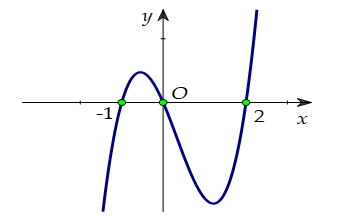
Hàm số đồng biến trên khoảng nào dưới đây?
Cho hình chóp có đáy là tam giác vuông tại vuông góc với đáy. Biết SC hợp với một góc thể tích của khối chóp bằng
Cho hàm số xác định trên , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
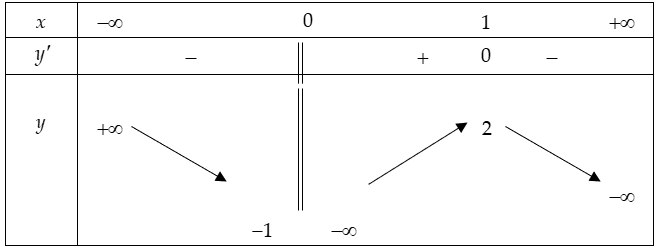
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình có ba nghiệm thực phân biệt.
Cho hàm số f(x) có đạo hàm , . Số điểm cực trị của hàm số đã cho là
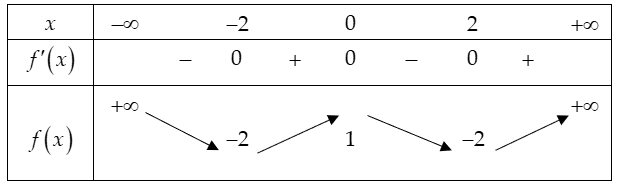
Cho hàm số có đồ thị như hình vẽ bên. Khẳng định nào dưới đây đúng?
Cho hàm số , bảng biến thiên của hàm số f'(x) như sau:

Số điểm cực trị của hàm số là
Một đoạn dây thép dài 200(cm) được uốn thành một chiếc khung có dạng như hình vẽ (hai đường cong là hai nữa đường tròn). Khi x thay đổi thì diện tích lớn nhất của hình phẳng thu được gần với giá trị nào sau đây?
Cho hàm số . Hàm số có đồ thị được cho ở hình vẽ dưới đây.
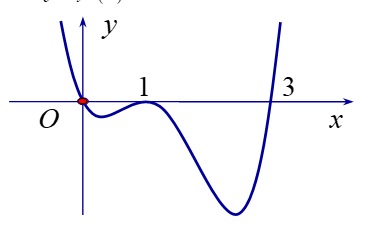
Có bao nhiêu giá trị nguyên của m để hàm số có 3 điểm cực trị?