Lời giải
Chọn A
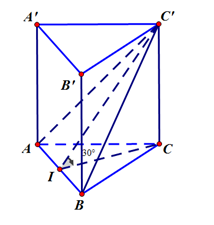
Gọi \(I\)là trung điểm của \(AB\), ta có \(\left\{ {\begin{array}{*{20}{l}}{AB \bot CI}\\{AB \bot CC'}\end{array} \Rightarrow AB \bot \left( {CIC'} \right)} \right.\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{AB = \left( {ABC} \right) \cap \left( {ABC'} \right)}\\{AB \bot \left( {CIC'} \right)}\\{\left( {CIC'} \right) \cap \left( {ABC} \right) = CI}\\{\left( {CIC'} \right) \cap \left( {ABC'} \right) = C'}\end{array}} \right.\) \( \Rightarrow \left( {\overline {\left( {ABC} \right),\left( {ABC'} \right)} } \right) = \left( {\widehat {CI,C'I}} \right) = \widehat {C'IC} = {30^^\circ }\).
Đặt \(AB = x(x > 0)\).
Vì \(CI\)là đường cao của tam giác đều \(ABC\)nên \(CI = \frac{{x\sqrt 3 }}{2}\).
+) \(CC' = CI \cdot {\rm{tan}}{30^^\circ } = \frac{{x\sqrt 3 }}{2} \cdot \frac{{\sqrt 3 }}{3} = \frac{x}{2}\), \(C'I = \frac{{CI}}{{{\rm{cos}}{{30}^^\circ }}} = x\).
Diện tích tam giác \(ABC'\) là \({S_{ABC'}} = \frac{1}{2}AB \cdot C'I \Leftrightarrow 8 = \frac{1}{2}{x^2} \Leftrightarrow x = 4\).
Thể tích khối lăng trụ đã cho là \(V = {S_{AQC}} \cdot CC' = \frac{{{x^2}\sqrt 3 }}{4} \cdot \frac{{x\sqrt 3 }}{2} \cdot {\rm{tan}}{30^^\circ } = \frac{{3{x^3}}}{8} \cdot \frac{{\sqrt 3 }}{3} = \frac{{{x^3}\sqrt 3 }}{8} = \frac{{{4^3}\sqrt 3 }}{8} = 8\sqrt 3 \).
Giải bởi Vietjack
là mặt phẳng đi qua điểm B và vuông góc với SC, chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó.
