Cho hình chóp có đáy ABCD là hình chữ nhật với và mặt bên SAD là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích lớn nhất của khối chóp .
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
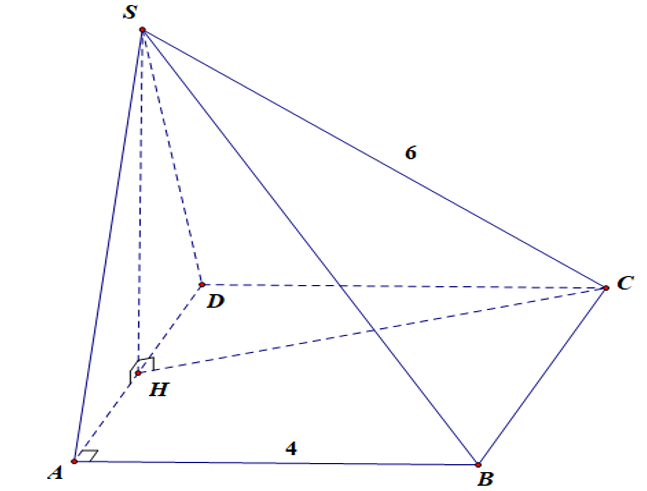
Gọi là trung điểm của . Theo giả thiết, suy ra .
Đặt . Suy ra
.
Suy ra (Bất đẳng thức Cauchy)
Cho hình lăng trụ ABCA'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và bằng . Tính thể tích V của khối lăng trụ .ABCA'B'C'
Trong các mệnh đề sau, mệnh đề nào sai?
A. Tồn tại khối lăng trụ đều là khối đa diện đều.
B. Tồn tại khối chóp tứ giác đều là khối đa diện đều.
C. Tồn tại khối tứ diện là khối đa diện đều.
D. Tồn tại khối hộp là khối đa diện đều.
Cho lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông tại B, , . Góc giữa cạnh A'B và mặt đáy là 60. Tính theo thể tích khối lăng trụ .
Gọi là giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị nằm trên các trục tọa độ. Mệnh đề nào sau đây đúng?
Cho tứ diện ABCD có DA=DC=DB , tam giác ABC vuông tại A. Chân đường cao của tứ diện xuất phát từ đỉnh D là điểm nào?
Cho hình chóp tam giác đều SABC có cạnh đáy bằng a và cạnh bên bằng . Tính theo a thể tích V của khối chóp SABC .
Hình vẽ bên là đồ thị hàm số trùng phương.
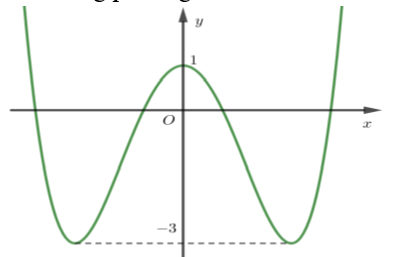
Tìm giá trị m để phương trình có bốn nghiệm phân biệt
Gọi là hai giá trị thực của tham số m để đồ thị hàm số có đúng một tiệm cận đứng. Tính