Đồ thị hàm số \(y = \frac{{\sqrt {1 - {x^2}} }}{{{x^2} + 2x}}\) có tất cả bao nhiêu tiệm cận đứng?
D. 0
Giải bởi Vietjack
Đáp án C
Phương pháp:
Cho hàm số \(y = f\left( x \right)\)
+) Nếu \(\mathop {\lim }\limits_{x \to \infty } y = {y_0} \Rightarrow y = {y_0}\) là đường TCN của đồ thị hàm số.
+) Nếu \(\mathop {\lim }\limits_{x \to {x_0}} y = \infty \Rightarrow x = {x_0}\) là đường TCĐ của đồ thị hàm số.
Cách giải:
Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l}1 - {x^2} \ge 0\\{x^2} + 2x \ne 0\end{array} \right. \Leftrightarrow x \in \left[ { - 1;1} \right]\backslash \left\{ 0 \right\}\)
\(\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty \Rightarrow \) đường thẳng \(x = 0\) là tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = 0;\,\,\,\mathop {\lim }\limits_{x \to {1^ - }} y = 0\)
Vậy hàm số đã cho có 1 tiệm cận đứng.
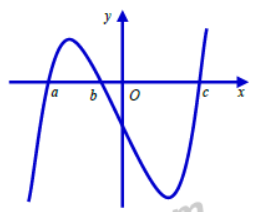
Cho hàm số \(y = f\left( x \right)\) có đạo hàm là hàm số liên tục trên R với đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ. Biết \(f\left( a \right) > 0\), hỏi đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = \left( {1 - m} \right){x^4} + 2\left( {m + 3} \right){x^2} + 1\) có đúng một điểm cực tiểu và không có điểm cực đại?
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 1\) trên đoạn \(\left[ {0;4} \right]\). Ta có \(m + 2M\) bằng:
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 1\) nghịch biến trên khoảng nào trong các khoảng sau đây?
Rút gọn biểu thức \(A = {a^{4{{\log }_{{a^2}}}3}}\) với \(0 < a \ne 1\) ta được kết quả là
Khoảng cách giữa hai điểm cực trị của đồ thị hàm số \(y = {x^3} + 3{x^2} - 4\) là
Số điểm chung của đồ thị hàm số \(y = {x^3} - 2{x^2} + x - 12\) với trục là Ox
Cho \(0 < a \ne 1\) và \(b \in R\). Chọn mệnh đề sai trong các mệnh đề sau:
Gọi \({m_0}\) là giá trị thực của tham số để đồ thị hàm số \(y = {x^4} + 2m{x^2} + 4\) có 3 điểm cực trị nằm trên các trục tọa độ. Khẳng định nào sau đây là đúng?
Rút gọn biểu thức \(A = \frac{{\sqrt[3]{{{a^5}}}.{a^{\frac{7}{3}}}}}{{{a^4}.\sqrt[7]{{{a^{ - 2}}}}}}\) với \(a > 0\) ta được kết quả \(A = {a^{\frac{m}{n}}}\), trong đó \(m,\,n \in \mathbb{N}*\) và \(\frac{m}{n}\) là phân số tối giản. Khẳng định nào sau đây đúng?
Giá trị lớn nhất của hàm số \(y = {x^3} - 3x + 5\) trên đoạn \(\left[ {0;\frac{3}{2}} \right]\)
Tìm tất cả các giá trị thực của x thỏa mãn đẳng thức \({\log _3}x = 3{\log _3}2 + {\log _9}25 - {\log _{\sqrt 3 }}3\)
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết \(OA = a,\,\,OB = 2a\) , và đường thẳng AC tạo với mặt phẳng \(\left( {OBC} \right)\) một góc \({60^0}\). Thể tích khối tứ diện OABC bằng
