D. \(R = \frac{a}{2}\)
Giải bởi Vietjack
Đáp án C
Phương pháp:
+) Xác định trục của mặt đáy (đường thẳng đi qua tâm đáy và vuông góc với đáy).
+) Xác định đường trung trực của một mặt bên.
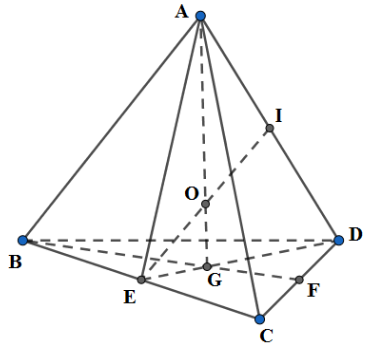
+) Xác định giao điểm của hai đường thẳng trên.
Cách giải:
Gọi E, F, I lần lượt là trung điểm của BC, CD, AD; G là trọng tâm tam giác BCD; O là giao điểm của AG và EI.
* Ta chứng minh: O là tâm mặt cầu ngoại tiếp tứ diện ABCD:
Thật vậy:
Do tam giác BCD đều, G là trọng tâm \( \Rightarrow \) là tâm đường tròn ngoại tiếp G
Do tứ diện ABCD đều \( \Rightarrow AG \bot \left( {BCD} \right)\)
Điểm \(O \in AG \Rightarrow OB = OC = OD\,\,\left( 1 \right)\)
Do \(AE = DE \Rightarrow \Delta AED\) cân tại E \( \Rightarrow \) EI là trung trực của AD \( \Rightarrow OA = OD\,\,\left( 2 \right)\)
Từ (1), (2) \( \Rightarrow \) O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
* Tính bán kính đường tròn ngoại tiếp tứ diện ABCD:
\(\Delta BCD\) đều, cạnh bằng a \( \Rightarrow ED = \frac{{a\sqrt 3 }}{2} \Rightarrow EG = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6},\,\,\,GD = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
\(\Delta EID\) vuông tại I \( \Rightarrow EI = \sqrt {E{D^2} - I{D^2}} = \sqrt {\frac{3}{4}{a^2} - \frac{1}{4}{a^2}} = \frac{1}{{\sqrt 2 }}a\)
\(\Delta OEG\) đồng dạng \(\Delta DEI \Rightarrow \frac{{OG}}{{ID}} = \frac{{EG}}{{EI}} \Leftrightarrow \frac{{OG}}{{\frac{a}{2}}} = \frac{{\frac{{a\sqrt 3 }}{3}}}{{\frac{1}{{\sqrt 2 }}a}} = \frac{{\sqrt 6 }}{3} \Rightarrow OG = \frac{a}{{\sqrt 6 }}\)
\(\Delta OGD\) vuông tại G \( \Rightarrow OD = \sqrt {O{G^2} + G{D^2}} = \sqrt {\frac{1}{6}{a^2} + \frac{1}{3}{a^2}} = \frac{a}{{\sqrt 2 }} = \frac{{a\sqrt 2 }}{4}\)
Vậy, bán kính đường tròn ngoại tiếp tứ diện ABCD là \(R = \frac{{a\sqrt 2 }}{4}\)
Hình nón \(\left( N \right)\) có thể tích bằng \(4\pi \) và chiều cao là 3. Tính bán kính đường tròn đáy của khối nón \(\left( N \right)\)
Cho \(a = {\log _2}m\) với \(m > 0,\,\,m \ne 1\). Đẳng thức nào dưới đây đúng?
Diện tích toàn phần của một hình hộp chữ nhật là \(S = 8{a^2}\). Đáy của hình hộp là hình vuông cạnh a. Tính thể tích V của khối hộp theo a.
Cho các số thực dương x, y, z thỏa mãn \(xy = {10^a},\,\,yz = {10^{2b}},\,\,xz = {10^{3c}}\,\,\left( {\,a,\,b,\,c \in \mathbb{R}} \right)\). Tính giá trị của biểu thức \(P = \log x + \log y + \log z\) theo a, b, c.
Gọi I là tâm đối xứng của đồ thị hàm số \(y = \frac{{2x - 3}}{{x + 2}}\). Tìm tọa độ điểm I.
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy là hình vuông cạnh bằng 3, đường chéo AB’ của mặt bên \(\left( {ABB'A'} \right)\) có độ dài bằng 5. Tính thể tích V của khối lăng trụ ABCD.A'B'C'D' .
Cho hàm số \(y = {x^4} - 2m{x^2} + 1\) có đồ thị \(\left( {{C_m}} \right)\). Tìm giá trị của m để đồ thị \(\left( {{C_m}} \right)\) có 3 điểm cực trị, đồng thời 3 điểm cực trị đó tạo thành một tam giác có diện tích bằng 4.
Cho hình nón có độ dài đường sinh là l, độ dài đường cao là h và r là bán kính đáy. Công thức tính diện tích xung quanh của hình nón.
Tìm tập các giá trị của tham số m để hàm số \(y = - {x^3} + 3m{x^2} - 3\left( {2m - 1} \right)x + 1\) có 2 điểm cực trị.
Cho hàm số \(y = {x^3} - x - 1\) có đồ thị \(\left( C \right)\). Viết phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung.
Cho khối nón đỉnh O trục OI, bán kính đáy bằng a và chiều cao bằng \(\frac{a}{2}\). Mặt phẳng \(\left( P \right)\) thay đổi luôn đi qua O và cắt hình nón theo thiết diện là tam giác AOB. Diện tích lớn nhất của tam giác AOB là:
Một người gửi tiết kiệm số tiền 100.000.000 VNĐ vào ngân hàng với lãi suất 8%/năm và lãi suất hàng năm được nhập vào vốn. Hỏi sau 15 năm số tiền người ấy nhận được về là bao nhiêu? (làm tròn đến đơn vị nghìn đồng).
Tìm đạo hàm của hàm số \(y = {\log _2}\left( {{e^x} + 1} \right)\)
