Thể tích của khối lăng trụ đều ABC.A’B’C’ biết cạnh đáy \[AB = a\], góc giữa A’B và mặt bên (ACC’A’) bằng \({45^0}\)
D. \(V = \frac{{{a^3}\sqrt 6 }}{{24}}\)
Giải bởi Vietjack
Đáp án A
Phương pháp:
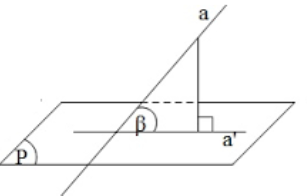
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
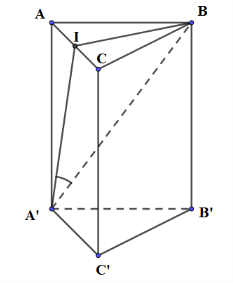
Gọi I là trung điểm của AC. \(\Delta ABC\) đều, \(AB = a \Rightarrow B = \frac{{a\sqrt 3 }}{2},\,\,\,{S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\) và \(BI \bot AC\)
Mà \(BI \bot AA'\left( {do\,AA' \bot \left( {ABC} \right)} \right)\)
\( \Rightarrow BI \bot \left( {ACC'A'} \right) \Rightarrow \left( {A'B;\left( {ACC'A'} \right)} \right) = \left( {A'B;A'I} \right) = IA'B = {45^0}\)
\(\Delta IA'B\) vuông tại I, \(IA'B = {45^0} \Rightarrow \Delta IA'B\) vuông cân tại I
\( \Rightarrow A'B = \sqrt 2 .IB = \sqrt 2 .\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{2}\)
\(\Delta ABA'\) vuông tại A \( \Rightarrow AA' = \sqrt {A'{B^2} - A{B^2}} = \sqrt {\left( {\frac{{a\sqrt 6 }}{2}} \right) - {a^2}} = \frac{{a\sqrt 2 }}{2}\)
Thể tích khối lăng trụ đều ABC.A’B’C’ là: \(V = {S_{ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 6 }}{8}\)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy, còn cạnh bên SC tạo với đáy mặt phẳng đáy một góc \({30^0}\). Thể tích của khối chóp đã cho là
Trong không gian, tập hợp các điểm M luôn cách đường thẳng d một khoảng không đổi R \[\left( {R > 0} \right)\] là
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, \(BC = a\sqrt 2 \), SC là đường cao, \(SC = a\). Mặt phẳng qua C, vuông góc với SB cắt SA, SB lần lượt tại E, F. Tính thể tích khối chóp S.CEF.
Giá trị nhỏ nhất m của hàm số \(y = \sqrt {5 - 4x} \) trên đoạn \(\left[ { - 1;1} \right]\) là:
Thể tích khối chóp tam giác có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy, biết \(AB = a,\,\,AC = 2a,\,\,SB = 3a\)
Tìm giá trị thực của tham số m để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - 4} \right)x + 3\) đạt cực tiểu tại \(x = 3\)
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc, \[AB = 2a,{\rm{ }}AC = 2a,{\rm{ }}AD = a.\] Bán kính mặt cầu ngoại tiếp tứ diện ABCD là R.
Thể tích của khối trụ (T) biết bán kính đáy r = 3, chiều cao h = 4 là
Viết biểu thức sau dưới dạng lũy thừa \(P = \sqrt x \sqrt[3]{{{x^2}}}\)
Rút gọn biểu thức \(P = {2^{{{\log }_2}a}} + {\log _3}{3^a}\) ta được kết quả là
Giá trị lớn nhất của hàm số \(y = - {x^4} + 4{x^2} + 2\) trên đoạn \(\left[ { - 2;2} \right]\) là
Tiếp tuyến của đồ thị hàm số \(y = {x^4} - 2{x^2} - 1\) tại điểm có hoành độ \({x_0} = 1\) là:
Cho mặt cầu (S) có bán kính R, hình trụ (H) có đường tròn hai đáy thuộc (S) và có chiều cao \(h = \frac{{2R}}{{\sqrt 3 }}\). Tính tỉ số thể tích \({V_1}\) của (H) và \({V_2}\) của (S).
