Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn A
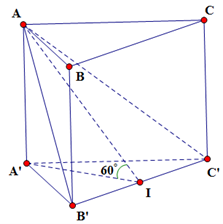
Gọi \[I\] là trung điểm \(B'C'\).
Góc giữa hai mặt phẳng \(\left( {AB'C'} \right)\) và \(\left( {A'B'C'} \right)\) là \(\widehat {AIA'}\) \( \Rightarrow \widehat {AIA'} = 60^\circ \)
\[AA' = A'I.\,tan60^\circ = \frac{{a\sqrt 3 }}{2}.\sqrt 3 = \frac{{3a}}{2}\].
\({V_{ABC.A'B'C'}}{\rm{ = }}AA'{\rm{.}}{{\rm{S}}_{A'B'C'}} = \frac{{3a}}{2}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{3{a^3}\sqrt 3 }}{8}\).