Cho tam giác ABC lấy M bất kì trên cạnh BC. Từ M kẻ đường song song với AB cắt AC tại D. Từ M kẻ đường thẳng song song với AC cắt AB tại E.
Chứng minh: ME = AD và MD = AE.
 Giải bởi Vietjack
Giải bởi Vietjack
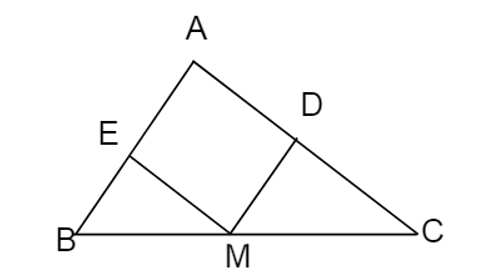
Xét tứ giác AEMD có : MD // AE (vì MD // AB) và ME // AD (vì ME // AC)
⇒ AEMD là hình bình hành. Theo tính chất của hình bình hánh ta suy ra được ME = AD và MD = AE (đpcm).
Cho tam giác ABC vuông góc tại A,có AB = AC.Gọi K là trung điểm của cạnh BC
a) Chứng minh tam giác AKB = tam giác AKC và AK vuông góc với BC.
b) Từ C kẻ đường thẳng vuông góc với BC, cắt AB tại E. Chứng minh EC song song với AK.
c) Chứng minh CE = CB.
Một trang trại cân thuê xe vận chuyển 450 con lợn và 35 tấn cám. Nơi cho thuê xe chỉ có 12 xe lớn và10 xe nhỏ. Một chiếc xe lớn có thể chở 50 con lợn và 5 tấn cám. Một chiếc xe nhỏ có thể chở 30 con lợn và 1 tấn cám. Tiền thuê một xe lớn là 4 triệu đồng, một xe nhỏ là 2 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thuê xe là thấp nhất?
Cho tam giác ABC vuông góc tại A,có AB = AC.Gọi K là trung điểm của cạnh BC
a) Chứng minh tam giác AKB = tam giác AKC và AK vuông góc với BC.
b) Từ C kẻ đường thẳng vuông góc với BC, cắt AB tại E. Chứng minh EC song song với AK.
c) Chứng minh CE = CB.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân đường vuông góc hạ từ H xuống AB và AC
a. CMR: ER = AH
b.Kẻ trung tuyến Am của tam giác ABC. C/m: AM⊥ EF
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH = 4cm và HC = 6cm.
a) Tính độ dài các đoạn AH, AB, AC
b) Gọi M là trung điểm của AC. Tính số đó góc AMB (làm tròn đến độ)
c) Kẻ AK vuông góc BM (K thuộc BM). Chứng minh:
Cho tam giác ABC đều. Gọi M, N lần lượt là các điểm trên cạnh AB, BC sao cho BM = BN. Gọi G là trọng tâm tam giác BMN và I là trung điểm của AN. Tính các góc của tam giác GIC.
Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
Cho tam giác ABC vuông tại A có M là trung điểm của BC
a) cho BC = 10cm tính AM
b) gọi N là trung điểm của AB cho MN // AC
c) kẻ MD // AD chứng minh tứ giác ANMD là hình chữ nhật
Cho tam giác ABC vuông tại A, có AB < AC, trên cạnh BC lấy điểm D sao cho BD = BA. Kẻ AH vuông góc BC, DK vuông góc AC.
a) C/m góc BAD = góc BDA
b) C/m AD là phân giác của góc HAC
c) C/m AK = AH
d) C/m AB + AC < BC + AH
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân đường vuông góc hạ từ H xuống AB và AC
a. CMR: ER = AH
b.Kẻ trung tuyến Am của tam giác ABC. C/m: AM⊥ EF