Giải bởi Vietjack
Giải bởi Vietjack
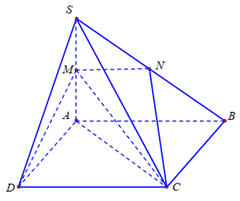
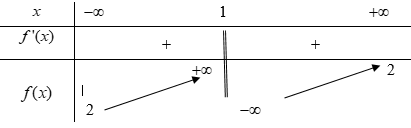
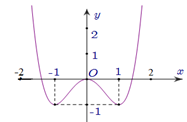
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ bên
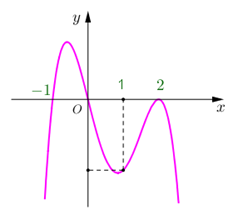
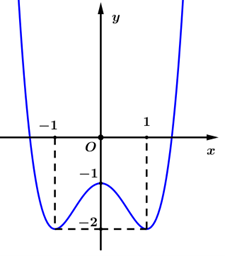
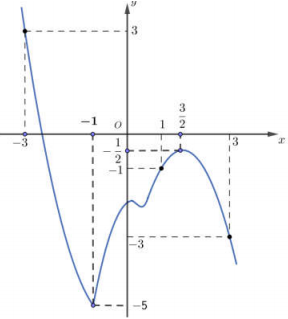
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(f'\left( x \right)\) như hình vẽ
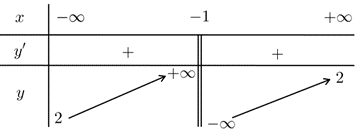
Cho hàm số \(y = \frac{{ax + b}}{{cx + 1}}\,\,\left( {a\,,b\,,c \in \mathbb{R}} \right)\)có bảng biến thiên như sau: